Соответствие методов и множеств

Основные понятия.

Литература к лекции 1.

1.М.А. Королев, Т.Ю. Крупкина, М.А. Ревелева. Технология, конструкции и методы моделирования кремниевых интегральных микросхем. Часть 1. М.: БИНОМ. Лаборатория знаний. 2007. 397с.

Дополнительная литература

Черняев В.Н. Технология производства интегральных микросхем и микропроцессоров.М.: Радио и связь, 1987.

2. Броудай И., Мерей Д. Физические основы микротехнологии. - М.: Мир, 1985.

4. Ефимов И.Е., Козырь И.Я., Горбунов Ю.И. Микроэлектроника. Физические и технологические основы, надежность: Учеб. пособие для прибостроит. спец. вузов / М.; Высш. шк., 1986 г.

5. Коледов Л.А. Технология и конструкции микросхем, микропрорцессоров и микросборок: Учебник для вузов / М.: Радио и связь, 1989 г

1. X - множество вариантов или допустимое множество.

2. f: X®R₁ ­ - целевая функция.

3. Точка x*ÎX - оптимальная, если выполняется f(x*)=min f(x), xÎX (­­*).

Если верно (*) для любого xÎX, то точка x- точка глобального минимума.

Если нет, но существует eÎR₁, e >0 такое что:

f(x) ³ f(x*),для любого x из e- окрестности, то есть ||x-x*||<e, то

x* - точка локального минимума.

Надо найти экстремумы функции f на множестве X.

Содержание курса состоит в поисках экстремумов.

Будем искать min f(x), xÎX, так как max f(x)= - min(-f(x)), xÎX.

Множество X бывает:

1. Конечным (конечное множество элементов, например графы).

2. Конечномерным (когда совпадает или является подмножеством множества евклидова пространства).

3. Бесконечномерным (не вкладывается в евклидово пространство,например множество непрерывных функций на отрезке).

1. Методы решения переборных задач (метод ветвей и границ, динамическое

программирование и др.)

2. Методы решения задач математического программирования

(условная/безусловная минимизация, нелинейное, выпуклое и линейное

программирование).

3. Методы вариационного исчисления и методы оптимального управления

(уравнение Эйлера-Лагранжа, принцип максимума).

I. Безусловная оптимизация ( многомерные функции).

min f(x), x = R­ⁿ, то есть минимизация на всем пространстве.

Определение:

Минимизация заданная неравенствами, равенствами и другими ограничениями называется условной.

Пусть:

1. x = Rⁿ (евклидово n-мерное пространство);

2. Функция f дифференцируема хотя бы один раз,

тогда в точке минимума выполняется равенство:

Ñf(x)=0, где

(вектор частных производных по каждому аргументу)

Ñf(x)=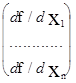

В большинстве случаев это приводит к решению системы нелинейных уравнений, что само по себе проблема. Существуют релаксационные методы, в основе которых лежит построение релаксационной последовательности со следующими свойствами:

1) x_iÎX,"i;

2) f(x₀)>f(x₁)>...;

3) x_i®x* = argmin f(x), i®¥, xÎX.

Это методы нахождения локального минимума (т.е. корня уравнения Ñf(x) =0). Все рассматриваемые методы делятся на несколько групп в зависимости от того, какой максимальный порядок производной функции f используется для вычисления последовательности. Если производные не используются, то методы нулевого порядка, затем -первого и так далее. Мы будем рассматривать порядок не выше второго.

Общая схема безусловной оптимизации

xÎR_n

x_k+1 = x_k+ t_kS_k, где S_k - вектор, определяющий направление изменения x_k

t_k - скаляр, определяющий длину шага.

S_k может зависеть от xk: Sk = j(x_k), а может от x_k-1.В зависимости от этого критические методы делятся на:

n одношаговые (j(x_k));

n двухшаговые (j(x_k,x_k+1)).

Эти методы имеют основное распространение.