Неравенство мощностей

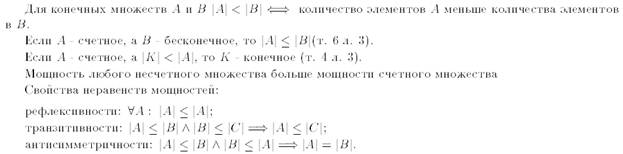
Отношение " иметь не большую мощность" обладает свойствами:

• Если и равномощны, то имеет не большую мощность, чем . (Очевидно.)
• Если имеет не большую мощность, чем , а имеет не большую мощность, чем 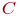, то имеет не большую мощность, чем 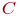. (Пусть находится во взаимно однозначном соответствии с 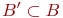, а находится во взаимно однозначном соответствии с 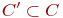. Тогда при втором соответствии 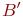соответствует некоторому множеству , как показано на рис, и потому равномощно .)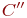

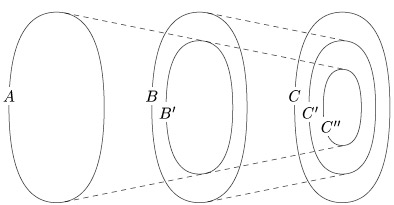
Рис. Транзитивность сравнения мощностей

• Если имеет не большую мощность, чем , а имеет не большую мощность, чем , то они равномощны. (Это утверждение составляет содержание теоремы Кантора - Бернштейна)
• Для любых двух множеств и верно (хотя бы) одно из двух: либо имеет не большую мощность, чем , либо имеет не большую мощность, чем .

Теорема. (Кантора-Бернштейна) Если множество равномощно некоторому подмножеству множества , а равномощно некоторому подмножеству множества , то множества и равномощны.