2014-02-09
1358
Можно считать, что 
не пересекается с 
(пересечение можно выбросить из , останется по-прежнему конечное или счетное множество).
Выделим в счетное подмножество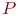 
; остаток обозначим через 
. Тогда нам надо доказать, что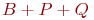 
равномощно 
(знак 
символизирует объединение непересекающихся множеств). Поскольку 
и 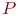оба счетны, между ними существует взаимно однозначное соответствие. Его легко продолжить до соответствия между 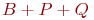и (каждый элемент множества соответствует сам себе).
