Спектр колебания при гармонической угловой модуляции

Пусть заданно колебание

(9.22)

о котором известно, что передаточное сообщение заложено в функцию .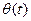

Если колебание 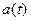получено с помощью ФМ, то 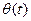и S(t) полностью совпадают по форме и отличаются лишь постоянным коэффициентом. При этом, очевидно, точностью до постоянного коэффициента совпадают и спектры функций 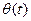и S(t).

При ЧМ функция 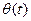является интегралом от передаваемого сообщения S(t). Это вытекает из (9.16) и (9.17). так как интегрирование является линейным преобразованием, то при ЧМ спектр функции 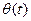состоит из тех же компонентом, что и спектр сообщения S(t), но с измененными амплитудами и фазами.

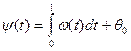, (9.16)

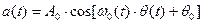. (9.17)

Отвлекаясь от способа осуществления угловой модуляции (фазовой или частотной) и считая заданным спектр функции 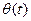, найдем спектр модулированного колебания a(t):

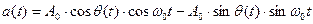. (9.23)

Таким образом, модулированное по углу колебание можно рассматривать как сумму двух квадратурных колебаний:

косинусного и

синусного .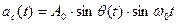

При гармонической уг8ловой модуляции 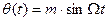, тогда

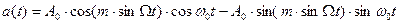. (9.24)

Из теоремы Бесселелевых функций известны следующие соотношения:

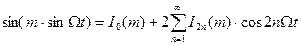где 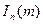- Бесселева функция первого рода n -го порядка от аргумента m.

После подстановки 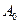и преобразований получим для a(t):

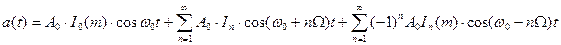. (9.25)

То есть, при синусоидальных ЧМ и ФМ имеем безграничный спектр, который состоит из спектральной линии «несущей» 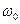и двух боковых полос .

Амплитуда несущей - 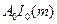, при значениях m=2.3;5.4 пренебрежимо мала, а амплитуды боковых частот 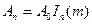зависит от значения аргумента m Бесселовой функции.

При n>m – составляющие спектра малы и ими можно пренебречь.

Практически ширина спектра при угловой модуляции равна:

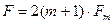, (9.26)

где 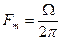- частота модулирующего колебания.

Количество значимых спектральных линий в спектре a(t) можно определить по формуле:

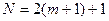, (9.27)

m – индекс угловой модуляции: .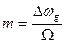

При m>>1 ширину спектра можно определить по формуле:

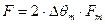. (9.28)

При ЧМ девиация 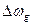пропорциональна амплитуде модулирующего сигнала S(t) и не зависит от 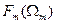, а при ФМ, ее индекс 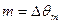пропорционален амплитуде s(t), независимо от его частоты, поэтому девиация частоты при ФМ линейно увеличивается с ростом 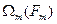. При ЧМ обычно применяется прямое воздействие на частоту 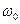генератора несущей, а при ФМ – генератор имеет стабильную частоту 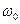, а фаза колебания модулируется в одном из последующих каскадов передатчика.