Схема фильтрации
Схема компенсации
ОСНОВНЫЕ АЛГОРИТМЫ ОБРАБОТКИ ИНФОРМАЦИИ В ПНК
ЛЕКЦИЯ №3
Основными задачами ПНК с точки зрения источника информационного обеспечения ЛА является:
· обобщенная обработка навигационной информации, которая поступает на борт ЛА;
· обеспечение высокой надежности функционирования бортовых систем и комплексов ЛА, и в итоге безопасность полета, за счет резервирования источников информации.
К основным методам обработки информации в ПНК относятся оптимальная фильтрация и оптимальное управление, реализуемые в современных ПНК. Наилучших результатов повышения качественных характеристик измерительных комплексов достигается в системах со структурной избыточностью, и применением методов комплексирования.
В современных ПНК широкое распространение получили такие способы суммарной обработки однородной информации, которая поступает от нескольких измерителей:
· взаимная компенсация и фильтрация ошибок измерительных приборов, измеряющих один и тот же параметр;
· оптимальная оценка вектора состояния с использованием априорной информации о контролируемом процессе и текущие измерения, которые реализуют алгоритм оптимальной фильтрации Калмана.
Предположим, один и тот же навигационный параметр измеряется двумя или несколькими измерителями, выполненными на различных физических принципах. Тогда алгоритм компенсации, позволяющий снизить погрешность измерения данного навигационного параметра, может быть реализован согласно схеме:
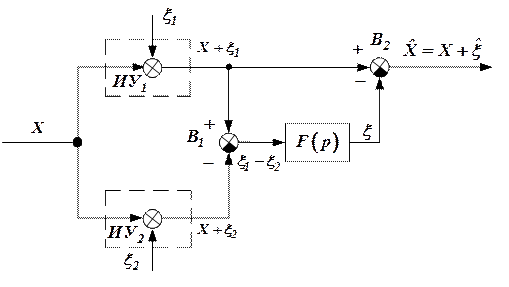
Рисунок 1
Сигналы измерительных устройств  , и
, и  кроме измеряемой величины
кроме измеряемой величины 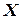 содержат в себе сигналы ошибок
содержат в себе сигналы ошибок  ,
,  и поступают на вход вычитателя
и поступают на вход вычитателя  . На входе
. На входе  формируется сигнал
формируется сигнал
 .
.
Сигнал 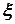 пропускается через динамический фильтр
пропускается через динамический фильтр 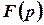 и поступает на вход вычитателя
и поступает на вход вычитателя  , на выходе которого имеем
, на выходе которого имеем

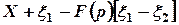
или
 ,
,
где  - ошибка комплексной системы.
- ошибка комплексной системы.
Обычно фильтр низких частот в простейшем случае представляет собой апериодическое звено:
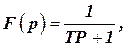 | (1) |
где  - постоянная времени.
- постоянная времени.
Передаточная функция фильтра высоких частот
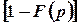  | (2) |
практически представляет собой реальное дифференцирующее звено.
С учетом передаточных функций фильтров (1) и (2) исходная схема (рис.1) для получения  представлена на рис. 2.
представлена на рис. 2.
Учитывая прогнозируемый характер спектральных характеристик  и
и  - спектральных плотностей
- спектральных плотностей 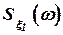 и
и  (рис. 3), можно показать графики спектральных характеристик сигналов ошибок
(рис. 3), можно показать графики спектральных характеристик сигналов ошибок  и
и 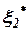 в виде дисперсий ошибок
в виде дисперсий ошибок 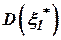 и
и  , полученных в результате прохождения сигналов через соответствующие фильтры с амплитудно-частотными характеристиками (АЧХ)
, полученных в результате прохождения сигналов через соответствующие фильтры с амплитудно-частотными характеристиками (АЧХ)  и
и  .
.
 ; ; | (3) |
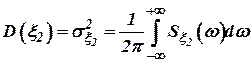 , , | (4) |
где  ,
,  - среднеквадратические ошибки выходных сигналов.
- среднеквадратические ошибки выходных сигналов.
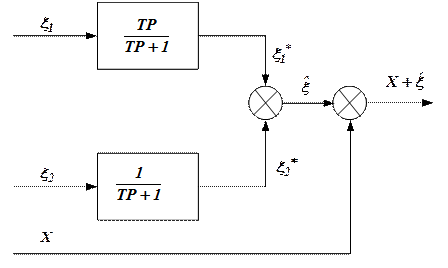
Рисунок 2
Спектральная плотность  для функции
для функции  определяется с помощью соотношения Хинчина-Винера.
определяется с помощью соотношения Хинчина-Винера.
 , , |
где 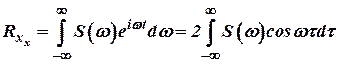 .
.
В свою очередь функция  .
.
Если , то
, то .
.
Дисперсия ошибки системы при реализации способа компенсации имеет вид:
 . . | (5) |
На основании рис. 3 можно сделать вывод о том, что дисперсия ошибки системы тем меньше, чем больше отличаются частотой спектральные плотности ошибок входных сигналов. Таким образом, задача комплексирования двух измерителей состоит в выборе такой частотной характеристики фильтра  , чтобы после суммирования сигналов (см. рис. 2), параметр на выходе схемы
, чтобы после суммирования сигналов (см. рис. 2), параметр на выходе схемы  был близок к измеряемому параметру
был близок к измеряемому параметру  .
.
 Рисунок 3
Рисунок 3
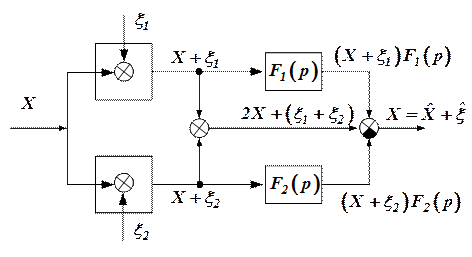
Схему компенсации можно реализовать, используя схему с обратной связью (рис. 4). Уравнение ошибок в этом случае эквивалентно полученным ранее для схемы компенсации без обратной связи (см. рис. 1).
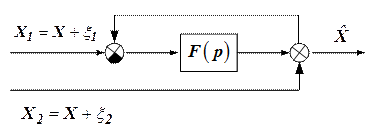
Рисунок 4
Для схемы компенсации, изображенной на рис. 4 можно записать:
 , , | (6) |
откуда имеем
 , , | (7) |
где
 . . | (8) |
Если  , то уравнение ошибок полностью совпадает.
, то уравнение ошибок полностью совпадает.
Пусть 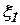 - низкочастотная помеха,
- низкочастотная помеха, 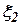 - высокочастотная помеха.
- высокочастотная помеха.
Низкочастотный фильтр -  ;
;
Высокочастотный фильтр - 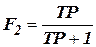 .
.
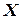 =
= =
=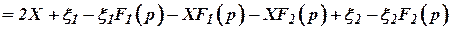 =
=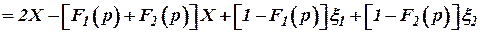 =
= =
= ,
,
где  , то есть в данном случае динамические фильтры не пропускают соответственно на выход высокочастотную помеху
, то есть в данном случае динамические фильтры не пропускают соответственно на выход высокочастотную помеху , то есть она не может пройти через низкочастотный динамический фильтр
, то есть она не может пройти через низкочастотный динамический фильтр  и наоборот фильтр
и наоборот фильтр  не пропускает низкочастотную составляющую помеху
не пропускает низкочастотную составляющую помеху  .
.
Схема фильтрации в случае, когда один и тот же параметр измеряется двумя измерителями, имеет вид, представленный на рис. 5.
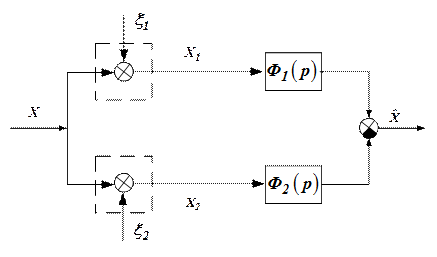
Рисунок 5
Сигнал на выходе такой системы описывается уравнением:
 | (9) |
или
 . . | (10) |
Для того, чтобы система не вносила динамических ошибок, необходимо выполнять условие:
 . . | (11) |
В этом случае выходной сигнал имеет вид
 , , | (12) |
где  .
.
Таким образом, при  выражение (12) превращается в выражение (1), что свидетельствует об эквивалентности схем компенсации и фильтрации.
выражение (12) превращается в выражение (1), что свидетельствует об эквивалентности схем компенсации и фильтрации.
Рассмотрим параметрический синтез комплексной системы измерения высоты, которая использует сигнал от радиовысотомера и баровысотомера.
Радиовысотомер имеет стационарную флуктуационную ошибку  , описываемую корреляционной функцией:
, описываемую корреляционной функцией:
 . . | (13) |
Барометрический высотомер кроме стационарной флуктуационной составляющей ошибки  , которая описывается корреляционной функцией
, которая описывается корреляционной функцией
 , , | (14) |
имеют регуляторную нестационарную составляющую
 , , | (15) |
где  - центрированная случайная величина с заданной дисперсией
- центрированная случайная величина с заданной дисперсией  .
.
Таким образов
 . . | (16) |
Спектр флуктуационной ошибки радиовысотомера значительно шире спектра аналогичной ошибки баровысотомера ( ), поэтому для реализации комплексной системы измерения высоты рационально выбрать схему с фильтром сигнала равной разнице сигналов на низкой частоте, то есть обработку информации измерителей осуществлять согласно схеме компенсации, изображенной на рис. 6.
), поэтому для реализации комплексной системы измерения высоты рационально выбрать схему с фильтром сигнала равной разнице сигналов на низкой частоте, то есть обработку информации измерителей осуществлять согласно схеме компенсации, изображенной на рис. 6.
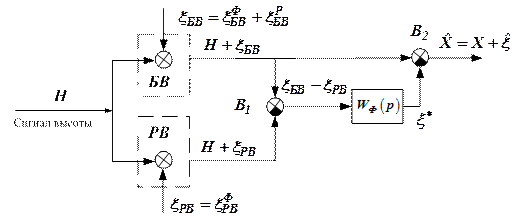
Рисунок 6
Вид передаточной функции фильтра, с целью выделения регуляторной составляющей ошибки баровысотомера, определяется из условий обеспечения астатизма первого порядка, то есть:
 , , | (17) |
где постоянная времени  определяется из условий минимизации среднеквадратической ошибки комплексной системы.
определяется из условий минимизации среднеквадратической ошибки комплексной системы.
В данном случае параметрическую минимизацию удобнее проводить в частотной области. Переходя к спектральным характеристикам ошибок, имеет выражение для спектральной плотности РВ:
 , , | (18) |
аналогично спектральная плотность БВ:
 . . | (19) |
С учетом того, что  , спектр ошибки радиовысотомера в полосе пропускания фильтра низких частот практически постоянный и равняется значению спектральной плотности при
, спектр ошибки радиовысотомера в полосе пропускания фильтра низких частот практически постоянный и равняется значению спектральной плотности при 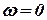 .
.
 . . | (20) |
Таким образом, ошибку радиовысотомера можно считать белым шумом.
Составляющие ошибки комплексной системы 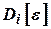 с учетом ошибок отдельных измерителей имеет вид
с учетом ошибок отдельных измерителей имеет вид
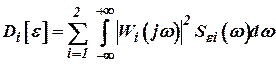 , ,  . . | (21) |
Передаточная функция фильтра для сигнала  равна
равна  , и в таком случае автоматически выполняются условия инвариантности при будь каких параметрах фильтра
, и в таком случае автоматически выполняются условия инвариантности при будь каких параметрах фильтра  . Соответственно дисперсии ошибок БВ и РВ в соответствии с формулой (21) имеем
. Соответственно дисперсии ошибок БВ и РВ в соответствии с формулой (21) имеем
 ; ; | (22) |
 . . | (23) |
Дисперсия ошибки комплексной системы с учетом независимости ошибок измерителей определяется как
 . . | (24) |
Выражение (24) является целевой функцией, которую необходимо минимизировать относительно параметра  . Ограничением на параметр
. Ограничением на параметр  есть только его позитивность.
есть только его позитивность.
Обозначим:
 ; ;  . . | (25) |
Тогда с учетом (25) выражение (24) представим как:
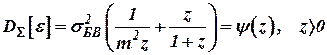 . . | (26) |
Минимум функции  определяется из условия
определяется из условия
 . . | (27) |
После дифференцирования (26) и приравнивания 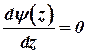 имеем квадратичное уравнение
имеем квадратичное уравнение
 , , |
откуда
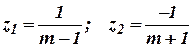 . . |
Значение  не удовлетворяет условию
не удовлетворяет условию 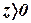 , то есть позитивности
, то есть позитивности  . При
. При  ,
,  также
также  , что выполнятся, так как
, что выполнятся, так как  и
и  имеют один порядок, а
имеют один порядок, а  . Таким образом, решением (27) является
. Таким образом, решением (27) является  .
.
Исследуя условия для  , получим
, получим
 , , |
то есть  , действительно определяет минимум функции
, действительно определяет минимум функции  , заданной формулой (26).
, заданной формулой (26).
Оптимальное значение постоянной времени  определяется в виде
определяется в виде
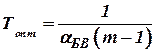 .
.
 2014-02-09
2014-02-09 948
948








