ЗАМЕЧАНИЕ Уравнение окружности можно задать и в параметрическом виде
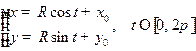 , в чем нетрудно убедиться подстановкой в предыдущее уравнение.
, в чем нетрудно убедиться подстановкой в предыдущее уравнение.
Опредление Эллипс – множество точек в 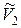 , сумма расстояний от каждой и которых до двух заданных точек (фокусов) есть величина постоянная.
, сумма расстояний от каждой и которых до двух заданных точек (фокусов) есть величина постоянная.
ЗАМЕЧАНИЕ 1 Фиксируем ПДСК в 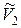 . Обозначим сумму расстояний до фокусов
. Обозначим сумму расстояний до фокусов 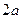 , и расположим фокусы на оси
, и расположим фокусы на оси 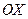 симметрично относительно начала координат:
симметрично относительно начала координат:  .
.
Положим 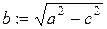 . Тогда уравнение эллипса (каноническое) будет иметь вид
. Тогда уравнение эллипса (каноническое) будет иметь вид
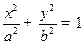 .
.
ЗАМЕЧАНИЕ 2 В каноническом уравнении эллипса предполагается 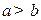 ; отрезки
; отрезки 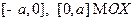 называются большими полуосями, а отрезки
называются большими полуосями, а отрезки 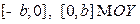 - малыми полуосями эллипса.
- малыми полуосями эллипса.
Определение Эксцентриситетом эллипса называется величина
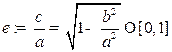 .
.
ЗАМЕЧАНИЕ 3 (геометрический смысл) Если 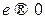 при фиксированном
при фиксированном 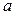 , то эллипс деформируется к окружности
, то эллипс деформируется к окружности 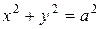 . Если
. Если 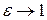 , то эллипс деформируется к отрезку
, то эллипс деформируется к отрезку 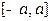 .
.
Определение Прямая 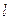 , проходящая через точку
, проходящая через точку 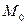 кривой, называется касательной к кривой в этой точке, если расстояние от переменной точки кривой
кривой, называется касательной к кривой в этой точке, если расстояние от переменной точки кривой 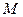 до прямой стремится к нулю быстрее, чем расстояние от нее до
до прямой стремится к нулю быстрее, чем расстояние от нее до 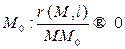 , когда
, когда 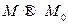 .
.
ЗАМЕЧАНИЕ 4 Уравнение касательной к эллипсу в точке 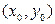 имеет вид
имеет вид 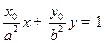 .
.
_____
Определение Гипербола – множество точек в 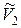 , модуль разности расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная.
, модуль разности расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная.
ЗАМЕЧАНИЕ 1 Пусть модуль разности расстояний от текущей точки 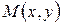 гиперболы до фокусов
гиперболы до фокусов  равен
равен 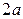 :
: 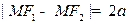 .Тогда уравнение гиперболы (каноническое) имеет вид
.Тогда уравнение гиперболы (каноническое) имеет вид 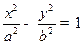 , где
, где 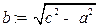 .
.
Определение Прямая 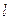 называется асимптотой неограниченной кривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю, когда точка неограниченно удаляется по кривой.
называется асимптотой неограниченной кривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю, когда точка неограниченно удаляется по кривой.
ЗАМЕЧАНИЕ 2 Прямые 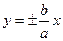 (Рис.2.13) являются асимптотами гиперболы при
(Рис.2.13) являются асимптотами гиперболы при 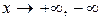 .
.
Определение Отрезки 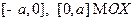 называются вещественными полуосями, а отрезки
называются вещественными полуосями, а отрезки 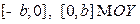 - мнимыми полуосями гиперболы. Точки
- мнимыми полуосями гиперболы. Точки 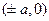 называются вершинами гиперболы.
называются вершинами гиперболы.
Определение Эксцентриситетом гиперболы называется величина 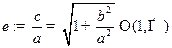 .
.
ЗАМЕЧАНИЕ 3 (геометрический смысл) Пусть 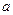 фиксировано.
фиксировано.
а) Тогда 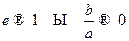 , то есть тогда и только тогда, когда асимптоты проворачиваются вокруг начала координат к оси
, то есть тогда и только тогда, когда асимптоты проворачиваются вокруг начала координат к оси 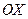 . При этом ветви гиперболы сжимаются к полуинтервалам
. При этом ветви гиперболы сжимаются к полуинтервалам 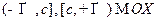 , а их фокусы приближаются к вершинам. б)
, а их фокусы приближаются к вершинам. б) 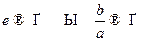 , то есть тогда и только тогда, когда асимптоты
, то есть тогда и только тогда, когда асимптоты
проворачиваются к оси 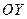 . При этом ветви гиперболы разгибаются в вертикальные прямые
. При этом ветви гиперболы разгибаются в вертикальные прямые 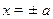 , а фокусы удаляются в бесконечность.
, а фокусы удаляются в бесконечность.
ЗАМЕЧАНИЕ 4 Уравнение касательной к гиперболе 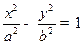 в точке
в точке 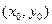
имеет вид 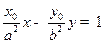 .
.
_____
Определение Парабола - множество точек в 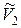 , расстояния от которых до заданной точки (фокуса) и до заданной прямой (директрисы) совпадают.
, расстояния от которых до заданной точки (фокуса) и до заданной прямой (директрисы) совпадают.
ЗАМЕЧАНИЕ 1 Пусть в какой-либо ПДСК уравнение директрисы 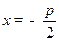 , а координаты фокуса
, а координаты фокуса 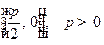 . Тогда уравнение параболы имеет вид
. Тогда уравнение параболы имеет вид 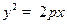 .
.
ЗАМЕЧАНИЕ 2 Точка параболы 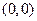 является ближайшей к директрисе и называется вершиной параболы.
является ближайшей к директрисе и называется вершиной параболы.
ЗАМЕЧАНИЕ 3 Уравнение касательной 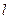 к параболе
к параболе 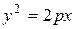 в точке
в точке 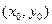 имеет вид
имеет вид 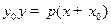 .
.
ТЕОРЕМА Уравнение кривой второго порядка с помощью последовательно: преобразования поворота ПДСК вокруг начала координат, последующего сдвига ПДСК на некоторый вектор и, возможно, отражения относительно какой-то из осей координат может быть приведено к одному из простейших видов:
1) каноническому уравнению эллипса, гиперболы, параболы; 2) уравнению пары прямых; 3) уравнению, которому удовлетворяют координаты одной точки;
4) уравнению, которому не удовлетворяют координаты ни одной точки.
_____
Определение Квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю, называется диагональной.
Определение Квадратная матрица называется квазидиагональной, если в ней можно выделить попарно непересекающиеся квадратные матрицы, главные диагонали которых заполняют главную диагональ исходной матрицы, а все элементы вне этих матриц равны нулю.
Определение Матрица 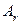 называется правой обратной к матрице
называется правой обратной к матрице  , если
, если 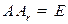 . Матрица
. Матрица 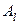 называется левой обратной к матрице
называется левой обратной к матрице  , если
, если 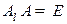 .
.
Определение Матрица  называется обратимой, если она имеет и правую и левую обратные матрицы.
называется обратимой, если она имеет и правую и левую обратные матрицы.
ТЕОРЕМА 1) Обратимая матрица необходимо является квадратной. При этом ее правая и левая обратные совпадают, и потому существует обратная матрица.
2) Если 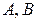 – квадратные матрицы одного размера, то
– квадратные матрицы одного размера, то 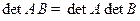 .
.
3) Квадратная матрица  имеет обратную тогда и только тогда, когда она не вырождена.
имеет обратную тогда и только тогда, когда она не вырождена.
4) 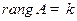 тогда и только тогда, когда
тогда и только тогда, когда  имеет равно
имеет равно 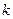 линейно независимых строк (столбцов), если последние рассматривать как векторы.
линейно независимых строк (столбцов), если последние рассматривать как векторы.
5) 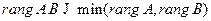 .
.
СЛЕДСТВИЕ 1 Если матрица  не вырождена, то для любой квадратной матрицы
не вырождена, то для любой квадратной матрицы 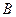 того же размера
того же размера 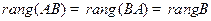 .
.
СЛЕДСТВИЕ 2 Произведение квадратных матриц не вырождено тогда и только тогда, когда не вырождены сомножители. Это следует из равенства 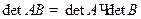 .
.
_____
Определение Характеристическим многочленом матрицы 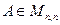 называется
называется
многочлен 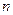 -ой степени
-ой степени 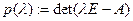 .
.
В поле комплексных чисел 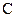 по теореме Гаусса он представим в виде
по теореме Гаусса он представим в виде 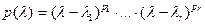 , где
, где 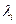 - попарно различные нули
- попарно различные нули 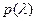 с соответствующими кратностями
с соответствующими кратностями 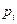 , и
, и 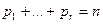
Определение Корни характеристического многочлена 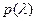 называются собственными числами матрицы
называются собственными числами матрицы  .
.
Определение Для собственного числа 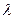 однородная СЛАУ
однородная СЛАУ 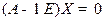 является совместной, но неопределенной в силу теоремы. Ее ненулевые решения называются собственными вектора ми матрицы
является совместной, но неопределенной в силу теоремы. Ее ненулевые решения называются собственными вектора ми матрицы  .
.
Определение Вещественная квадратная матрица  называется ортогональной, если она обратима и обратная матрица совпадает с сопряженной:
называется ортогональной, если она обратима и обратная матрица совпадает с сопряженной: 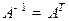 .
.
Определение Квадратная матрица  над называется симметричной, если
над называется симметричной, если 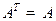 .
.
ТЕОРЕМА 1) (свойства ортогональных матриц)
а) Матрица 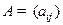 ортогональна тогда и только тогда, когда ее строки
ортогональна тогда и только тогда, когда ее строки
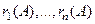 и столбцы
и столбцы 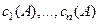 ортонормированны в
ортонормированны в 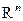 :
:
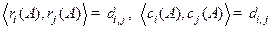 . При этом
. При этом 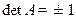 .
.
б) Ортогональная матрица размера 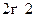 имеет один из двух видов:
имеет один из двух видов:
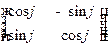 или
или 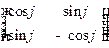 . В первом случае
. В первом случае 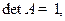
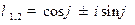 , а во втором случае
, а во втором случае 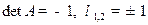 .
.
в) Ортогональная матрица размера 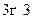 имеет вид
имеет вид 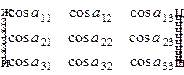 ,
,
и ее строки являются направляющими косинусами ортонормированной системы векторов 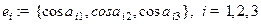 .
.
г) Собственные числа ортонормированной матрицы 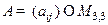 вычисляются по формулам
вычисляются по формулам 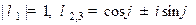 , где
, где 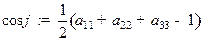 .
.
2) (свойства симметричных матриц)
а) Все собственные числа вещественной симметричной матрицы вещественны.
б) Для того, чтобы вещественная квадратная матрица  была симметричной, необходимо и достаточно, чтобы существовали ортогональная матрица
была симметричной, необходимо и достаточно, чтобы существовали ортогональная матрица 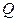 и диагональная матрица
и диагональная матрица 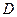 со свойством:
со свойством: 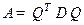 . При этом диагональные элементы матрицы
. При этом диагональные элементы матрицы 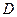 являются собственными числами матрицы
являются собственными числами матрицы  , а столбцы матрицы
, а столбцы матрицы 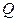 -
-
соответствующими собственными векторами матрица  .
.
3) (структура матриц общего вида) а) (QR-разложение) Каждая невырожденная
квадратная матрица представима в виде произведения ортогональной матрицы 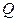 и верхнетреугольной матрицы
и верхнетреугольной матрицы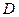 , диагональные элементы которой положительны.
, диагональные элементы которой положительны.
б) (полярное разложение) Каждая квадратная матрица  представима в виде произведения ортогональной матрицы
представима в виде произведения ортогональной матрицы 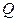 и симметричной матрицы
и симметричной матрицы 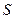 .
.
в) (сингулярное разложение) Каждая матрица 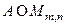 представима в виде
представима в виде 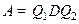 , где
, где 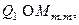
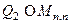 , есть ортогональные матрицы, а матрица
, есть ортогональные матрицы, а матрица 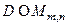 имеет в левом верхнем углу диагональную матрицу размера
имеет в левом верхнем углу диагональную матрицу размера 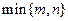 , а остальные ее элементы равны нулю.
, а остальные ее элементы равны нулю.
_____
Определение Поверхностью второго порядка в 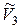 называется множество точек, координаты которых удовлетворяют уравнению вида
называется множество точек, координаты которых удовлетворяют уравнению вида
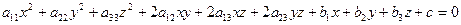 ,
,
или в матричной записи 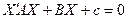 , где
, где 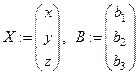 , а симметричная
, а симметричная
матрица 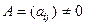 . Эллипсоидом называется множество точек в
. Эллипсоидом называется множество точек в 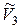 с ПДСК координаты которых удовлетворяют уравнению
с ПДСК координаты которых удовлетворяют уравнению 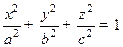 . Однополостным гиперболоидом называется множество точек, координаты которых удовлетворяют уравнению
. Однополостным гиперболоидом называется множество точек, координаты которых удовлетворяют уравнению 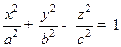 . Двуполостным гиперболоидом называется множествоточек, координаты которых удовлетворяют уравнению
. Двуполостным гиперболоидом называется множествоточек, координаты которых удовлетворяют уравнению 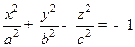 . Конической поверхностью (конусом) называется множество точек, координаты которых удовлетворяют уравнению
. Конической поверхностью (конусом) называется множество точек, координаты которых удовлетворяют уравнению 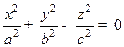 . Эллиптическим параболоидом называется множество точек, координаты которых удовлетворяют уравнению
. Эллиптическим параболоидом называется множество точек, координаты которых удовлетворяют уравнению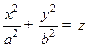 . Гиперболическим параболоидом (седлом) называется множество точек, координаты которых удовлетворяют уравнению
. Гиперболическим параболоидом (седлом) называется множество точек, координаты которых удовлетворяют уравнению 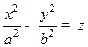 Эллиптическим цилиндром называется множество точек, координаты которых удовлетворяют уравнению
Эллиптическим цилиндром называется множество точек, координаты которых удовлетворяют уравнению 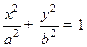 . Гиперболическим цилиндром называется множество точек, координаты которых удовлетворяют уравнению
. Гиперболическим цилиндром называется множество точек, координаты которых удовлетворяют уравнению 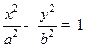 . Параболическим цилиндром называется множество точек, координаты которых удовлетворяют уравнению
. Параболическим цилиндром называется множество точек, координаты которых удовлетворяют уравнению 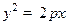 . Пара плоскостей
. Пара плоскостей 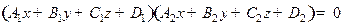 . Прямая или точка, например,
. Прямая или точка, например, 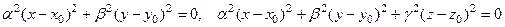 ,где
,где 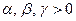 . Пустое множество, например,
. Пустое множество, например, 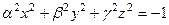 , где
, где 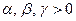 .
.
_____ Определение Движением 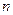 -мерного евклидова пространства
-мерного евклидова пространства 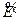 называется преобразование
называется преобразование 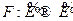 , сохраняющее расстояние между любыми двумя точками:
, сохраняющее расстояние между любыми двумя точками: 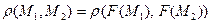 . ЗАМЕЧАНИЕ Движение в
. ЗАМЕЧАНИЕ Движение в 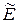 порождает преобразование на множестве векторов по правилу
порождает преобразование на множестве векторов по правилу 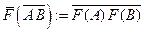 . Это преобразование сохраняет длины преобразованных векторов и углы между ними. Последнее следует из равенства треугольников
. Это преобразование сохраняет длины преобразованных векторов и углы между ними. Последнее следует из равенства треугольников 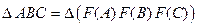 . Перечислим элементарные движения в
. Перечислим элементарные движения в 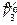 . 1) Вращение пространства
. 1) Вращение пространства 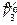 вокруг прямой. 2) Сдвиг всех точек пространства
вокруг прямой. 2) Сдвиг всех точек пространства 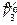 на один и тот же вектор. 3) Зеркальное отражение пространства
на один и тот же вектор. 3) Зеркальное отражение пространства 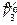 в какой-либо плоскости. ТЕОРЕМА 1) Пусть движение
в какой-либо плоскости. ТЕОРЕМА 1) Пусть движение 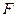 переводит ПДСК
переводит ПДСК 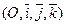 в ДПСК
в ДПСК 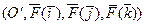 , где
, где 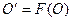 имеет координаты
имеет координаты 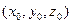 в исходной ПДСК и
в исходной ПДСК и 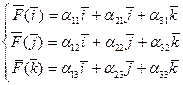 . (1)
. (1)
Тогда координаты в исходной ПДСК точки 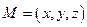 и ее образа
и ее образа 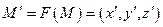 связаны равенствами
связаны равенствами 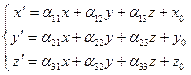 . (2) То есть движение
. (2) То есть движение 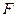 вполне определяется знанием преобразования одной ПДСК. Кроме того движение распадается на движение с неподвижной точкой
вполне определяется знанием преобразования одной ПДСК. Кроме того движение распадается на движение с неподвижной точкой 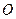 и ортогональной матрицей
и ортогональной матрицей 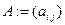
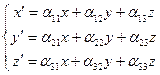 , (3) и на последующий сдвиг пространства
, (3) и на последующий сдвиг пространства 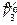 на вектор
на вектор 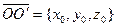 . 2) Движение (3) есть вращение пространства
. 2) Движение (3) есть вращение пространства 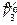 вокруг собственного вектора
вокруг собственного вектора 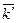 матрицы
матрицы  (
(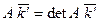 ) и последующего отражения (в случае
) и последующего отражения (в случае 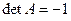 ) в плоскости, проходящей через точку
) в плоскости, проходящей через точку 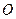 и перпендикулярной вектору
и перпендикулярной вектору 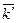 . 3) Пусть орты "старой"
. 3) Пусть орты "старой" 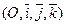 и "новой"
и "новой" 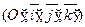 ПДСК в
ПДСК в 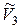 связаны равенством
связаны равенством 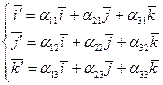 ;заданы новые координаты начала координат
;заданы новые координаты начала координат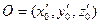 ;
; 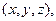
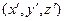 - координаты одной и той же точки в этих ПДСК. Тогда
- координаты одной и той же точки в этих ПДСК. Тогда 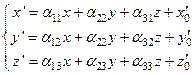 .
.
______ Определение Функция 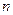 переменных
переменных 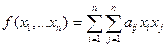 , где коэффициенты
, где коэффициенты 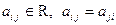 , а переменные,
, а переменные, 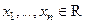 , называется квадратичной формой. ЗАМЕЧАНИЕ Образуем симметричную матрицу
, называется квадратичной формой. ЗАМЕЧАНИЕ Образуем симметричную матрицу 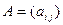 называемую матрицей квадратичной формы, и матрицу переменных
называемую матрицей квадратичной формы, и матрицу переменных 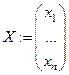 . Тогда квадратичная форма может быть записана в матричном виде
. Тогда квадратичная форма может быть записана в матричном виде 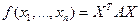 . Определение Квадратичные формы
. Определение Квадратичные формы 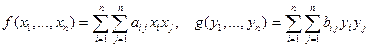 называются эквивалентными, если для некоторой невырожденной матрицы
называются эквивалентными, если для некоторой невырожденной матрицы 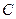
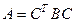 , то есть первая преобразуется во вторую после замены переменных
, то есть первая преобразуется во вторую после замены переменных 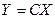 . ЗАМЕЧАНИЕ Каждая квадратичная форма
. ЗАМЕЧАНИЕ Каждая квадратичная форма 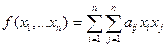 эквивалентна канонической квадратичной форме вида
эквивалентна канонической квадратичной форме вида 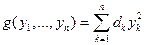 , причем соответствующую матрицу
, причем соответствующую матрицу 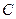 можно выбрать ортогональной. ТЕОРЕМА Уравнение поверхности второго порядка с помощью преобразования поворота пространства вокруг оси, проходящей через начало координат, последу ющего сдвига его на некоторый вектор, и, возможно, вращения вокруг координат ной оси и отражения в координатной плоскости, может быть приведено к уравне нию одного из 12 перечисленных выше типов геометрических объектов в
можно выбрать ортогональной. ТЕОРЕМА Уравнение поверхности второго порядка с помощью преобразования поворота пространства вокруг оси, проходящей через начало координат, последу ющего сдвига его на некоторый вектор, и, возможно, вращения вокруг координат ной оси и отражения в координатной плоскости, может быть приведено к уравне нию одного из 12 перечисленных выше типов геометрических объектов в 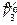 .
.
_____
Определение Суммой двух линейных операторов 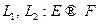 называется отображение, определяемое по правилу
называется отображение, определяемое по правилу 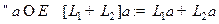 .
.
ЗАМЕЧАНИЕ Сумма двух линейных операторов является линейным оператором.
Определение Произведением числа 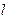 на линейный оператор
на линейный оператор 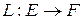 называется отображение, определяемое по правилу:
называется отображение, определяемое по правилу: 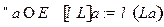 .
.
ЗАМЕЧАНИЕ Произведение числа на линейный оператор является линейным оператором.
Обозначение 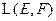 - множество всех линейных операторов из векторного пространства
- множество всех линейных операторов из векторного пространства 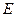 в векторное пространство
в векторное пространство 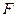 .
.
ЗАМЕЧАНИЕ Множество 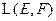 является векторным пространством
является векторным пространством
относительно введенных выше операций сложения и умножения на число. При этом нулевой оператор определяется по правилу: 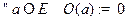 .
.
Определение Отображение 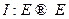 , определяемое по правилу:
, определяемое по правилу: 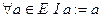 , называется тождественным преобразованием.
, называется тождественным преобразованием.
ЗАМЕЧАЕНИЕ 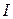 является линейным преобразованием.
является линейным преобразованием.
Определение Пусть 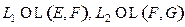 . Произведением (композицией) линейных операторов
. Произведением (композицией) линейных операторов 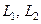 называется отображение
называется отображение 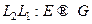 , определяемое по правилу:
, определяемое по правилу: 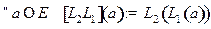 .
.
 2014-02-09
2014-02-09 675
675








