Оператором

ЗАМЕЧАНИЕ Произведение двух линейных операторов является линейным

Определение Пусть 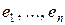- базис в 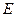, а 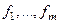- базис в 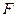. Пусть 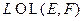и 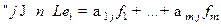. Тогда матрица коэффициентов 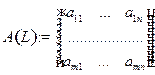называется матрицей оператора в базисах .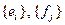

ТЕОРЕМА 1) Матрица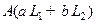линейной комбинации операторов совпадает с линейной комбинацией 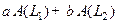матриц этих операторов.

2) Матрица произведения 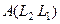двух линейных операторов совпадает с произведением матриц 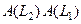этих операторов.

_____

Определение Множество 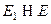называется подпространством векторного пространства 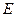, если .

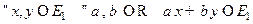ЗАМЕЧАНИЕ Подпространство удовлетворяет аксиомам 1)-8) и потому само является векторным пространством.

ЗАМЕЧАНИЕ 1) Линейная оболочка 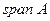является наименьшим векторным подпространством, содержащим .

2) Базисом в 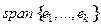является максимальная совокупность линейно независимых элементов среди .

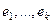Определение Ядром линейного оператора 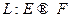называется множество

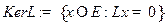Образом линейного оператора 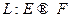называется множество .

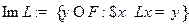ЗАМЕЧАНИЕ Ядро и образ оператора являются подпространствами

соответственно в .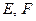

Определение Уравнение вида 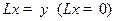, где 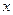- искомый, а 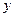- известный элемент, называется неоднородным (однородным) линейным операторным уравнением.

Определение Элемент 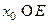называется решением такого уравнения, если при его подстановке вместо 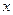, уравнение обращается в равенство.

Определение Решить уравнение это значит, найти все его решения.

Следующее понятие используется при исследовании разрешимости операторных уравнений.

Определение Рангом линейного оператора называется размерность образа 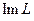этого оператора.

ТЕОРЕМА Пусть .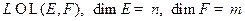

1) Разрешимость операторного уравнения 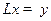при выделенных базисах 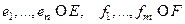равносильна разрешимости СЛАУ 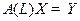, где

.

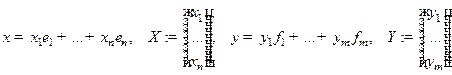2) Ранг линейного оператора совпадает с рангом матрицы этого оператора.

3) 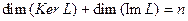. 4) Если 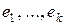- базис в ядре 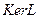, то произвольное (общее) решение однородного операторного уравнения 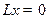имеет вид:

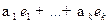, где .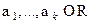

5) Если 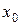- какое-либо частное решение неоднородного операторного уравнения 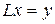, то произвольное (общее) решение этого уравнения имеет вид .

_____

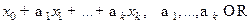Определение Линейные операторы 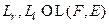называется соответственно правым и левым обратным к линейному оператору 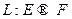, если

.

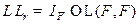
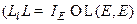Определение Линейный оператор 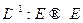называется обратимым, если существуют и правый и левый обратные к нему.

ЗАМЕЧАНИЕ Для обратимого оператора как и в случае матриц доказывается, что 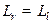. Поэтому можно говорить об обратном к операторе .

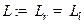Определение Линейный оператор 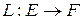называется взаимно однозначным (мономорфизмом), если он преобразует разные элементы в разные: .

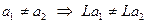ЗАМЕЧАНИЕ 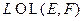является мономорфизмом тогда и только тогда, когда

однородное уравнение 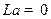имеет единственное (то есть нулевое) решение.

Определение Линейное отображение 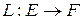называется отображением "на" (эпиморфизмом), если 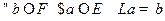, то есть операторное уравнение 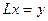имеет решение в 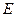для каждой правой части .

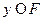ЗАМЕЧАНИЕ Линейное отображение 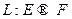является изоморфизмом (в соответствии с определением) тогда и только тогда, когда оно является мономорфизмом и эпиморфизмом.