Определение Пусть функция 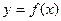 определена на
определена на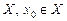 и является предельной точкой. Если существует конечный предел
и является предельной точкой. Если существует конечный предел 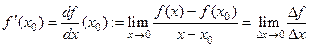
то он называется производной функцией  в точке
в точке 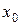 .
.
ЗАМЕЧАНИЕ Если функция 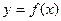 имеет производную в точке
имеет производную в точке 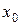 , то она непрерывна в этой точке. Обратное, вообще говоря, неверно.
, то она непрерывна в этой точке. Обратное, вообще говоря, неверно.
_____
Определение Если существует конечный предел 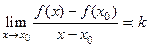 , то говорят, что график функции
, то говорят, что график функции  имеет касательную в точке
имеет касательную в точке 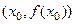 . Уравнение
. Уравнение 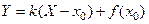 называется уравнением касательной, а число
называется уравнением касательной, а число 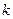 - угловым коэффициентом касательной.
- угловым коэффициентом касательной.
ЗАМЕЧАНИЕ Касательная в смысле данного определения удовлетворяет соотношению 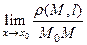 из общего определения касательной.
из общего определения касательной.
СЛЕДСТВИЕ (геометрический смысл производной) График функции  имеет касательную в точке
имеет касательную в точке 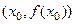 тогда и только тогда, когда
тогда и только тогда, когда  имеет производную в
имеет производную в 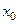 . В этом случае угловой коэффициент касательной
. В этом случае угловой коэффициент касательной 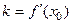 .
.
Определение Если график функции имеет касательную в точке 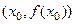 , то прямая
, то прямая 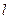 проходящая через эту точку и перпендикулярная к касательной, называется нормалью к графику в
проходящая через эту точку и перпендикулярная к касательной, называется нормалью к графику в 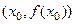 .
.
ЗАМЕЧАНИЕ Так как вектор нормали к касательной 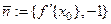 перпендикулярен вектору
перпендикулярен вектору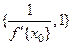 , то уравнение нормали можно записать в виде
, то уравнение нормали можно записать в виде
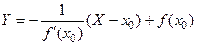
____
Определение Правой (левой) производной функции 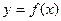 в точке
в точке 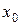 называется конечный предел
называется конечный предел 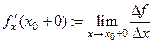
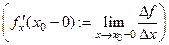 , если он существует.
, если он существует.
ТЕОРЕМА (правила дифференцирования) 1) 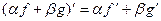 .
.
2) 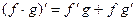 3)
3) 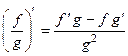 в тех точках, где знаменатель не равен нулю. 4) Пусть
в тех точках, где знаменатель не равен нулю. 4) Пусть 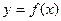 монотонна, непрерывна в окрестности
монотонна, непрерывна в окрестности 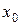 и дифференци- руема в
и дифференци- руема в 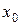 и
и 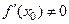 ,
, 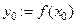 . Тогда обратная функция
. Тогда обратная функция 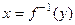 монотонна, непрерывна в окрестности точки
монотонна, непрерывна в окрестности точки 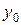 , дифференцируема в
, дифференцируема в 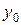 и
и 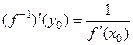 . 5) (производная сложной функции) Пусть функция
. 5) (производная сложной функции) Пусть функция 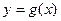 определена в окрестности
определена в окрестности 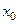 и дифференцируема в
и дифференцируема в 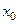 ; пусть
; пусть 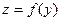 определена в окрестности
определена в окрестности 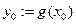 и дифференцируема в
и дифференцируема в 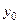 . Тогда функция
. Тогда функция 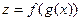
дифференцируема в окрестности 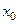 и
и 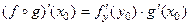 .
.
_____
Определение Пусть функция 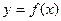 определена в окрестности точки
определена в окрестности точки 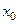 . Говорят, что
. Говорят, что  - дифференцируема (расчленима) в точке
- дифференцируема (расчленима) в точке 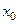 если
если 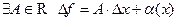 , где
, где 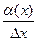 есть БМ при
есть БМ при 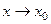 . Если
. Если  дифференцируема в
дифференцируема в 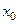 , то слагаемое
, то слагаемое 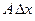 называется дифференциалом функции
называется дифференциалом функции  . Обозначение
. Обозначение 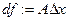 .
.
ТЕОРЕМА (свойства дифференциала). 1) Функция  дифференцируема в
дифференцируема в 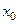 тогда и только тогда, когда она имеет производную в
тогда и только тогда, когда она имеет производную в 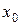 . При этом
. При этом 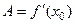 .
.
2) 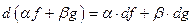 . 3)
. 3) 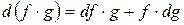 . 4)
. 4) 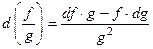 .
.
5) (инвариантность дифференциала при замене) Если функция 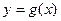 дифференцируема в точке
дифференцируема в точке 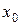 , а
, а 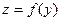 дифференцируема в точке
дифференцируема в точке 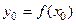 , то сложная функция
, то сложная функция 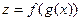 дифференцируема в
дифференцируема в 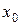 и
и 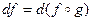 .
.
ЗАМЕЧАНИЕ 1 Ввиду первого утверждения теоремы термины "дифференцируемая функция" и "функция, имеющая производную" взаимозаменяемы.
ЗАМЕЧАНИЕ 2 (геометрический смысл дифференциала) Так как уравнение
касателной к графику функции 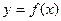 в точке
в точке 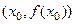 имеет вид
имеет вид 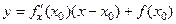 , то дифференциал
, то дифференциал 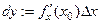 в точке
в точке 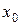 совпадает, очевидно, с приращением
совпадает, очевидно, с приращением 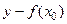 ординаты касательной, проведенной в этой точке.
ординаты касательной, проведенной в этой точке.
ЗАМЕЧАНИЕ 3 При условии 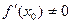 имеет место приближенное равенство
имеет место приближенное равенство 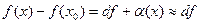 , которое используется для приближенного вычисления значений функции.
, которое используется для приближенного вычисления значений функции.
_____
Определение Производной нулевого порядка функции в точке называется ее значение в этой точке. Пусть существует производная 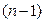 - го порядка
- го порядка 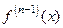 в каждой точке некоторой окрестности точки
в каждой точке некоторой окрестности точки 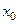 . Если существует конечный предел
. Если существует конечный предел
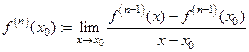 ,
,
то он называется производной n-го порядка функции  в точке
в точке 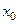 .
.
Обозначение 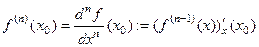 . Исторически приняты обозначения
. Исторически приняты обозначения 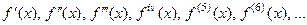 .
.
Определение (физический смысл производной). Пусть материальная точка движется вдоль оси 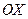 по закону
по закону 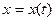 . Средней скоростью движения на промежутке
. Средней скоростью движения на промежутке 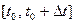
 называется величина
называется величина 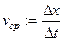 . Мгновенной скоростью движения в момент времени
. Мгновенной скоростью движения в момент времени 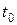 называется
называется
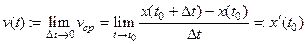 .
.
Средним ускорением на промежутке 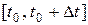 называется величина
называется величина 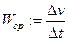 . Мгновенным ускорением в момент времени
. Мгновенным ускорением в момент времени 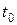 называется
называется
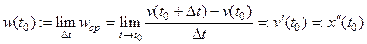 .
.
_____
Определение Функция 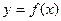 называется дифференцируемой на множестве
называется дифференцируемой на множестве , если она имеет производную в каждой точке
, если она имеет производную в каждой точке 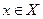 .
.
ТЕОРЕМА Пусть функции 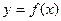 ,
, 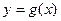 непрерывны на
непрерывны на 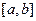 , дифференцируемы на
, дифференцируемы на 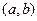 и
и 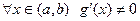 . Тогда: 1) (теорема Ролля) если
. Тогда: 1) (теорема Ролля) если 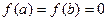 , то
, то 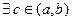
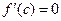 . 2) (теорема Коши)
. 2) (теорема Коши) 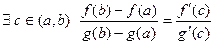 . 3) (правило Лопиталя) Если
. 3) (правило Лопиталя) Если 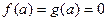 и существует конечный предел
и существует конечный предел 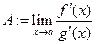 , то существует
, то существует 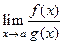 и он равен
и он равен  .
.
СЛЕДСТВИЕ (формула Лагранжа) Теорема Коши при 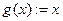 принимает вид
принимает вид 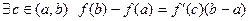 .
.
ЗАМЕЧАНИЕ Если функции 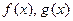 дифференцируемы на
дифференцируемы на 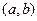 и
и 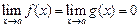 или
или 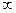 , то из
, то из 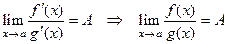 .
.
_____
Определение Точка 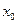 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции  , если
, если 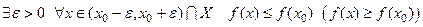 . Точки
. Точки
локальных максимумов и минимумов называются точками локального экстремума.
ТЕОРЕМА (о локальном экстремуме) 1) Если  не возрастает (не убывает) и дифференцируема на
не возрастает (не убывает) и дифференцируема на 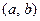 , то
, то 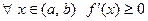 .
.
2) Если 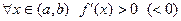 , то
, то  возрастает (убывает) на
возрастает (убывает) на 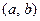 .
.
3) (теорема Ферма) Если 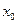 - точка локального экстремума функции
- точка локального экстремума функции  , и
, и  дифференцируема в
дифференцируема в 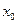 , то
, то 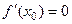 .
.
4) (первое достаточное условие экстремума). Пусть  дифференцируема на
дифференцируема на 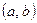 ,
, 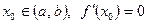 . Если
. Если 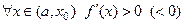 и
и 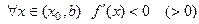 , то
, то 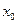 - точка максимума (минимума) на
- точка максимума (минимума) на 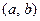 .
.
5) (второе достаточное условие локального экстремума). Пусть  имеет вторую производную
имеет вторую производную 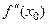 и
и 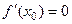 . Если
. Если 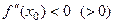 , то
, то 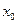 - точка локального максимума (минимума).
- точка локального максимума (минимума).
Определение Пусть функция 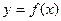 определена на
определена на 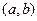 , и ее график имеет
, и ее график имеет
касательную в каждой точке 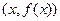 . Говорят, что эта кривая выпукла (вогнута) на
. Говорят, что эта кривая выпукла (вогнута) на 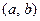 , если она лежит выше (ниже) любой своей касательной.
, если она лежит выше (ниже) любой своей касательной.
Определение Точка 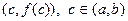 , называется точкой перегиба кривой, если эта кривая выпукла (вогнута) на
, называется точкой перегиба кривой, если эта кривая выпукла (вогнута) на 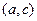 и вогнута (выпукла) на
и вогнута (выпукла) на 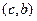 .
.
ТЕОРЕМА Пусть  дважды дифференцируема на
дважды дифференцируема на 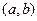 . 1) (необходимые условия выпуклости) Если кривая выпукла (вогнута) на
. 1) (необходимые условия выпуклости) Если кривая выпукла (вогнута) на 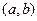 , то
, то 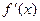 не убывает (не возрастает) на
не убывает (не возрастает) на 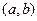 и
и 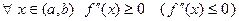 . 2) (достаточные условия выпуклости) Если
. 2) (достаточные условия выпуклости) Если 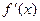 монотонно возрастает (убывает) на
монотонно возрастает (убывает) на 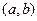 или
или 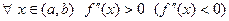 , то кривая выпукла (вогнута) на
, то кривая выпукла (вогнута) на 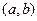 . 3) (необходимые условия точки перегиба). Если
. 3) (необходимые условия точки перегиба). Если 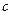 - точка перегиба кривой, то
- точка перегиба кривой, то 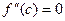 .
.
Важной характеристикой гладкой кривой и одновременно мерой ее выпуклости является понятие кривизны.
Определение Пусть дана гладкая кривая 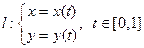 , то есть функции
, то есть функции 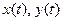 непрерывно дифференцируемы на
непрерывно дифференцируемы на 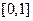 и все ее точки неособые. Обозначим
и все ее точки неособые. Обозначим 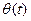 угол наклона касательной в точке
угол наклона касательной в точке 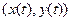 кривой, а
кривой, а 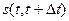 - длину дуги между точками
- длину дуги между точками 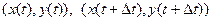 этой кривой. Предел
этой кривой. Предел 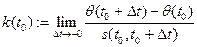 отношения приращения угла наклона касательной к длине соответствующей дуги, если он существует, называется кривизной кривой в точке
отношения приращения угла наклона касательной к длине соответствующей дуги, если он существует, называется кривизной кривой в точке 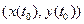 .
.
ЗАМЕЧАНИЕ Если функции 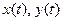 дважды дифференцируемы, то кривизна кривой в точке
дважды дифференцируемы, то кривизна кривой в точке 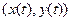 вычисляется по формуле
вычисляется по формуле 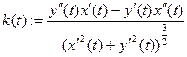 .
.
СЛЕДСТВИЕ Если кривая задана уравнением 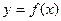 , то
, то 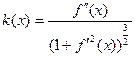 .
.
Из этой формулы и предыдущей теоремы следует, что положительное значение кривизны означает выпуклость, а отрицательное значение - вогнутость кривой в соответствующей точке. Кривыми с нулевой кривизной 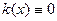 являются прямые и только они.
являются прямые и только они.
_____
Определение Пусть функция 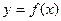 определена на некотором интервале
определена на некотором интервале 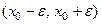 и имеет на нем производные до
и имеет на нем производные до 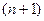 -го порядка включительно. Многочлен степени
-го порядка включительно. Многочлен степени 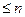
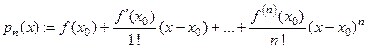 называется многочленом Тейлора. Разность
называется многочленом Тейлора. Разность 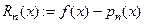 - остаточным членом. Формула
- остаточным членом. Формула 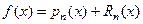 - формула Тейлора.
- формула Тейлора.
ТЕОРЕМА (свойства формулы Тейлора) 1) Многочлен Тейлора является единственным многочленом степени 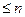 , который удовлетворяет равенствам:
, который удовлетворяет равенствам:
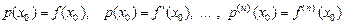 .
.
2) Остаточный член 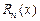 можно представить в форме Лагранжа
можно представить в форме Лагранжа
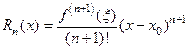 , где число
, где число 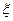 находится между
находится между 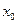 и
и 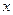 .
.
ЗАМЕЧАНИЕ 1 В теореме остаточный член можно записать менее точно, в форме Пеано 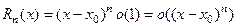 .
.
ЗАМЕЧАНИЕ 2 При 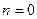 формула Тейлора с остаточным членом в форме Лагранжа
формула Тейлора с остаточным членом в форме Лагранжа 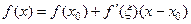 совпадает с формулой Лагранжа. При
совпадает с формулой Лагранжа. При 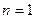 формула Тейлора с остаточнымчленом в форме Пеано совпадает с формулой дифференциала.
формула Тейлора с остаточнымчленом в форме Пеано совпадает с формулой дифференциала.
ЗАМЕЧАНИЕ Для 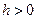 положим
положим 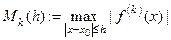 . Тогда
. Тогда
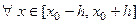
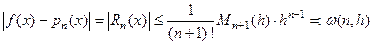 .
.
Формула Тейлора позволяет решать следующие три задачи.
1) По заданным степени 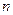 многочлена и длине отрезка
многочлена и длине отрезка 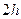 оценить в терминах
оценить в терминах 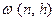 величину отклонения
величину отклонения 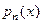 от
от  на
на 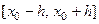
2) При заданным длине отрезка 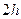 и точности
и точности 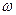 определить степень
определить степень 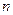 многочлена
многочлена 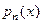 , отклонение которого от
, отклонение которого от  на
на 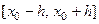 не превышает
не превышает 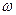 .
.
3) По заданным степени многочлена 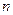 и точности
и точности 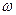 определить максимальную длину
определить максимальную длину 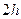 отрезка
отрезка 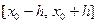 , на котором
, на котором 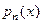 отклоняется от
отклоняется от  не более, чем на
не более, чем на 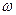 .
.
_____
В заключение параграфа рассмотрим два случая расположения асимптот неограниченной кривой.
1) Асимптота 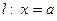 вертикальная. В этом случае расстояние от переменной точки
вертикальная. В этом случае расстояние от переменной точки 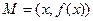 кривой до асимптоты
кривой до асимптоты 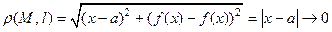 ,
,
когда 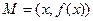 стремится к бесконечности. Отсюда необходимо
стремится к бесконечности. Отсюда необходимо 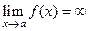 .
.
2) Асимптота 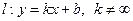 наклонная. По определению асимптоты
наклонная. По определению асимптоты 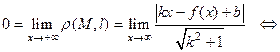

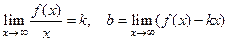 .
.
_____
Определение Пусть функции 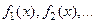 определены на непустом множестве
определены на непустом множестве  , являющемся общей частью их областей определения. Выражение вида
, являющемся общей частью их областей определения. Выражение вида 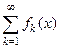 называется функциональным рядом. Множество точек
называется функциональным рядом. Множество точек 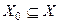 , в каждой из которых соответствующий числовой ряд
, в каждой из которых соответствующий числовой ряд 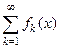 сходится, называется множеством сходимости функционального ряда.
сходится, называется множеством сходимости функционального ряда.
ЗАМЕЧАНИЕ Если существует 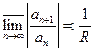 или
или 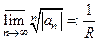 , то в силу признаков
, то в силу признаков
соответственно Даламбера и Коши степенной ряд абсолютно сходится во всех
точках интервала 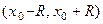 и расходится во всех точках вне отрезка
и расходится во всех точках вне отрезка 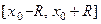 .
. 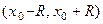 называется интервалом сходимости, а число
называется интервалом сходимости, а число 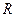 - радиусом сходимости степенного ряда
- радиусом сходимости степенного ряда 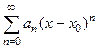 .
.
Определение Функция 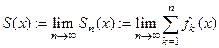 , определенная на множестве
, определенная на множестве
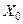 , называется суммой функционального ряда. При этом для степенного ряда
, называется суммой функционального ряда. При этом для степенного ряда
удобно обозначать 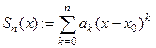 .
.
Определение Функциональный ряд 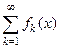 называется равномерно сходящимся на множестве
называется равномерно сходящимся на множестве 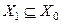 к своей сумме
к своей сумме 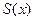 , если
, если 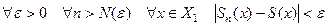 .
.
Понятие равномерной сходимости позволяет перенести свойство непрерывности членов ряда на его сумму.
ЗАМЕЧАНИЕ Если функции 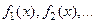 непрерывны на множестве равномер- ной сходимости
непрерывны на множестве равномер- ной сходимости 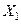 , то и сумма
, то и сумма 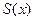 ряда
ряда 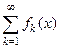 непрерывна на этом множестве.
непрерывна на этом множестве.
Определение Если функция  имеет производные любого порядка в точке
имеет производные любого порядка в точке 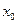 , то степенной ряд вида
, то степенной ряд вида 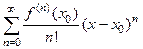 называется рядом Тейлора функции
называется рядом Тейлора функции  . В случае
. В случае 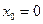 ряд
ряд 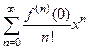 называется рядом Маклорена функции
называется рядом Маклорена функции  .
.
Определение Пусть функция  имеет производные любого порядка в точке
имеет производные любого порядка в точке 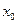 и пусть
и пусть 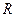 - радиус сходимости ее ряда Тейлора. Если на
- радиус сходимости ее ряда Тейлора. Если на 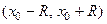
 совпадает с суммой
совпадает с суммой 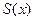 этого ряда, то
этого ряда, то  называется аналитической функцией на
называется аналитической функцией на 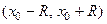
ТЕОРЕМА (свойства функциональных рядов) 1) Если 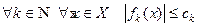 и числовой ряд
и числовой ряд 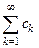 сходится, то ряд
сходится, то ряд 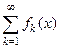 равномерно сходится на
равномерно сходится на  .
.
2) Пусть функции 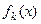 непрерывны отрезке
непрерывны отрезке 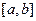 и ряд
и ряд 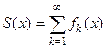 равномерно сходится на
равномерно сходится на 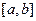 . Тогда его можно почленно интегрировать: числовой ряд
. Тогда его можно почленно интегрировать: числовой ряд 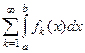 сходится к
сходится к 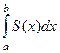 . 3) Пусть функции
. 3) Пусть функции 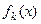 имеют непрерывную производную на отрезке
имеют непрерывную производную на отрезке 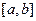 . Пусть ряд
. Пусть ряд 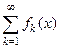 сходится в некоторой точке
сходится в некоторой точке 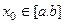 , а ряд из производных
, а ряд из производных 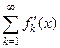 равномерно сходится на
равномерно сходится на 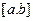 . Тогда функциональный ряд
. Тогда функциональный ряд 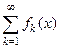 равномерно сходится на
равномерно сходится на 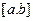 к дифференцируемой функции
к дифференцируемой функции 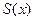 и
и 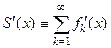 .
.
4) Сумма 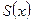 степенного ряда
степенного ряда 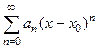 имеет производные любого порядка в каждой точке интервала сходимости, причем
имеет производные любого порядка в каждой точке интервала сходимости, причем
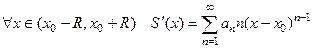 .
.
5) Если функция  представима в окрестности точки
представима в окрестности точки 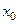 в виде суммы степенного ряда
в виде суммы степенного ряда 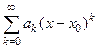 , то необходимо
, то необходимо 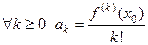 , то есть она необходимо продолжается до аналитической функции на интервале сходимости ряда.
, то есть она необходимо продолжается до аналитической функции на интервале сходимости ряда.
6) Функция 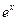 аналитическая на
аналитическая на 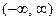 и
и 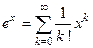 ;
;
функция 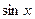 аналитическая на
аналитическая на 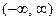 и
и 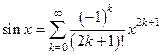 ;
;
функция 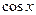 аналитическая на
аналитическая на 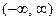 и
и 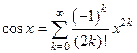 ;
;
функция 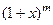 аналитическая на
аналитическая на 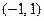 и
и 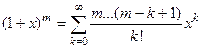 ;
;
функция 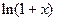 аналитическая на
аналитическая на 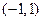 и
и 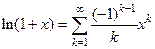 .
.
 2014-02-09
2014-02-09 880
880








