Под множеством будем понимать совокупность элементов, обладающим каким-либо свойством.
Обозначение Множество обозначается прописными латинскими буквами 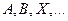 ; элементы – строчными латинскими
; элементы – строчными латинскими 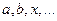 ; свойство представляет собой предложение или формулу
; свойство представляет собой предложение или формулу 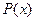 , содержащие обозначение элемента. Запись
, содержащие обозначение элемента. Запись 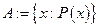 читается "
читается " по определению есть множество элементов
по определению есть множество элементов 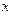 , которые обладают свойством
, которые обладают свойством 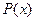
ПРИМЕР Множество 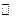 натуральных чисел
натуральных чисел 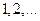 . Множество
. Множество 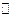 целых чисел
целых чисел 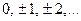 . Множество
. Множество 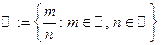 рациональных чисел (дробей). Множество действительных (вещественных) чисел
рациональных чисел (дробей). Множество действительных (вещественных) чисел 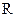 , которое состоит из множества рациональных чисел
, которое состоит из множества рациональных чисел 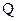 и множества иррациональных чисел
и множества иррациональных чисел 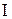 . Иррациональными являются, например, числа
. Иррациональными являются, например, числа 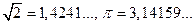 ,
, 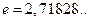 ..
..
ЗАМЕЧАНИЕ Действительной число рационально тогда и только тогда, когда оно представимо периодической десятичной дробью.
Определение Множество, не содержащее элементов, называется пустым.
Обозначение 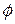 .
.
Определение Множество 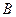 , все элементы которого принадлежат
, все элементы которого принадлежат  , называется подмножеством множества
, называется подмножеством множества  .
.
Обозначение 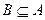 . Если же
. Если же 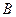 является подмножеством, но не совпадает с
является подмножеством, но не совпадает с  , то
, то 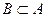 .
.
Определение Множества 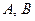 совпадают, если
совпадают, если 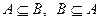 . Обозначение
. Обозначение 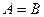 .
.
Определение Декартовым произведением множеств 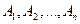 называется множество упорядоченных
называется множество упорядоченных 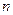 -ок элементов
-ок элементов
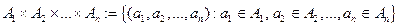 .
.
ЗАМЕЧАНИЕ Если 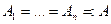 , то
, то 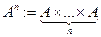 .
.
_____
Определение Высказывание – предложение, о котором можно сказать, что оно истинно или ложно.
Обозначение Если нас интересует высказывание безотносительно к его истинности или ложности, то оно обозначается большими латинскими буквами 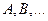 . Истинное высказывание обозначается
. Истинное высказывание обозначается 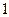 , а ложное -
, а ложное - 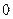 .
.
Определим 5 операций над высказываниями.
Определение Отрицанием высказывания  называется высказывание, которое истинно, если
называется высказывание, которое истинно, если  ложно, и наоборот, ложно, если
ложно, и наоборот, ложно, если  истинно.
истинно.
Обозначение 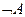 или
или 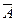 . Читается "неверно, что
. Читается "неверно, что  ".
".
Истинностная таблица операции отрицания есть 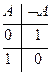
Определение Дизъюнкцией высказываний 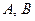 называется высказывание, которое истинно, когда истинно или
называется высказывание, которое истинно, когда истинно или  или
или 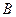 , или оба вместе.
, или оба вместе.
Обозначение 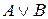 . Читается "
. Читается " или
или 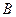 ".
".
Истинностная таблица операции дизъюнкции 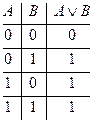
Определение Конъюнкцией высказываний 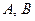 называется
называется
высказывание, которое истинно тогда и только тогда, когда и 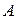 и
и 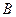
истинны. Обозначение 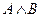 или просто
или просто 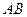 .Читается "
.Читается " и
и 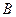 ".
".
Истинностная таблица конъюнкции 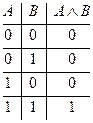
Определение Импликацией высказываний 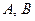 называется высказывание, которое ложно тогда и только тогда, когда
называется высказывание, которое ложно тогда и только тогда, когда 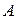 истинно, а
истинно, а 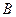 ложно.
ложно.
Обозначение 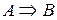 . Читается "если
. Читается "если  , то
, то 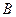 " или "из
" или "из  следует
следует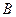 .
.
Истинностная таблица импликации 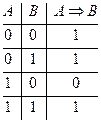
Определение Эквиваленцией высказываний 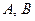 называется высказывание, которое истинно тогда и только тогда, когда
называется высказывание, которое истинно тогда и только тогда, когда 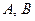 оба истинны или оба ложны. Обозначение
оба истинны или оба ложны. Обозначение 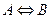 . Читается "
. Читается " тогда и только тогда, когда
тогда и только тогда, когда 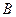 ", или "
", или " равносильно
равносильно 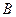 ".
".
Истинностная таблица операции эквиваленции 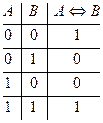
_____
Определение Высказывание, получаемое из какой-либо группы исходных (элементарных, простых) с помощью 5 операций, называется формулой (логической).
Порядок выполнения операций в формуле следующий: 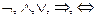 .
.
Порядок можно изменить расстановкой скобок.
Определение Переменные, принимающие только два значения 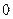 или
или 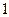 , называются двоичными. Функция от
, называются двоичными. Функция от 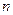 двоичных переменных, принимающая только два значения
двоичных переменных, принимающая только два значения 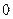 или
или 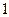 , называется булевой функцией.
, называется булевой функцией.
Каждая формула порождает булеву функцию, которая задается истинностной
таблицей.
Определение Формулы называются эквивалентным (равносильными), если их булевы функции совпадают. Обозначение 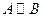 .
.
Определение Теорема, формулируемая в форме высказывания 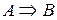 называется прямой. Образованное из нее высказывание
называется прямой. Образованное из нее высказывание 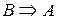 - обратной теоремой. Высказывание вида
- обратной теоремой. Высказывание вида 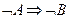 называется противоположной теоремой, а высказывание
называется противоположной теоремой, а высказывание 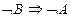 - теоремой, обратной к противоположной.
- теоремой, обратной к противоположной.
ЗАМЕЧАНИЕ Прямая теорема равносильна обратной к противоположной; обратная теорема равносильна противоположной.
Это следует из совпадения соответствующих таблиц истинности.
Определение Методом доказательства от противного теоремы 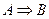 называется доказательство равносильной ей теоремы
называется доказательство равносильной ей теоремы 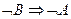 .
.
Определение Теорема, формулируемая в форме 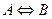 , называется критерием.
, называется критерием.
ЗАМЕЧАНИЕ Так как 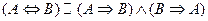 , то доказательство критерия равносильно доказательству двух теорем - прямой и обратной.
, то доказательство критерия равносильно доказательству двух теорем - прямой и обратной.
_____
Определение Понятия, обладающие объемом с числом объектов 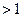 называются предметными переменными, а их объем называется областью определения предметной переменной. Конкретные значения (реализации, интерпретации, примеры) этих понятий, а также имена собственные называются предметными постоянными. Предметные постоянные и предметные переменные называются термами.
называются предметными переменными, а их объем называется областью определения предметной переменной. Конкретные значения (реализации, интерпретации, примеры) этих понятий, а также имена собственные называются предметными постоянными. Предметные постоянные и предметные переменные называются термами.
Определение Предложение, содержащее термы, называется высказывательной функцией (предикатом), если оно становится высказыванием всякий раз, когда входящие в него предметные переменные принимают конкретные значения.
Определение Предикат называется n-местным, если он содержит 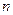 предметных переменных. Обозначение
предметных переменных. Обозначение 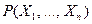 .
.
ЗАМЕЧАНИЕ 0-местный предикат естественно считать высказыванием.
Определение Областью определения предиката называется множеств 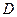
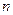 -ок значений
-ок значений 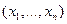 , которые могут принимать предметные переменные
, которые могут принимать предметные переменные 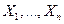 .
.
Для предиката 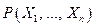 обозначим
обозначим 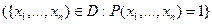 подмножество тех
подмножество тех 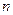 -ок переменных, на которых этот предикат превращается в истинное высказывание.
-ок переменных, на которых этот предикат превращается в истинное высказывание.
Определение Квантором общности называется операция перехода от 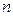 - местного предиката
- местного предиката 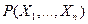 к
к 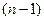 -местному предикату, которая читается так: "для каждого
-местному предикату, которая читается так: "для каждого 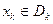 имеет место
имеет место 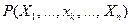 ".
".
Обозначение 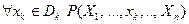 .
.
Определение Переменная 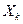 предиката
предиката 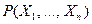 называется свободной, а
называется свободной, а
исчезнувшая переменная 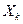 предиката
предиката 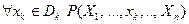 называется
называется
связанной.
Определение Квантором существования называется операция перехода от 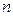 -местного предиката
-местного предиката 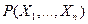 к
к 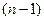 -местному, которая читается так: "для некоторого
-местному, которая читается так: "для некоторого 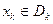 имеет место
имеет место 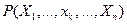 ".
".
Обозначение 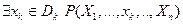 .
.
ЗАМЕЧАНИЕ Над предикатами можно производить пять логических операций.
 2014-02-09
2014-02-09 1642
1642








