Определение Объединением множеств 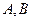 называется
называется 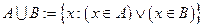 .
.
Определение Пересечением множеств 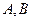 называется
называется  .
.
Определение Множества 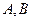 называются непересекающимися, если
называются непересекающимися, если 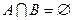 .
.
Определение Разбиением множества  называется совокупность
называется совокупность 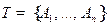 попарно непересекающихся его подмножеств со свойством
попарно непересекающихся его подмножеств со свойством 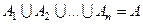 .
.
Определение Разностью множеств 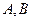 называется
называется 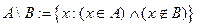 .
.
Определение Пусть дано отображение 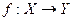 множества
множества  в множество
в множество 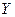 . В обозначении
. В обозначении 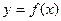
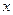 называется независимой переменной величиной с областью определения
называется независимой переменной величиной с областью определения  ;
; 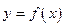 - зависимой переменной величиной с множеством значений
- зависимой переменной величиной с множеством значений
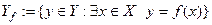 ;
; 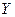 называется областью значений отображения.
называется областью значений отображения.
Определение Графиком отображения 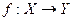 называется подмножество декартова произведения
называется подмножество декартова произведения 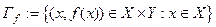 .
.
Определение Отображение 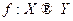 называется инъективным (взаимно однознач ным), если она разным элементам из
называется инъективным (взаимно однознач ным), если она разным элементам из  сопоставляет разные элементы из
сопоставляет разные элементы из 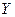 .
.
Определение Отображение 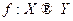 называется сюръективным (отображением "на"), если
называется сюръективным (отображением "на"), если 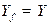 .
.
Определение Отображение 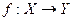 называется биективным (биекцией), если она инъективно и сюръективно.
называется биективным (биекцией), если она инъективно и сюръективно.
ЗАМЕЧАНИЕ Биективное отображение и только такое отображение имеет обратное 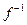 . При этом область определения последнего есть
. При этом область определения последнего есть 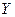 .
.
_____
Определение Множества 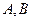 называются равномощными, если существует биекция
называются равномощными, если существует биекция  на
на 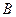 .
.
Определение Мощностью конечного множества называется число его элементов.
Обозначение 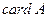
Определение Множество называется счетным, если оно равномощно множеству 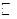 .
.
Определение Множество называется множеством мощности континуум, если оно равномощно множеству 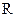 .
.
Определение Множество элементов называется упорядоченным, если для любых его двух элементов всегда можно сказать, что один из них предшествует другому.
ЗАМЕЧАНИЕ Если на вещественной оси выбрать начало координат и масштаб, то между множествами 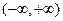 и
и 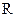 можно установить взаимно однозначное соответствие (то есть они равномощны), при котором сохраняется отношение порядка. Поэтому в дальнейшем мы иногда не будем различать эти два
можно установить взаимно однозначное соответствие (то есть они равномощны), при котором сохраняется отношение порядка. Поэтому в дальнейшем мы иногда не будем различать эти два
упорядоченных множества (точек и чисел).
Определение Множество точек 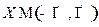 называется ограниченым сверху
называется ограниченым сверху
(снизу) если 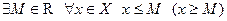 ; множество ограничено, если оно
; множество ограничено, если оно
ограниченно и сверху и снизу: 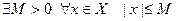 .
.
Определение Точной верхней (нижней) гранью множества 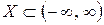 называется наименьшее (наибольшее) число
называется наименьшее (наибольшее) число 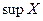
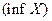 со свойствами
со свойствами 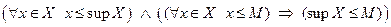
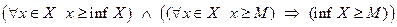 .
.
_____
Определение Композицией отображений 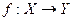 и
и 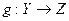 называется отображение
называется отображение 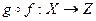 , определяемое по правилу
, определяемое по правилу 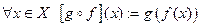 .
.
Определение Преобразование 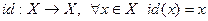 , называется тождественным отображением.
, называется тождественным отображением.
Определение Отображение 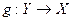 называется правым (левым) обратным к отображению
называется правым (левым) обратным к отображению 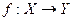 , если
, если 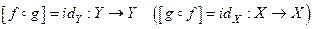 .
.
Отображение 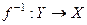 называется обратным к отображению
называется обратным к отображению 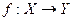 , если оно является и правым и левым обратным к
, если оно является и правым и левым обратным к 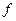 .
.
ЗАМЕЧАНИЕ 1) Отображение 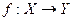 является инъективным тогда и только тогда, когда оно имеет левое обратное отображение.
является инъективным тогда и только тогда, когда оно имеет левое обратное отображение.
2) Отображение 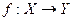 является сюръективным тогда и только тогда, когда оно имеет правое обратное отображение.
является сюръективным тогда и только тогда, когда оно имеет правое обратное отображение.
3) Отображение 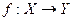 является биекцией тогда и только тогда, когда оно имеет обратное отображение.
является биекцией тогда и только тогда, когда оно имеет обратное отображение.
Определение Пусть 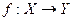 и
и 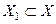 . Сужением отображения
. Сужением отображения 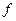 на подмноже ство
на подмноже ство 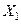 называется отображение
называется отображение 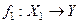 определяемое по правилу
определяемое по правилу
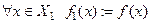 . Обозначение.
. Обозначение. 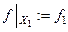 .
.
_____
Определение Выражение вида 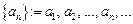 где числа
где числа 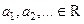 , называется числовой последовательностью.
, называется числовой последовательностью.
Определение Последовательность 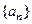 называется ограниченной, сверху (ограниченной снизу), если она имеет верхнюю грань:
называется ограниченной, сверху (ограниченной снизу), если она имеет верхнюю грань: 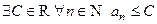 (нижнюю грань:
(нижнюю грань: 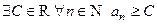 ). Последовательность
). Последовательность 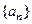 называется ограниченной, если она ограничена и сверху и снизу. В противном случае она называется неограниченной.
называется ограниченной, если она ограничена и сверху и снизу. В противном случае она называется неограниченной.
Определение Последовательность 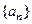 называется монотонно возрастающей (неубывающей), если
называется монотонно возрастающей (неубывающей), если 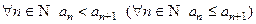 . Аналогично определяется монотонно убывающая (невозрастающая) последовательность.
. Аналогично определяется монотонно убывающая (невозрастающая) последовательность.
Определение Число 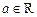 называется пределом последовательности
называется пределом последовательности 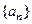 при
при 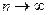 , если
, если 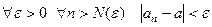 .
.
Определение Последовательность 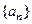 стремится к (плюс, минус) бесконечности
стремится к (плюс, минус) бесконечности
при 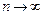 , если
, если 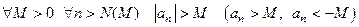 .
.
Обозначение 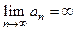 (
(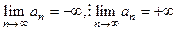 ).
).
Определение Последовательность, для которой существует конечный предел,
называется сходящейся. В противном случае она называется расходящейся.
Обозначение 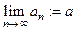 .
.
ТЕОРЕМА 1) (критерий Коши сходимости последовательности) Последователь ность 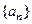 сходится тогда и только тогда, когда она фундаментальная:
сходится тогда и только тогда, когда она фундаментальная:
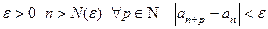 .
.
2) Если предел последовательности существует, то он единственен.
3) Если существует предел 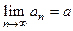 , то для любой подпоследовательности
, то для любой подпоследовательности 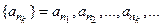 данной последовательности
данной последовательности 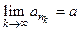 . Обратное утверждение, вообще говоря, неверно.
. Обратное утверждение, вообще говоря, неверно.
4) Сходящаяся последовательность ограничена.
5) Если последовательность не убывает (не возрастает) и ограничена сверху (снизу), то она является сходящейся.
Пусть 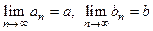 , причем
, причем 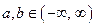 . Тогда справедливы следующие утверждения.
. Тогда справедливы следующие утверждения.
6) 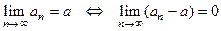 . 7) Если
. 7) Если 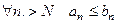 , то
, то 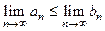 .
.
8) Пусть 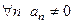 , Тогда
, Тогда 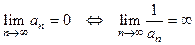 .
.
9) 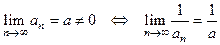 . 10)
. 10) 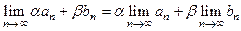 .
.
11) Если 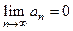 и последовательность
и последовательность 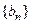 ограничена, то
ограничена, то 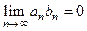 .
.
12) 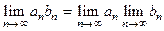 . 13) Если
. 13) Если 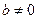 , то
, то 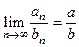 .
.
Определение Верхним (нижним) пределом последовательности 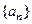 называется такое число
называется такое число 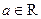
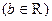 , что
, что 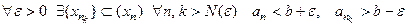 ,
,
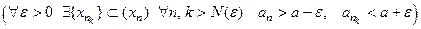
Обозначение 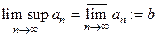 ,
, 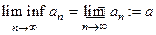 .
.
ЗАМЕЧАНИЕ 1) 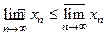 . 2)
. 2) 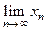 существует тогда и только тогда, когда
существует тогда и только тогда, когда 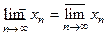 . 3)
. 3) 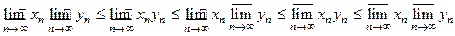 .4) Если
.4) Если 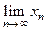 существует и
существует и 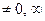 , то
, то 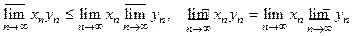 .
.
____
Определение Числовым рядом называется выражение вида 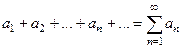 , где
, где 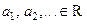 .
.
Определение Обобщенный гармонический ряд 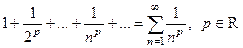 .
.
Определение Ряд 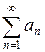 называется законоположительным (знакопостоянным),
называется законоположительным (знакопостоянным),
если 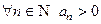 (
(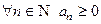 или
или 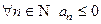 ).
).
Определение Ряд 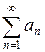 называется знакочередующимся, если
называется знакочередующимся, если 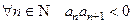 .
.
Определение 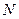 -ой частичной суммой ряда
-ой частичной суммой ряда 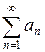 называется сумма
называется сумма 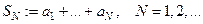 .
.
Определение Числовой ряд называется сходящимся, если существует конечный
предел 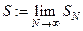 . Этот предел
. Этот предел 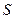 называется суммой ряда. Обозначение
называется суммой ряда. Обозначение 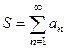 .
.
Определение Числовой ряд называется расходящимся, если 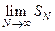 равен
равен 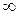 или не существует.
или не существует.
ТЕОРЕМА 1) (критерии Коши) Числовой ряд 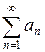 сходится тогда и только тогда,
сходится тогда и только тогда,
когда последовательность его частичных сумм 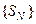 фундаментальная, то есть
фундаментальная, то есть
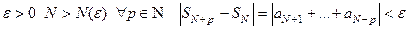 .
.
2) (необходимый признак сходимости) Если ряд 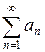 сходится, то
сходится, то 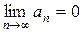 .
.
3) (достаточный признак расходимости) Если 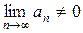 или не существует, то
или не существует, то
ряд 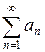 расходится. 4) (признак Лейбница) Если ряд
расходится. 4) (признак Лейбница) Если ряд 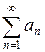 знакочередующийся и последовательность
знакочередующийся и последовательность 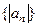 монотонно стремится к нулю:
монотонно стремится к нулю: 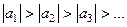 и
и 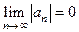 , то ряд сходится.
, то ряд сходится.
5) (признаки сравнения) Пусть 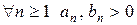 . Тогда: а) если
. Тогда: а) если 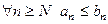 и
и 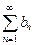 сходится, то
сходится, то 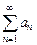 сходится; б) если
сходится; б) если 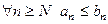 и
и 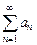 расходится, то
расходится, то 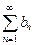 расходится; в) если существует
расходится; в) если существует 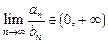 , то ряды
, то ряды 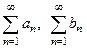 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
6) (признак Коши) Пусть 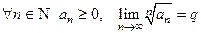 . Если
. Если 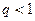 то ряд сходится
то ряд сходится 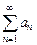 ; если
; если 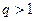 , то он расходится; если
, то он расходится; если 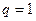 , то нужны дополнительные исследования.
, то нужны дополнительные исследования.
7) (Признак Даламбера) Пусть 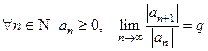 . Если
. Если 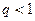 то ряд
то ряд 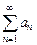 сходится; если
сходится; если 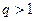 , то ряд расходится; если
, то ряд расходится; если 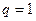 , то нужны дополнительные исследования.
, то нужны дополнительные исследования.
Определение Ряд 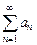 называется абсолютно сходящимся, если ряд из модулей
называется абсолютно сходящимся, если ряд из модулей
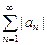 сходится.
сходится.
ЗАМЕЧАНИЕ Абсолютно сходящийся ряд сходится.
Определение Ряд 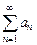 называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд 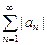 расходится.
расходится.
_____
Определение Пусть 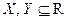 . Отображение
. Отображение 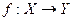 называется функцией одной переменной.
называется функцией одной переменной.
ЗАМЕЧАНИЕ Функция может быть задана тремя способами: таблично, аналитически (формулой) и графически.
Определение Функция 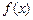 называется монотонно возрастающей (неубывающей) на
называется монотонно возрастающей (неубывающей) на 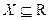 , если
, если 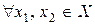 из
из 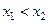 следует
следует 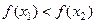 (
(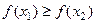 ).
).
Определение Функция 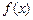 называется монотонно убывающей (не возрастающей) на
называется монотонно убывающей (не возрастающей) на 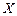 , если
, если 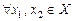 из
из 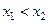 следует
следует 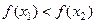 (
(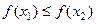 )ЗАМЕЧАНИЕ Если функция
)ЗАМЕЧАНИЕ Если функция 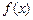 монотонна (то есть монотонно убывает или монотонно возрастает) на
монотонна (то есть монотонно убывает или монотонно возрастает) на 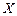 , то на множестве значений
, то на множестве значений 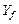 существует обратная функции
существует обратная функции 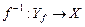 , которая также является монотонной. Обратное,вообще говоря, неверно.
, которая также является монотонной. Обратное,вообще говоря, неверно.
Определение Следующие 5 классов функций называются основными элементарными:
1) Степенные 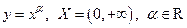 .
.
2) Показательные 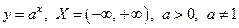 .
.
3) Логарифмические 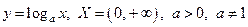 .
.
4) Тригонометрические 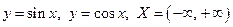 .
.
5) Обратные тригонометрические 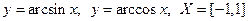 .
.
Определение Функция называется элементарной, если она получена из основных элементарных с помощью конечного числа, операций сложения, вычитания, умножения, деления, возведения в степень и композиции.
Определение Точка 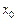 называется предельной точкой множества
называется предельной точкой множества  , если в каждой
, если в каждой 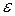 - окрестности
- окрестности 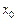 существуют точки из
существуют точки из  , отличные от
, отличные от 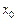 .
.
Определение Пусть функция 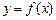 определена на
определена на и
и 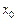 - предельная точка мно
- предельная точка мно
жества  . Говорят что
. Говорят что 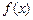 стремится к числу
стремится к числу 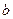 (имеет пределом число
(имеет пределом число 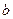 ), когда
), когда
переменная 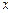 стремится к числу
стремится к числу 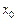 , если
, если
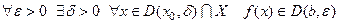 .
.
Обозначение 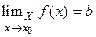 или
или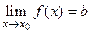 , если
, если  определена на некоторой проколотой окрестности точки
определена на некоторой проколотой окрестности точки 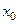 .
.
ЗАМЕЧАНИЕ Если 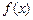 определена на множестве
определена на множестве 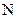 и
и 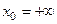 , то данное определение предела совпадет с определением предела последовательности
, то данное определение предела совпадет с определением предела последовательности
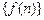 :
: 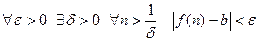 .
.
Определение Пусть функция 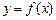 определена на
определена на  и
и 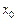 - предельная точка
- предельная точка
множества  . Говорят что функция
. Говорят что функция  имеет предел
имеет предел 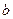 справа (слева) в точке
справа (слева) в точке
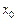 , если
, если 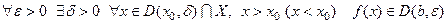 .
.
Обозначение 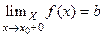 (
(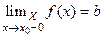 ) или
) или 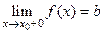 (
(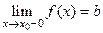 ).
).
Определение Функция  ограничена сверху (снизу) на множестве
ограничена сверху (снизу) на множестве  , если
, если 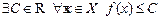 (
(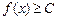 ). Функция
). Функция  ограничена на
ограничена на  , если она ограничена на нем и сверху и снизу. Функция
, если она ограничена на нем и сверху и снизу. Функция  ограничена при
ограничена при 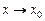 , если она ограничена на некоторой окрестности
, если она ограничена на некоторой окрестности 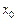 (то есть
(то есть 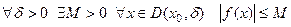 ).
).
ЗАМЕЧАНИЕ Ограниченная на множестве функция будет ограниченной при 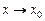 . Обратное, вообще говоря, неверно.
. Обратное, вообще говоря, неверно.
ТЕОРЕМА 1) (лемма Гейне) 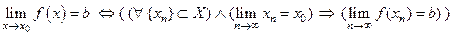 .
.
2) Если существует 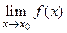 , то он единственный.
, то он единственный.
3) Если  монотонна и ограничена на
монотонна и ограничена на  , то существует конечный предел
, то существует конечный предел 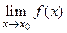 .
.
4) 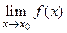 существует тогда и только тогда, когда существуют пределы функции справа и слева в этой точке и они равны.
существует тогда и только тогда, когда существуют пределы функции справа и слева в этой точке и они равны.
Пусть существуют конечные пределы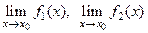 . Тогда 5)
. Тогда 5) 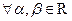
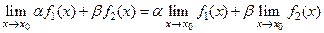 . 6)
. 6) 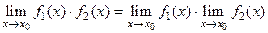 .
.
7)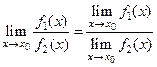 , если
, если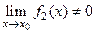 . 8) Если
. 8) Если 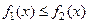 , то
, то 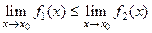
_____
Определение Функция  называется бесконечно малой (БМ) при
называется бесконечно малой (БМ) при 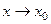 , если
, если
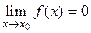 . Обозначение
. Обозначение 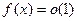 .
.
ЗАМЕЧАНИЕ 1) 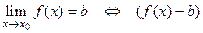 - БМ.
- БМ.
2) Если 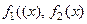 БМ, то
БМ, то 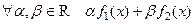 есть БМ.
есть БМ.
3) Если 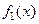 - БМ, а
- БМ, а 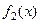 ограниченная функция при
ограниченная функция при 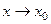 , то
, то 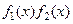 есть БМ.
есть БМ.
4) Если 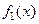 - БМ, а
- БМ, а 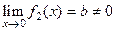 , то
, то 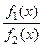 - БМ при
- БМ при 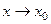 .
.
Определение Бесконечно малая 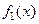 имеют порядок убывания не выше (выше),
имеют порядок убывания не выше (выше),
чем бесконечно малая 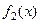 , если функция
, если функция 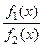 ограничена при
ограничена при 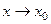
(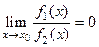 ). Обозначения
). Обозначения 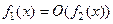 (
(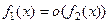 ).
).
Определение Бесконечно малые 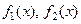 называется эквивалентными при
называется эквивалентными при 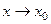 , если
, если 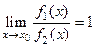 . Обозначение
. Обозначение 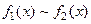 .
.
ЗАМЕЧАНИЕ Под знаком предела бесконечно малые множители можно заменять на эквивалентные, а бесконечно малые слагаемые, вообще говоря, нельзя.
Определение Функция  называется бесконечно большой (ББ) при
называется бесконечно большой (ББ) при 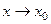 , если
, если 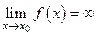 .
.
ЗАМЕЧАНИЕ Функция  есть ББ при
есть ББ при 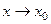 тогда и только тогда, когда функция
тогда и только тогда, когда функция 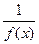 есть БМ при
есть БМ при 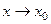 .
.
_____
Определение Функцией эн-факториал называется функция, определенная на множестве целых неотрицательных чисел по правилу 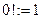 ,
, 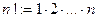 . Пусть
. Пусть 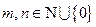 ,
, 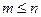 . Числом сочетаний из
. Числом сочетаний из 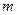 по
по 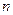 называется величина
называется величина
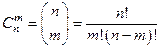 .
.
ТЕОРЕМА 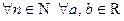
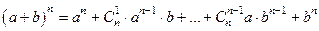 .
.
СЛЕДСТВИЕ Последовательность 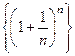 имеет конечный предел.
имеет конечный предел.
ЗАМЕЧАНИЕ 1 Можно доказать, что число 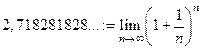 иррациональное. Его обозначают буквой
иррациональное. Его обозначают буквой 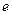 .
.
ЗАМЕЧАНИЕ 2 Существует 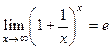 , который называется вторым
, который называется вторым
замечательным пределом.
Определение Натуральным логарифмом числа 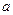 называется число
называется число 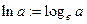 .
.
СЛЕДСТВИЕ 1 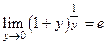 . СЛЕДСТВИЕ 2
. СЛЕДСТВИЕ 2 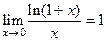 .
.
СЛЕДСТВИЕ 3 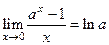 .
.
_____
Определение Пусть функция 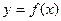 определена на
определена на 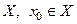 и является предельной точкой
и является предельной точкой  . Говорят, что
. Говорят, что  непрерывна в точке
непрерывна в точке 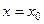 , если существует предел
, если существует предел 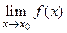 и он равен
и он равен 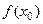 .
.
ЗАМЕЧАНИЕ Функция  непрерывна в точке
непрерывна в точке 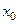 тогда и только тогда, когда
тогда и только тогда, когда
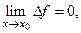 где
где 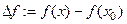 - приращение функции
- приращение функции  в точке
в точке 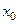 .
.
Определение Функция  называется непрерывной на множестве
называется непрерывной на множестве  , если она
, если она
непрерывна в каждой точке этого множества.
ЗАМЕЧАНИЕ Элементарная функция непрерывна на каждом интервале, на котором она определена.
Определение Пусть 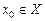 и является предельной точкой.
и является предельной точкой. 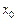 называется точкой устранимого разрыва, если существует конечный
называется точкой устранимого разрыва, если существует конечный 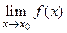 и он
и он 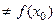 .
.
Определение 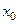 называется точкой разрыва первого рода, если существуют конечные пределы справа и слева, но они различны.
называется точкой разрыва первого рода, если существуют конечные пределы справа и слева, но они различны.
_____
Определение Точка множества  , в которой
, в которой  достигает своего наибольшего (наименьшего) значения, называется точкой максимума (минимума) функции. При этом значение функции в этой точке называется максимумом (минимумом) функции. Точки максимума и минимума называются точками экстремума, а максимум или минимум – экстремумом функции.
достигает своего наибольшего (наименьшего) значения, называется точкой максимума (минимума) функции. При этом значение функции в этой точке называется максимумом (минимумом) функции. Точки максимума и минимума называются точками экстремума, а максимум или минимум – экстремумом функции.
Обозначение 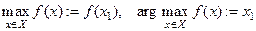
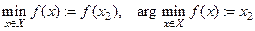 .
.
ТЕОРЕМА (свойства непрерывных функций) 1) Линейная комбинация непрерывных функций есть функция непрерывная. 2) Произведение непрерывных функций есть функция непрерывная. 3) Частное непрерывных функций есть функция непрерывная в точках, где знаменатель не равен 0. 4) Композиция непрерывных функций есть функция непрерывная. 5) Непрерывная на отрезке 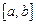 функция достигает на нём своих наибольшего и наименьшего значений. 6) Если
функция достигает на нём своих наибольшего и наименьшего значений. 6) Если  непрерывна на
непрерывна на 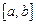 и
и 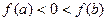 , то
, то 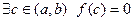
СЛЕДСТВИЕ Если  непрерывна на
непрерывна на 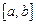 , то
, то
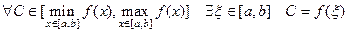 .
.
ЗАМЕЧАНИЕ Пусть  монотонно возрастает (убывает) на
монотонно возрастает (убывает) на 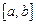 .
.  непрерывна на
непрерывна на 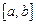 тогда и только тогда, когда
тогда и только тогда, когда 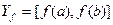 (
(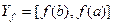 ).
).
Определение  называется равномерно непрерывной на
называется равномерно непрерывной на  , если
, если
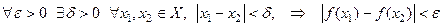 .
.
ЗАМЕЧАНИЕ 1) Равномерно непрерывная на  функция будет непрерывной на
функция будет непрерывной на  . Обратное, вообще говоря, не верно. 2) Если
. Обратное, вообще говоря, не верно. 2) Если  непрерывна на
непрерывна на 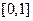 , то она равномерно непрерывна на нем.
, то она равномерно непрерывна на нем.
Определение Методы решения нелинейного уравнения 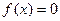 , где функция
, где функция  непрерывна, называются методами нулевого порядка (методами одномерной оптимизации).
непрерывна, называются методами нулевого порядка (методами одномерной оптимизации).
АЛГОРИТМ метода деления отрезка пополам.
 2014-02-09
2014-02-09 800
800








