Определение Матрицей размера 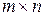 называется совокупность чисел, расположенных в виде таблицы из m строк и n столбцов.
называется совокупность чисел, расположенных в виде таблицы из m строк и n столбцов.
Обозначение 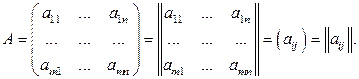
Определение Матрицы 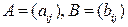 называются равными,
называются равными, 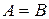 , если они имеют одинаковые размеры и
, если они имеют одинаковые размеры и 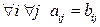 .
.
Определение Матрица называется квадратной, если 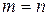 .
.
Определение Диагональ квадратной матрицы, начинающаяся в левом верхнем, и оканчивающаяся в правом нижнем углу, называется главной; вторая диагональ – неглавная.
Определение Квадратная матрица называется единичной, если все числа на главной диагонали равны 1, а все числа вне главной диагонали равны 0.
Определение Матрица называется нулевой (нуль-матрица), если все ее элементы равны 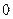 .
.
Определение Суммой двух матриц 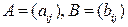 размера
размера 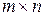 называется матрица
называется матрица 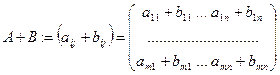 .
.
Определение Произведением матрицы 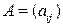 на число
на число 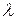 называется матрица
называется матрица 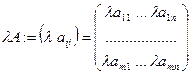 .
.
Определение Произведением матрицы 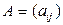 размера
размера 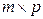 на матрицу
на матрицу 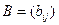 размера
размера 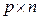 называется матрица
называется матрица 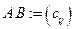 размера
размера 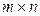 , элементы которой вычисляются по правилу
, элементы которой вычисляются по правилу 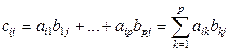 .
.
Определение Квадратная матрица 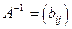 размера
размера 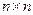 называется обратной к квадратной матрице
называется обратной к квадратной матрице 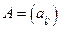 размера
размера 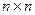 , если
, если 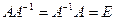 .
.
_____
Определение 1 Определителем (детерминантом) первого порядка квадратной матрицы 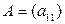 размера
размера 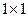 называется число
называется число 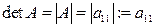 .
.
Определение 2 Определителем 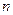 -го порядка квадратной матрицы
-го порядка квадратной матрицы 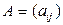 разме
разме
ра 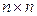 называется число
называется число
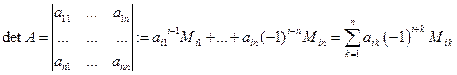 ,
,
где 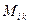 - определитель
- определитель 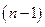 -го порядка матрицы, которая получается
-го порядка матрицы, которая получается
вычеркиванием из матрицы 
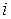 -той строки и
-той строки и 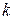 -го столбца.
-го столбца.
ЗАМЕЧАНИЕ Данная формула вычисления называется разложением определителя по 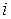 - ой строке. Формула разложения по
- ой строке. Формула разложения по 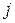 - ому столбцу имеет вид
- ому столбцу имеет вид
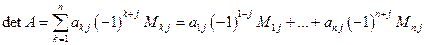 .
.
ТЕОРЕМА 1) Если в определителе поменялись местами две строки (два столбца), то новый определитель будет отличаться от исходного только знаком.
2) Если элементы одной строки (или столбца) умножить на одно и тоже число λ, то полученный новый определитель будет в λ раз больше исходного.
3) Если к одной строке (столбцу) прибавить поэлементно другую строку (столбец), то полученный новый определитель совпадет с исходным.
4) Пусть два определителя одинакового порядка различаются только одной строкой (столбцом). Тогда их сумма совпадает с определителем, у которого соответствующая строка (столбец) есть сумма строк (столбцов) слагаемых определителей.
Определение Минором порядка 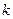 матрицы
матрицы  называется определитель матрицы, элементы которой стоят на пересечении каких-либо
называется определитель матрицы, элементы которой стоят на пересечении каких-либо 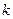 строк и
строк и 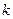 столбцов матрицы
столбцов матрицы  .
.
Определение Рангом матрицы называется самый большой порядок у не равных нулю миноров этой матрицы. Обозначение 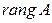 .
.
Определение Квадратная матрица А называется невырожденной, если 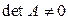 , то есть когда
, то есть когда 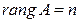 .
.
Определение Матрица 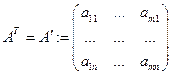 называется транспонированной к матрице
называется транспонированной к матрице 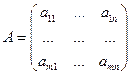 .
.
Определение Число 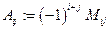 называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента 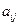 матрицы
матрицы  , а матрица
, а матрица 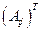 - присоединенной матрицей к матрице
- присоединенной матрицей к матрице  .
.
ЗАМЕЧАНИЕ Если матрица  не вырождена, то существует обратная матрица
не вырождена, то существует обратная матрица 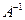 , которая вычисляется по формуле
, которая вычисляется по формуле 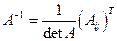 .
.
_____
Определение Системой линейных алгебраических уравнений (СЛАУ)
называется система уравнений вида 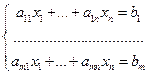 , где известные числа
, где известные числа 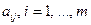 , называются коэффициентами СЛАУ; известные числа
, называются коэффициентами СЛАУ; известные числа 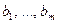 - свободными членами; неизвестные, искомые числа
- свободными членами; неизвестные, искомые числа 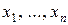 - решением СЛАУ.
- решением СЛАУ.
Обозначения 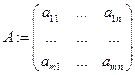 - матрица коэффициентов;
- матрица коэффициентов; 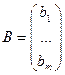 - матрица свободных членов;
- матрица свободных членов; 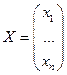 - матрица неизвестных;
- матрица неизвестных; 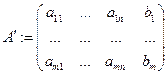 - расширенная матрица СЛАУ.
- расширенная матрица СЛАУ.
Эти обозначения позволяют записать СЛАУ в матричном виде 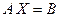 .
.
Определение Решить СЛАУ – это значит найти все ее решения.
Определение СЛАУ называется совместной, если она имеет хотя бы одно решение. В противном случае СЛАУ несовместна.
Определение Две СЛАУ одинакового порядка называются эквивалентными, если они
обе несовместны или обе совместны и имеют одинаковое множество решений.
ЗАМЕЧАНИЕ СЛАУ переходит в эквивалентную при следующих элементарных преобразованиях: 1) перестановка местами двух уравнений,
2) умножение какого-либо уравнения на неравное нулю число,
3) поэлементное прибавление к одному уравнению другого уравнения.
Определение СЛАУ называется определенной, если она имеет ровно одно решение и неопределенной, если решений больше одного.
ТЕОРЕМА 1) (критерий Кронекера-Капелли совместности СЛАУ) СЛАУ совместна тогда и только тогда, когда ранг матрицы этой СЛАУ равен рангу расширенной матрицы.
2) (критерий определенности СЛАУ) Для того чтобы СЛАУ была определенной необходимо и достаточно, чтобы она была совместной и ранг матрицы коэффициентов совпадал с числом неизвестных: 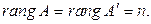
3) (формулы Крамера) Определенная СЛАУ с помощью элементарных преобразований приводится к СЛАУ, у которой матрица коэффициентов 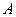 квадратная и
квадратная и 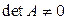 . В этом случае решение СЛАУ вычисляется по формулам Крамера
. В этом случае решение СЛАУ вычисляется по формулам Крамера 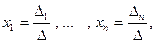 где
где 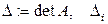 -определитель, получаемый из
-определитель, получаемый из 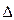 заменой i-ого столбца на столбец свободных членов.
заменой i-ого столбца на столбец свободных членов.
СЛЕДСТВИЕ СЛАУ с 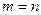 будет определенной тогда и только тогда, когда
будет определенной тогда и только тогда, когда 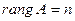
Определение Элементарными преобразованиями матрицы называются
следующие: 1) перестановка двух строк;
2) поэлементное умножение какой-либо строки на неравное нулю число;
3) прибавление к одной строке соответствующих элементов другой строки.
ЗАМЕЧАНИЕ СЛАУ преобразуется в эквивалентную, если ее расширенную матрицу подвергнуть элементарным преобразованиям.
Определение Методом Гаусса называется метод решения СЛАУ с помощью элементарных преобразований по следующему правилу.
АЛГОРИТМ Сначала обнуляются все элементы, стоящих ниже главной
диагонали последовательно по столбцам, начиная с первого; затем обнуляют
элементы над диагональю последовательно по столбцам, начиная с 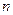 -го.
-го.
_____
Определение Векторным (линейным) пространством называется множество Е, для элементов которого определены операции сложения и умножения на число, удовлетворяющие следующим аксиомам:
1)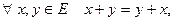
2)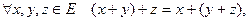
3)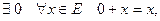
4) 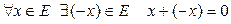 ,
,
5) 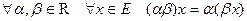 ,
,
6) 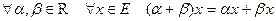 ,
,
7) 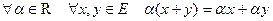 ,
,
8)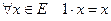 .
.
Определение Линейной комбинацией (линейной алгебраической суммой) элементов 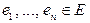 называется сумма вида
называется сумма вида 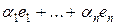 , где
, где 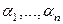 - действительные числа, которые называются коэффициентами разложения.
- действительные числа, которые называются коэффициентами разложения.
Определение Элементы 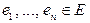 называются линейно зависимыми, если существует равная нулю линейная комбинация этих элементов, в которой не все коэффициенты равны нулю. В противном случае элементы называются линейно независимыми.
называются линейно зависимыми, если существует равная нулю линейная комбинация этих элементов, в которой не все коэффициенты равны нулю. В противном случае элементы называются линейно независимыми.
СЛЕДСТВИЕ Элементы линейно зависимы тогда и только тогда, когда хотя бы один из них представим в виде линейной комбинации остальных.
Определение Последовательность элементов 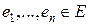 называется полной (базисом) в векторном пространстве
называется полной (базисом) в векторном пространстве 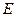 если каждый элемент из Е (единственным образом) представим в виде линейной комбинации этих элементов.
если каждый элемент из Е (единственным образом) представим в виде линейной комбинации этих элементов.
ТЕОРЕМА 2.3 1) Последовательность 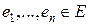 является базисом в векторном пространстве тогда и только тогда, когда элементы
является базисом в векторном пространстве тогда и только тогда, когда элементы 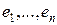 линейно независимы и каждый элемент из
линейно независимы и каждый элемент из 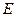 представим в виде их линейной комбинации.
представим в виде их линейной комбинации.
2) Базисы в векторном пространстве имеют одинаковое число элементов.
Определение Если в векторном пространстве существует базис, то число элементов 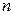 этого базиса называется размерностью пространства Е, а пространство называется
этого базиса называется размерностью пространства Е, а пространство называется 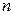 - мерным. Обозначение.
- мерным. Обозначение. 
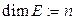 .
.
Определение Векторное пространство Е называется бесконечномерным, если в нём не существует базис с конечным числом элементов.
Определение Декартовым произведением векторных пространств E и F называется декартово произведение соответствующих множеств 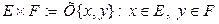 , на котором определены операции сложения элементов и умножения их на число по правилу:
, на котором определены операции сложения элементов и умножения их на число по правилу:
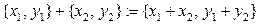 ,
, 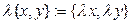 .
.
ЗАМЕЧАНИЕ 1 Введенные операции на декартовом произведении удовлетворяют 8 аксиомам.
ЗАМЕЧАНИЕ 2 Аналогично определяются декартовы произведения 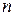 пространств
пространств 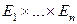 и
и 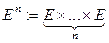 .
.
5 развернутых важных примеров векторных пространств.
ПРИМЕР 1 Пространство векторов с общим началом 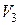 .
.
ПРИМЕР 2 Пространство комплексных чисел  .
.
Определение Символ вида 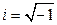 , обладающий свойством
, обладающий свойством 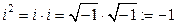 , называется мнимой единицей.
, называется мнимой единицей.
Определение Выражение вида 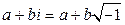 , где
, где 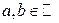 , называется комплексным числом (в алгебраической форме).
, называется комплексным числом (в алгебраической форме).
Обозначение Комплексное число традиционно обозначается буквой 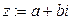 ; множество комплексных чисел обозначается
; множество комплексных чисел обозначается 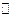 .
.
Определение Вещественное число 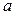 называется действительной частью комплексного числа
называется действительной частью комплексного числа 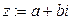 , а вещественное число
, а вещественное число 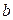 называется коэффициентом мнимой части
называется коэффициентом мнимой части 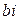 комплексного числа.
комплексного числа.
Обозначение 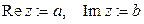 .
.
Определение Комплексные числа 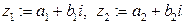 , называются равными, если равны их действительные и мнимые части:
, называются равными, если равны их действительные и мнимые части: 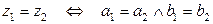 .
.
Определение Число вида 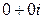 называется нулём (комплексным) и кратко обозначается
называется нулём (комплексным) и кратко обозначается 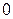 . Вместо
. Вместо 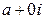 обычно пишут просто
обычно пишут просто 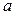 .
.
Определение Суммой комплексных чисел 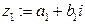 ,
, 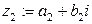 называется комплексное число
называется комплексное число 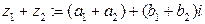 .
.
Следующее определение несколько более общее, чем требуется в этом примере.
Определение Произведением комплексных чисел 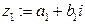 ,
, 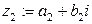 называется комплексное число
называется комплексное число 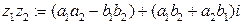 .
.
ЗАМЕЧАНИЕ 1 Множество комплексных чисел  удовлетворяяет аксиомам 1)-8) векторного пространства относительно операций сложения и умножения на действительной число. Две аксиомы мы уже проверили.
удовлетворяяет аксиомам 1)-8) векторного пространства относительно операций сложения и умножения на действительной число. Две аксиомы мы уже проверили.
ЗАМЕЧАНИЕ 2 Вещественная и мнимая единицы 1, 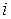 образуют базис в
образуют базис в  . Поэтому
. Поэтому 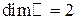 .
.
ЗАМЕЧАНИЕ 3 В определении векторного пространство элементы умножаются на действительные числа. Аналогично определяется векторное пространство, в котором элементы умножаются на комплексные числа. В этом случае говорят о векторном пространстве над полем комплексных чисел (комплексном пространстве).
ПРИМЕР 3 Пространство 
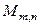 матриц размера
матриц размера 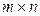 .
.
Определения равенства матриц, нулевой матрицы, суммы матриц и произведения
матриц на число мы уже давали. Из восьми аксиом проверим для множества
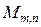 , например, четвертую. Матрица
, например, четвертую. Матрица 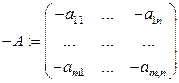 является
является
противоположной к матрице 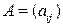 .
.
Действительно, 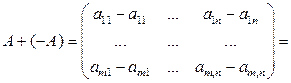
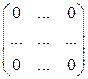 - нуль-матрица.
- нуль-матрица.
ЗАМЕЧАНИЕ Попарно различные матрицы размера 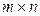 в количестве
в количестве 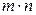
штук, у каждой из которых один элемент равен 1, а остальные равны 0, образуют
базис в пространстве 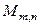 .
.
ПРИМЕР 4 Пространство 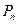 многочленов степени
многочленов степени 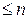 .
.
Определение Многочленом степени 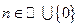 называется функция вида
называется функция вида 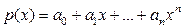 , где
, где 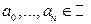 (или
(или 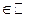 ), причем
), причем 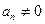 . То есть многочлен является линейной комбинацией степеней
. То есть многочлен является линейной комбинацией степеней 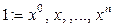
Определение Многочлены 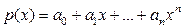 ,
, 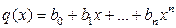 называются равными, если у них совпадают коэффициенты при одинаковых степенях
называются равными, если у них совпадают коэффициенты при одинаковых степенях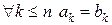
Определение Многочлен 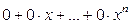 называется нулевым (нулем в простран стве)
называется нулевым (нулем в простран стве) 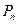 и обозначается
и обозначается 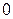 .
.
Определение Суммой многочленов 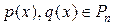 называется многочлен
называется многочлен 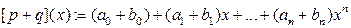 .
.
Определение Произведением числа 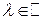 на многочлен
на многочлен 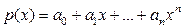
называется многочлен 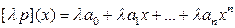 .
.
ЗАМЕЧАНИЕ 1 Множество 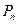 удовлетворяет аксиомам 1)-8), и потому является векторным пространством.
удовлетворяет аксиомам 1)-8), и потому является векторным пространством.
ЗАМЕЧАНИЕ 2 Последовательность многочленов 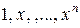 является базисом в
является базисом в 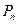 . Поэтому
. Поэтому 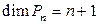 .
.
ПРИМЕР 5 Арифметическое пространство 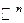 .
.
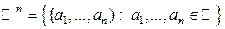 мы обозначили множество упорядоченных
мы обозначили множество упорядоченных 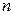 -ок действительных чисел.
-ок действительных чисел.
Определение Две 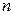 -ки
-ки 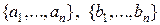 называются равными, если числа, стоящие на одинаковых местах, совпадают:
называются равными, если числа, стоящие на одинаковых местах, совпадают: 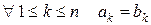 .
.
Определение Нулём в 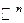 называется
называется 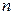 - ка вида
- ка вида 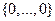 .
.
Определение Суммой двух 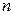 - ок
- ок 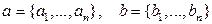 называется
называется 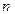 - ка
- ка 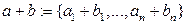 .
.
Определение Произведением числа 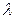 на
на 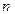 - ку
- ку 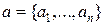 называется
называется 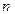 - ка
- ка
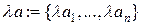 .
.
ЗАМЕЧАНИЕ 1 Множество 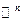 удовлетворяет аксиомам 1)-8), и потому является векторным пространством.
удовлетворяет аксиомам 1)-8), и потому является векторным пространством.
ЗАМЕЧАНИЕ 2 Элементы 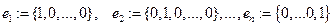
образуют базис в 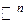 . Следовательно,
. Следовательно, 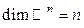 .
.
ЗАМЕЧАНИЕ 3 Множества чисел 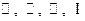 не являются векторными пространствами.
не являются векторными пространствами.
_____
Определение Отображением множества 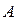 в множество
в множество 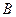 называется правило, сопоставляющее каждому элементу из
называется правило, сопоставляющее каждому элементу из 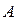 один элемент из
один элемент из 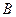 . В случае
. В случае 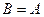 отображение называется преобразованием.
отображение называется преобразованием.
Обозначение Правило обозначается латинскими буквами. Например, 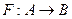 .
.
Определение Множество 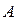 называется областью определения отображения
называется областью определения отображения 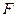 ;
;
множество 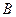 - областью значений отображения; множество
- областью значений отображения; множество
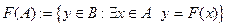 - множеством значений (образом отображения)
- множеством значений (образом отображения) 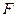 .
.
Определение Отображение 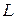 из векторного пространства
из векторного пространства 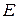 в векторное пространство
в векторное пространство 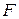 называется линейным оператором (отображением), если
называется линейным оператором (отображением), если
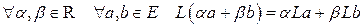 .
.
Определение Линейный оператор 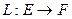 называется изоморфизмом векторных пространств
называется изоморфизмом векторных пространств 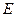 и
и 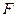 , если он переводит разные элементы в разные:
, если он переводит разные элементы в разные: 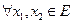
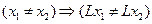 , и каждый элемент из
, и каждый элемент из 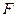 является образом некоторого элемента из
является образом некоторого элемента из 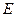 :
: 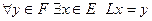 . При этом пространства
. При этом пространства 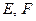 называются изоморфными.
называются изоморфными.
ЗАМЕЧАНИЕ 1 Это понятие позволяет формулировать результаты для векторного пространства на языке изоморфного ему пространства. Иногда это оказывается удобным.
Определение Линейный оператор из 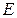 в
в 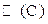 называется линейной формой (линейным функционалом).
называется линейной формой (линейным функционалом).
Определение Отображение 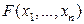 из векторного пространства
из векторного пространства 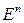 в вектор ное пространство
в вектор ное пространство 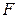 называется
называется 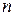 - линейным полилинейным) отображением, если оно является линейным отображением из
- линейным полилинейным) отображением, если оно является линейным отображением из 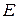 в
в 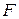 по каждой переменной
по каждой переменной 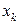 ,
, 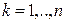 , при фиксированных остальных.
, при фиксированных остальных.
Определение 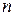 - линейное отображение из
- линейное отображение из 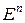 в
в 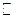 называется
называется 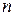 - линейной (полилинейной) формой.
- линейной (полилинейной) формой.
ЗАМЕЧАНИЕ 2 - линейное отображение 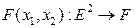 принято называть билинейным отображением.
принято называть билинейным отображением.
Определение Билинейная форма 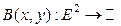 называется скалярным произведением на векторном пространстве
называется скалярным произведением на векторном пространстве 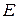 , если она обладает свойствами:
, если она обладает свойствами:
1) 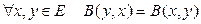 ; 2)
; 2) 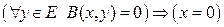 ; 3)
; 3) 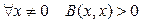
Обозначение 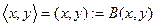 .
.
Определение Отображение 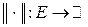 , называется нормой, если оно обладает
, называется нормой, если оно обладает
свойствами:
1)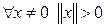 ; 2)
; 2) 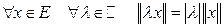 ; 3)
; 3) 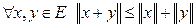 .
.
ЗАМЕЧАНИЕ 1 Понятие нормы, как нетрудно заметить по свойствам, обобщает понятие длины вектора в 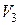 .
.
ЗАМЕЧАНИЕ 2 Каждое скалярное произведение 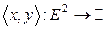 порождает норму в
порождает норму в 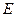 по правилу
по правилу 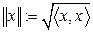 .
.
СЛЕДСТВИЕ Естественное скалярное произведение в 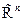 обладает свойством
обладает свойством 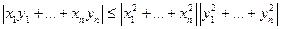 .
.
Определение 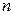 -мерным евклидовым (точечным) пространством называется тройка объектов:
-мерным евклидовым (точечным) пространством называется тройка объектов: 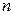 -мерное векторное пространство
-мерное векторное пространство 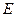 , какое-либо скалярное произведение
, какое-либо скалярное произведение 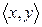 на нём и множество “точек”
на нём и множество “точек” 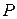 , которые согласованы следующим образом:
, которые согласованы следующим образом:
1) каждой упорядоченной паре точек 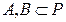 поставлен в соответствие один элемент
поставлен в соответствие один элемент
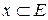 , который обозначают
, который обозначают 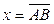 ; 2)
; 2) 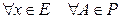 существует единственная точка
существует единственная точка 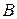 со свойством
со свойством 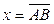 ; 3)
; 3) 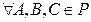
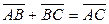 .
.
Обозначение 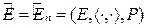 .
.
Определение Расстоянием между двумя точками 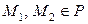 называется число
называется число
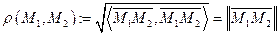 .
.
Определение 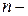 мерным аффинным пространством называется пара
мерным аффинным пространством называется пара 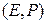 со свойствами 1) -3).
со свойствами 1) -3).
Определение 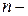 мерным евклидовым векторным пространством называется пара
мерным евклидовым векторным пространством называется пара 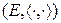 .
.
Определение 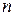 - мерным арифметическим евклидовым пространством
- мерным арифметическим евклидовым пространством 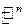 называет ся тройка объектов: арифметическое пространство
называет ся тройка объектов: арифметическое пространство 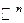 , естественное скалярное произведение
, естественное скалярное произведение 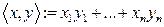 и множество ”точек”
и множество ”точек” 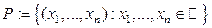 . При этом точки
. При этом точки 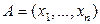 ,
, 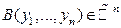 свяжем с вектором из
свяжем с вектором из 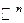 по правилу
по правилу 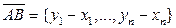 . Тогда расстояние между точками
. Тогда расстояние между точками 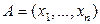 ,
, 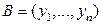
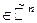 вычисляется по формуле
вычисляется по формуле
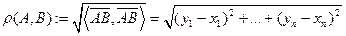 .
.
____
Определение В 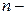 мерном евклидовом пространстве
мерном евклидовом пространстве 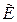 совокупность каких-либо точки
совокупность каких-либо точки 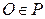 и базиса
и базиса 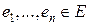 называется декартовой системой координат (ДСК).
называется декартовой системой координат (ДСК).
Определение Символом Кронекера называется отображение 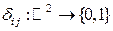 , определяемое по правилу
, определяемое по правилу 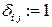 , если
, если 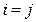 и
и 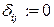 , если
, если 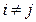 .
.
Определение Базис называется ортонормированным, если 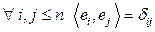 .
.
ЗАМЕЧАНИЕ Элементы 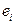 такого базиса попарно перпендикулярны:
такого базиса попарно перпендикулярны:
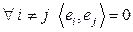 и их нормы равны единице:
и их нормы равны единице: 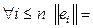
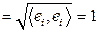 . Здесь аналогия со школой, когда равенство нулю скалярного произведения означало ортогональность векторов, а квадрат модуля вектора совпадал со скалярным произведением вектора на себя.
. Здесь аналогия со школой, когда равенство нулю скалярного произведения означало ортогональность векторов, а квадрат модуля вектора совпадал со скалярным произведением вектора на себя.
Определение ДСК, в которой выделенный базис является ортонормированным, называется прямоугольной декартовой системой координат (ПДСК).
ЗАМЕЧАНИЕ Всюду ниже ДСК предполагается прямоугольной, если не оговорено противное.
Определение Коэффициенты разложения элемента 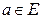 по базису
по базису 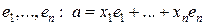 , называются, как и ранее, координатами (компонентами) вектора
, называются, как и ранее, координатами (компонентами) вектора 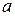 в базисе
в базисе 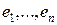 .
.
Обозначение 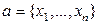 . Это обозначение объясняется изоморфизмом между пространствами
. Это обозначение объясняется изоморфизмом между пространствами 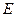 и
и 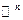 , устанавливаемым линейным оператором
, устанавливаемым линейным оператором 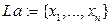 , где
, где 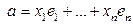 .
.
Определение Радиусом-вектором точки 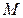 и ПДСК называется вектор
и ПДСК называется вектор 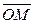 .
.
Определение Координатами точки 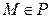 в ПДСК называются компоненты её радиуса-вектора
в ПДСК называются компоненты её радиуса-вектора 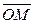 .
.
Обозначение Если 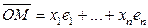 , то
, то 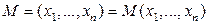 .
.
Определение Пусть дана матрица 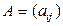 размера
размера 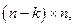
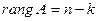 и последовательность чисел
и последовательность чисел 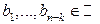 .
. 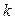 -мерной плоскостью в
-мерной плоскостью в 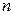 -мерном евклидовом пространстве
-мерном евклидовом пространстве 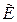 с фиксированной ПДСК называется множество точек
с фиксированной ПДСК называется множество точек 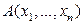 , координаты которых удовлетворяют СЛАУ
, координаты которых удовлетворяют СЛАУ 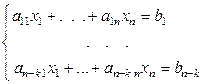 .
.
Определение Прямой в 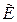 называется
называется 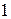 -плоскость.
-плоскость.
Определение Полярной системой координат в 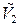 называется совокупность точки
называется совокупность точки 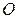 (-полюс) и луча с началом в этой точке (-полярная ось).
(-полюс) и луча с началом в этой точке (-полярная ось).
Определение Полярными координатами точки 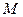 называется пара чисел
называется пара чисел 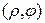 , где
, где 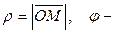 угол между полярной осью и вектором
угол между полярной осью и вектором 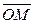 , отсчитываемый против часовой стрелки.
, отсчитываемый против часовой стрелки.
ЗАМЕЧАНИЕ 1 Каждая точка евклидовой плоскости 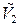 вполне определяется заданием полярных координат.
вполне определяется заданием полярных координат.
ЗАМЕЧАНИЕ 2 Совместим прямоугольную декартову и полярную системы координат так, чтобы начало координат совпадало с полюсом, а ось 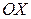 - с полярной осью Тогда декартовы координаты
- с полярной осью Тогда декартовы координаты 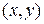 точки
точки 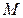 и ее полярные координаты связаны, как легко усмотреть из рисунка, равенствами
и ее полярные координаты связаны, как легко усмотреть из рисунка, равенствами
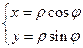 ,
, 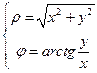 .
.
Определение В 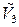 с ПДСК фиксируем точку
с ПДСК фиксируем точку 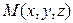 . Тройка чисел
. Тройка чисел 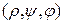 , где
, где 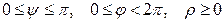 , называется сферическими координатами точки
, называется сферическими координатами точки 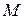 .
.
ЗАМЕЧАНИЕ 1 Каждая точка 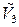 вполне определяется своими сферическими координатами.
вполне определяется своими сферическими координатами.
ЗАМЕЧАНИЕ 2 Так как 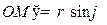 , то декартовы и сферические координаты точки
, то декартовы и сферические координаты точки 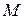 связаны равенствами
связаны равенствами 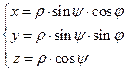 .
.
Определение В 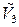 с ПДСК фиксируем точку
с ПДСК фиксируем точку 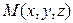 . Тройка чисел
. Тройка чисел 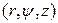 , где
, где 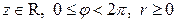 называется цилиндрическими координатами точки
называется цилиндрическими координатами точки 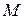 .
.
ЗАМЕЧАНИЕ 1 Каждая точка 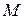 вполне определяется своими цилиндрическими координатами.
вполне определяется своими цилиндрическими координатами.
ЗАМЕЧАНИЕ 2 В ПДСК декартовы и цилиндрические координаты точки 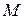 связаны равенствами:
связаны равенствами: 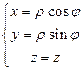 .
.
_____
Определение Пусть даны ось 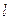 (
(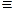 направленная прямая) и вектор
направленная прямая) и вектор 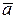 . Опустим перпендикуляры из его концов на ось. Проекцией вектора
. Опустим перпендикуляры из его концов на ось. Проекцией вектора 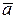 на ось
на ось 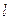 называется расстояние между основаниями этих перпендикуляров, взятое со знаком "+", если
называется расстояние между основаниями этих перпендикуляров, взятое со знаком "+", если 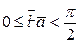 , со знаком "-", если
, со знаком "-", если 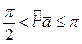 и равное нулю, если
и равное нулю, если 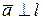 . Правило, сопоставляющее каждому вектору его проекцию на ось, называется операцией проектирования. Обозначение пр
. Правило, сопоставляющее каждому вектору его проекцию на ось, называется операцией проектирования. Обозначение пр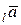 .
.
ТЕОРЕМА 1) пр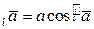 . 2)
. 2) 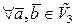 пр
пр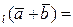 пр
пр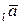 + пр
+ пр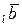 .
.
3) 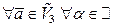 пр
пр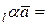

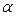 пр
пр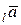 , то есть операция проектирования является линейным функционалом. 4) Фиксируем ПДСК в
, то есть операция проектирования является линейным функционалом. 4) Фиксируем ПДСК в 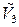 . Тогда проекции вектора на оси
. Тогда проекции вектора на оси
координат 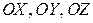 совпадают с компонентами этого вектора в базисе
совпадают с компонентами этого вектора в базисе 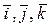 : если
: если 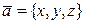 , то
, то 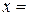 пр
пр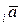 ,
, 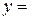 пр
пр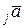 ,
, 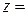 пр
пр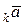 ;
;
5) Косинусы 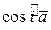 ,
, 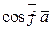 ,
, 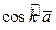 называются направляющими
называются направляющими
косинусами вектора 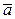 и связаны равенством
и связаны равенством 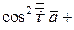
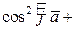
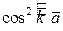 =1.
=1.
СЛЕДСТВИЕ Скалярное произведение векторов связано с операцией проектирования равенством 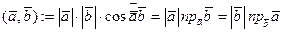 .
.
ЗАМЕЧАНИЕ Пусть точка 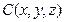 делит отрезок
делит отрезок 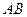 с концами в точках
с концами в точках
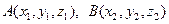 в отношении
в отношении 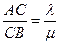 . Тогда координаты
. Тогда координаты 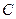 вычисляются по
вычисляются по
формулам 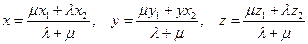 .
.
____
В следующей теореме собраны свойства скалярного произведения.
ТЕОРЕМА 1) 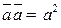 . 2)
. 2) 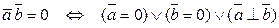 . 3)
. 3) 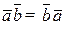 .
.
4) Скалярное произведение является билинейной формой на 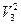 .
.
5) Если в ПДСК 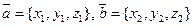 , то
, то 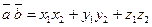 .
.
Определение (физический смысл скалярного произведения) Работой постоянной силы 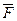 по перемещению материальной точки из начала в конец вектора
по перемещению материальной точки из начала в конец вектора 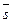 называется величина
называется величина 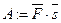 .
.
_____
Определение Упорядоченная тройка некомпланарных векторов 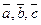 с общим началом называется правой (левой), если из конца вектора
с общим началом называется правой (левой), если из конца вектора 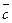 движение от
движение от 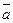 к
к 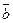 по кратчайшему из двух углов происходит против (по) часовой стрелки(е).
по кратчайшему из двух углов происходит против (по) часовой стрелки(е).
Определение Векторным произведением векторов 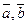 называется вектор
называется вектор 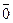 , если
, если 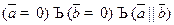 . В противном случае векторным произведением
. В противном случае векторным произведением 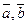 называется вектор
называется вектор 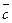 , который вполне определяется свойствами:
, который вполне определяется свойствами:
1) 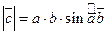 ; 2)
; 2) 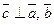 ; 3)
; 3) 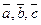 - правая тройка векторов.
- правая тройка векторов.
Определение Смешанным произведением трех векторов 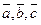 называется число
называется число 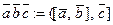 .
.
ЗАМЕЧАНИЕ 1 (геометрический смысл модуля)
1) 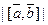 численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах 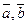 как на сторонах. 2)
как на сторонах. 2) 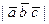 численно равен объему призмы, построенной на векторах
численно равен объему призмы, построенной на векторах 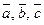 как на ребрах
как на ребрах 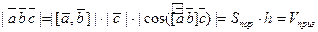 .
.
ЗАМЕЧАНИЕ 2 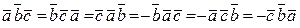 .
.
В следующей теореме собраны свойства векторного произведения.
ТЕОРЕМА 1) Векторное произведение является билинейным отображением из
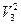 в
в 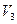 . 2) Если
. 2) Если 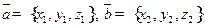 , то
, то 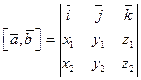 .
.
СЛЕДСТВИЕ Ненулевые векторы 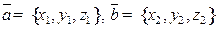 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 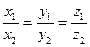 .
.
Векторное произведение имеет до десятка физических смыслов. Приведем наиболее характерные.
Определение (физический смысл векторного произведения). Моментом относительно точки 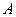 силы
силы 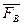 , приложенной к точке
, приложенной к точке 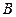 , называется вектор
, называется вектор 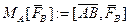 .
.
Определение (физический смысл векторного произведения) Пусть материальная точка  вращается по окружности (с центром
вращается по окружности (с центром 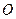 ) с линейной скоростью
) с линейной скоростью 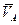 . Вектором угловой скорости вращения этой точки относительно цента
. Вектором угловой скорости вращения этой точки относительно цента 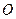 называется расположенный на оси вращения вектор
называется расположенный на оси вращения вектор 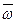 , определяемый равенством
, определяемый равенством 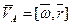 . Это равенство называется формулой Эйлера.
. Это равенство называется формулой Эйлера.
В следующей теореме собраны свойства смешанного произведения.
ТЕОРЕМА 1) 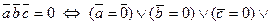 (векторы
(векторы 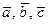 компланарны)
компланарны)
2) Смешанное произведение является 3– линейной формой: 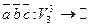 .
.
3) Если 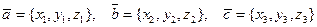 , то
, то 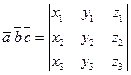 .
.
Напомним, что плоскостью L (2 - плоскостью) в 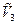 с фиксированной ПДСК называется множество точек, координаты которых удовлетворяют уравнению
с фиксированной ПДСК называется множество точек, координаты которых удовлетворяют уравнению 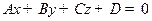 , где
, где 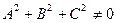 . Определение Вектором нормали к плоскости называется вектор, перпендикуляр ный любому вектору, начало и конец которого лежат в этой плоскости. Определение Углом между плоскостями называется угол между их векторами нормалей. В зависимости от выбранных векторов нормалей этот угол имеет два значения. ТЕОРЕМА Пусть заданы 3 плоскости
. Определение Вектором нормали к плоскости называется вектор, перпендикуляр ный любому вектору, начало и конец которого лежат в этой плоскости. Определение Углом между плоскостями называется угол между их векторами нормалей. В зависимости от выбранных векторов нормалей этот угол имеет два значения. ТЕОРЕМА Пусть заданы 3 плоскости 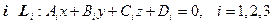 ;
; 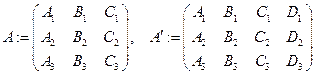 . Тогда имеют место следующие утверждения. 1)
. Тогда имеют место следующие утверждения. 1) 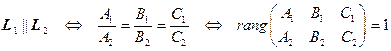 . 2)
. 2)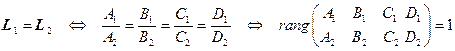 . 3) Плоскости
. 3) Плоскости 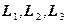 пересекаются в одной точке тогда и только тогда, когда
пересекаются в одной точке тогда и только тогда, когда 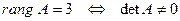 .
.
4) плоскости 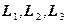 пересекаются по одной прямой тогда и только тогда, когда
пересекаются по одной прямой тогда и только тогда, когда 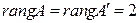 . 5)
. 5) 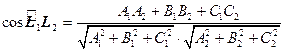 . 6) Расстояние от точки
. 6) Расстояние от точки 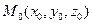 до плоскости
до плоскости 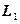 вычисляется по формуле
вычисляется по формуле
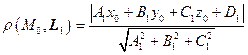 .
.
Определение Пусть векторы 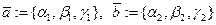 не коллинеарны, и задана точка
не коллинеарны, и задана точка 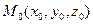 . Формула
. Формула 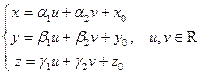 , определяющая множество точек с координатами
, определяющая множество точек с координатами 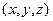 в
в 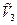 , называется параметрическим уравнением плоскости. ЗАМЕЧАНИЕ а) Если плоскость задана параметрическим уравнением, то ее общее уравнение имеет вид
, называется параметрическим уравнением плоскости. ЗАМЕЧАНИЕ а) Если плоскость задана параметрическим уравнением, то ее общее уравнение имеет вид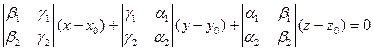 . б) Если плоскость задана уравнением
. б) Если плоскость задана уравнением 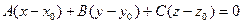 и для определенности
и для определенности 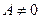 , то ее параметрическое уравнение можно задать, например, в виде
, то ее параметрическое уравнение можно задать, например, в виде 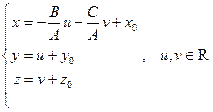 . Следующее замечание доказывается аналогично теореме.
. Следующее замечание доказывается аналогично теореме.
ЗАМЕЧАНИЕ Пусть в какой-либо ПДСК в евклидовой плоскости 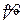 заданы две прямые
заданы две прямые 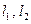 уравнениями
уравнениями 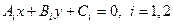 . Тогда справедливы следующие утверждения. 1)
. Тогда справедливы следующие утверждения. 1) 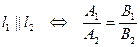 . 2)
. 2) 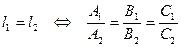 . 3)_
. 3)_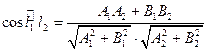 . 4) Расстояние от точки
. 4) Расстояние от точки 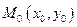 до прямой
до прямой 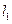 вычисляется по формуле
вычисляется по формуле 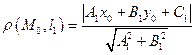 .
.
_____
Определение Множество точек, координаты которых 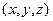 удовлетворяют СЛАУ
удовлетворяют СЛАУ 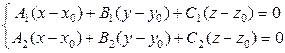 , (1) где
, (1) где 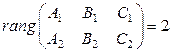 , называется уравнением прямой в
, называется уравнением прямой в 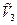 , проходящей через точку
, проходящей через точку 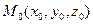 . Определение Пусть даны вектор
. Определение Пусть даны вектор 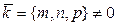 и точка
и точка 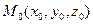 . Система уравнений вида
. Система уравнений вида 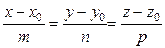 (2)
(2)
называется каноническим уравнением прямой.
Формула, 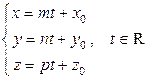 , (3) определяющая множество точек в
, (3) определяющая множество точек в 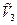 с координатами
с координатами 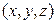 , называется параметрическим уравнением прямой. ЗАМЕЧАНИЕ 1 Направляющий вектор
, называется параметрическим уравнением прямой. ЗАМЕЧАНИЕ 1 Направляющий вектор 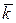 параллелен любому вектору, начало и конец которого лежат на этой прямой. ЗАМЕЧАНИЕ 2 Уравнения (1), (2), (3), в которых
параллелен любому вектору, начало и конец которого лежат на этой прямой. ЗАМЕЧАНИЕ 2 Уравнения (1), (2), (3), в которых 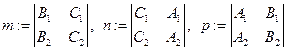 задают одну и ту же прямую в
задают одну и ту же прямую в 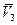 . Определение Углом между двумя прямыми называется угол между направляю щими векторами этих прямых. Этот угол принимает два значения. ТЕОРЕМА Пусть даны две прямые
. Определение Углом между двумя прямыми называется угол между направляю щими векторами этих прямых. Этот угол принимает два значения. ТЕОРЕМА Пусть даны две прямые 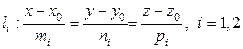 и плоскость
и плоскость 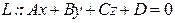 . Тогда имеют место утверждения. 1)
. Тогда имеют место утверждения. 1) 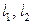 скрещиваются
скрещиваются 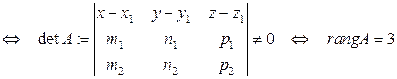 . 2)
. 2) 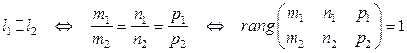 3)
3) 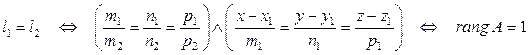 . 4)
. 4) 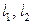 пересекаются
пересекаются 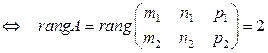 . 5)
. 5) 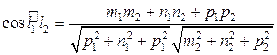 . 6) Расстояние от точки
. 6) Расстояние от точки 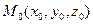 до прямой
до прямой 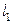 вычисляется по формуле
вычисляется по формуле
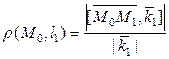 . 7) Расстояние между двумя прямыми вычисляется по формуле
. 7) Расстояние между двумя прямыми вычисляется по формуле 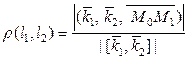 .
.
Приведем без доказательства виды уравнения прямой в евклидовой плоскости 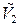 . ЗАМЕЧАНИЕ а)
. ЗАМЕЧАНИЕ а) 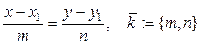 - каноническое уравнение прямой на плоскости. б)
- каноническое уравнение прямой на плоскости. б) 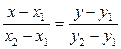 - уравнение прямой, проходящей через две точки
- уравнение прямой, проходящей через две точки 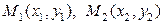 . в)
. в)
 2014-02-09
2014-02-09 1058
1058








