Лекция №3 Непараметрическое (независящее от распределения) обучение дискриминантных функций

3.1. Пространство весов

Мы уже обсуждали тот факт, что вектор образа X представляется как точка в пространстве образов и что пространство может быть разбито на подобласти для образов, принадлежащих различным категориям. Решающая поверхность, которая делит пространство может быть линейной, кусочно-линейной или нелинейной и может быть в общем виде представлена как:

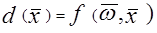
где 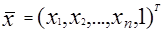и

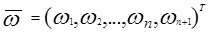
представляют собой образ и весовой вектор. Проблема обучения системы состоит в том, чтобы найти вектор W, показанный на рис.3.1 на основе априорной информации, полученной от обучающей выборки. Возможно и даже более удобно исследовать поведение обучающих алгоритмов в пространстве весов. Пространство весов есть (n+1) - размерности Эвклидова пространства, в котором координаты w₁ w₂... w_n+1. Для каждого прототипа 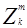, k=1,2,...,M, m=1,2,...,N_k (где M представляет число категорий и N_k представляет собой число прототипов, принадлежащих к категории K, в пространстве W ( пространство весов) имеется гиперплоскость, в которой

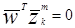
любой весовой вектор W на положительной стороне гиперплоскости дает w^Тz..> 0. Т.е., если прототип 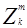принадлежит категории w₁, любой весовой вектор W на этой стороне гиперплоскости будет вероятно классифицировать 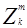. Аналогичные аргументы могут быть рассмотрены для любого весового вектора на другой стороне гиперплоскости, где w^Тz..< 0.

Возьмем 2-х классовую проблему для иллюстрации. Предположим, что мы имеем последовательность N₁ образов, принадлежащих w₁ с общим числом образов N = N₁ + N_l. Предположим также, что w₁ и w₂ -два линейно разделяемых класса. Тогда может быть найден вектор w, такой,что:

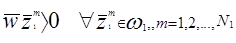
и

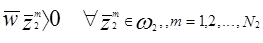
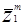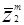где.и представляют собой категории w₁ и w₂ соответственно.

В общем, для N образов имеется N гиперплоскостей в весовом пространстве. Область решения для категории w₁ в W - пространстве это область, которая лежит на положительной стороне N₁ гиперплоскостей для категории w₁ и на отрицательной для N₂ гиперплоскостей для категории w₂. Предположим, что мы имеем три прототипа Z¹, Z², Z³ и знаем, что все они принадлежат категории w₁. Три гиперплоскости могут быть нарисованы в W - пространстве, как показано на Рис.3.1а, заштрихованная область на Рис.3.1а показывает решающие области в двухклассовой проблеме. 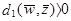В этой област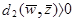и

и

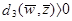
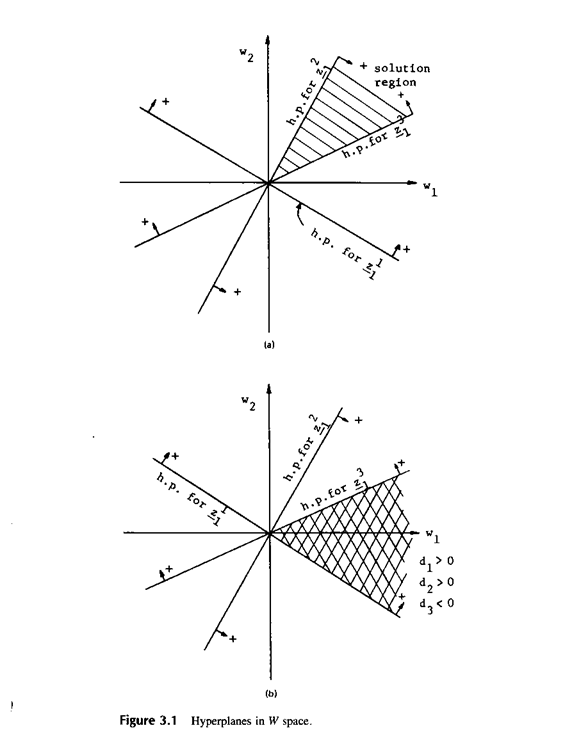
Т.е. любое 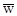в этом районе будет вероятно классифицировать прототипы Z¹, Z², Z³ как принадлежащие w₁, в то время как поперечно заштрихованные области, показанные на рис.3в

d₁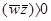

d₂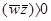

но d₃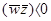® любой w из этой области будет классифицировать Z¹ и Z² как принадлежащий категории w₁ и классифицировать Z³ как относящийся к категории w₂.

Как обсуждалось в части 2 решающая поверхность для двухклассовой задачи предполагает, что d(w,x) будет больше 0 для всех образов из одного класса и меньше 0 для образов, принадлежащих к другому классу. Но если все 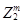заменить на их отрицательные значения - 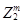, то решающая поверхность может быть обобщена как часть w пространства, в котором:

w^Tzñ0 "₌-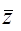

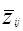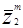
наша проблема становится в нахождении w, которое обеспечивает положительность всех неравенств.

Иногда может быть желательно иметь ограничение (порог) в дискриминантной функции, такой что:

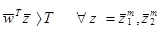, (3.6)

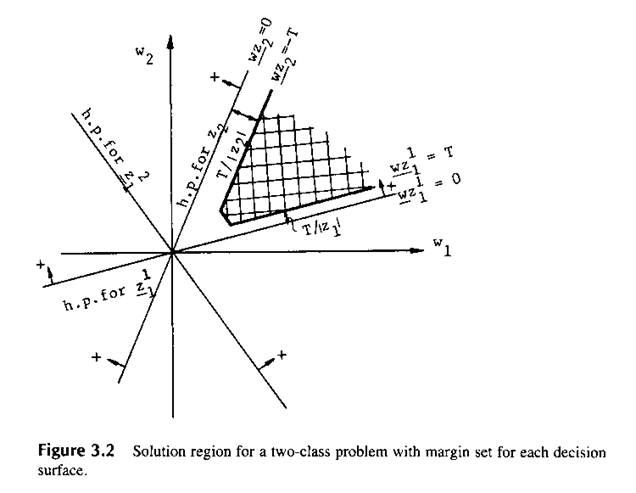
где T>0 ограничение (порог). Любой 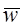, удовлетворяющий неравенству (3.6) является весовым вектором решения. Решающая область теперь изменяется так, как показано на рис.3.2.

В заштрихованной области: оба 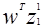и 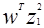- положительные, в то время как 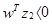отметим, что вдоль исходной гиперплоскости образа

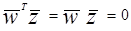, (3.7)

и что вектор Z (расширенный Z) является перпендикулярным к гиперплоскости 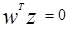и направлен в ее положительную сторону. Тогда линия 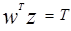отстоит от 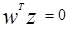на расстояние 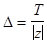. Доказательство этого оставим читателю.

3.2. Процедура обучения с коррекцией ошибок

Очевидно, что для случая двух классов ошибка может существовать, если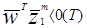

.

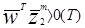Тогда нам необходимо подвинуть весовой вектор в положительную сторону гиперплоскости для 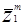, другими словами передвигаем вектор W в область правильного решения. Наиболее прямой путь сделать это - передвинуть W в направлении перпендикулярном к гиперплоскости (т.е. в направлении от 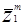или -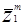). Вообще коррекция W может быть сформулирована следующим образом:

заменить W(k) на W(k+1), так что

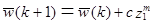, если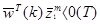

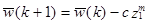, если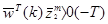

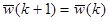, если классифицировано правильно,

где 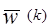и 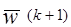- весовые вектора на k-ом и (k+1)-ом шагу коррекции, соответственно. Добавление корректирующего члена 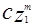заставляет вектор 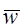двигаться в направлении 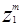. Аналогично, вычитание корректирующего члена передвигает вектор 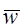направлении -.

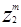В течение этой обучающей процедуры образы представляются по одному, всего N=N₁ + N₂ прототипов (обучающих образов). После одной итерации все образы представляются снова в той же последовательности, чтобы получить новую итерацию.

Существует несколько правил выбора величины С:

- правило с фиксированной коррекцией,

- правило абсолютной коррекции,

- правило частичной коррекции.

3.2.1. Правило с фиксированной коррекцией

В этом алгоритме С - выбирается как фиксированная положительная константа. Этот алгоритм начинается с любого w(0) и выражение (3.10) применяется к обучающей последовательности P, P = .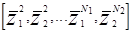

В целом процесс настройки весов будет закончен за конечное число шагов. Выбор С для этого процесса не очень важен. Если теорема сходимости справедлива для С=1, то она будет справедлива для любого С ¹1, так как изменение С фактически масштабирует все образы без изменения их разделимости.

3.2.2. Правило абсолютной коррекции

В этом алгоритме Свыбирается как наименьшее целое число, которое передвигает 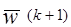поперек гиперплоскости образа в область решения w каждый раз как классификатор делает ошибку. Пусть 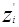- среднее из векторов, которые не удовлетворяют неравенству w ´ z ³T. Константа С выбирается так, что

,

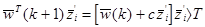
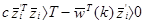поэтому

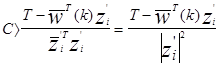
Если Т=0, 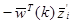должно быть больше 0 или 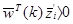. Взяв абсолютную величину в (3.3) получаем

.

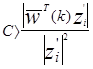Правило абсолютной коррекции также дает решающий весовой вектор за конечное число шагов.

3.2.3. Правило с частичной коррекцией

В W пространстве расширенный вектор образа Z - перпендикулярен гиперплоскости 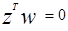и направлен в положительном направлении, как показано на рис.3.3.

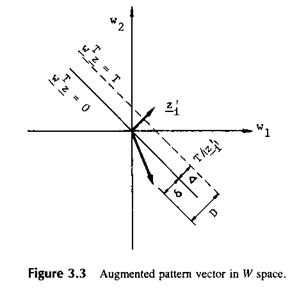Расстояние от 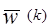до желаемой гиперплоскости будет:

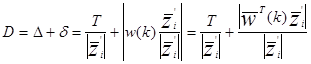(3.15)

Когда 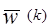находится на другой стороне гиперплоскости

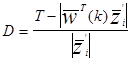
В алгоритме с частичной коррекцией С - выбрано так, что 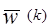двигается на часть расстояния в направлении нормали к желаемой гиперплоскости. То есть

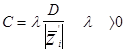
и

-=

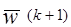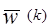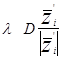
Если порог положить равным 0, то:

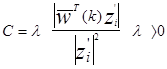
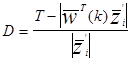
можно видеть, что когда l=1 коррекция происходит до гиперплоскости (правило абсолютной коррекции) и когда l<1 коррекция короче, чем до гиперплоскости (under relaxation), когда l>1 коррекция больше чем до гиперплоскости, (over relaxation).

Для 0<l<2 правило частичной коррекции будет или заканчиваться на весовом векторе в конечное число шагов или сходиться к точке на границе решающего пространства весов.

Процедура обучения для всех перечисленных 3-х алгоритмов выглядит следующим образом:

1) Взять любой 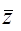из обучающей последовательности и проверить d(z), для определения класса (предполагается М=2).

2) Если получен правильный ответ, переходим к следующему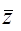

3) Если имеет место ошибочнаяклассификация, изменяем w(k) на w(k+1).

4) После того, как будут проверены все 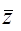из обучающей последовательности, повторяем все процедуры заново в том же порядке. Если 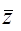линейно разделимы, все три алгоритма будут сходиться к правильному .

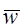На рис 3.4. показаны шаги коррекции для трех различных алогритмов. Абсолютная коррекция заканчивается за 3 шага, в то время как частичная за 4 шага.

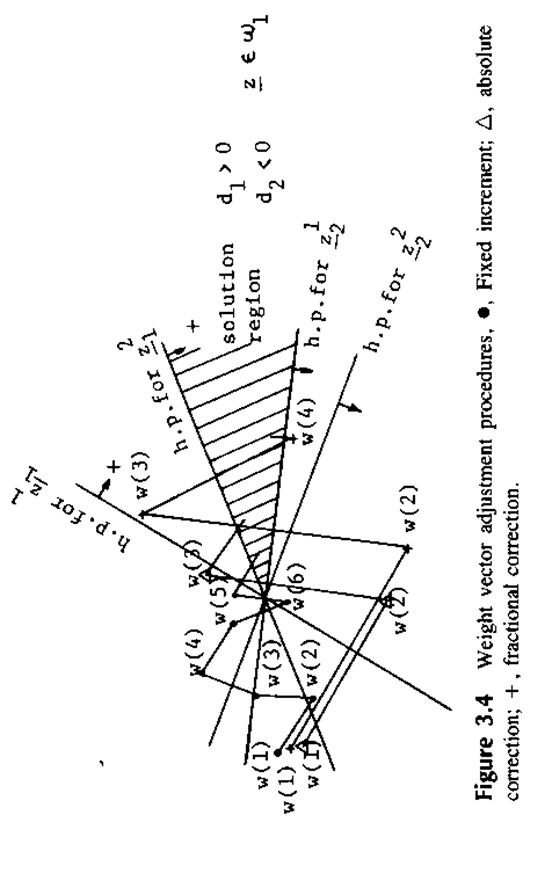
Рис 3.4.

Для количества классов больше 2 (M>2) может быть предложена подобная процедура. Предположим, что мы имеем обучающую последовательность для всех образов классов w_i i=1,2,...,M.

Вычислим дискриминантные функции

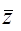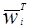
d_i()=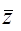, i=1,2,...,M

Очевидно, мы желаем:

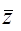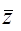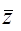d_i()>d_j() Î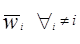

3.3. Градиентные методы

3.3.1. Общий метод градиентного спуска

Метод градиентного спуска является другим приближением к обучающим системам. Градиентный вектор обладает важным свойством указывающий максимальную скорость увеличения функции по мере увеличения аргумента. Процедура настройки весов может быть сформулирована как:

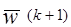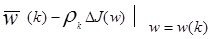= (3.25)

где J(w) - критерий качества, который минимизируется настройкой 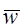. Минимум J(w) может быть достигнут передвижением 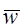в направлении отрицательного градиента. Процедура может быть описана следующим образом:

1. Начать с некоторого произвольно выбранного вектора w(1) и вычислить градиентный вектор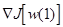

2. Получаем следующую величину w(2) передвигаясь на некоторое расстояние от w(1) в направлении наиболее крутого спуска.

r_k в уравнении (3.25) - положительный скалярный множитель, который устанавливает размер шага. Для его оптимального выбора предполагаем, что J(w) может быть аппоксимирован как:

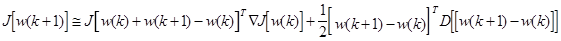(3.26)

где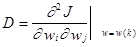

подставляя (3.25) в (3.26) получим:

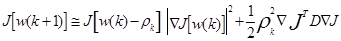(3.27)

Полагая

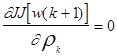для минимизации 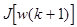мы получим

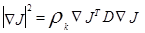(3.28)

или

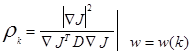, (3.29)

которое эквивалентно алгоритму Ньютона для оптимального спуска, в котором

r_k = D ^-1.

Некоторые проблемы могут возникнуть с этим оптимальным r_k; D ^-1 в (3.29) может не существовать; используемые матричные операции требуют значительных временных затрат; предположение поверхности второго порядка может быть некорректным. Исходя из этих соображений лучшим выходом будет положить r_k равным константе.

3.3.2. Персептронная функция критерия

Пусть функция критерия будет:

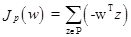(3.31)

где суммирование осуществляется по неправильно классифицированным векторам образов. Геометрически J_p(w) пропорционально сумме расстояний неправильно классифицированных образов от гиперплоскости.

Возьмем производную от J_p(w) по w(k):

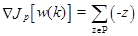(3.32)

где w(k) означает величину w на k-ой итерации. Персептронный обучающий алгоритм может быть сформулирован как

w(k+1) = w(k) - 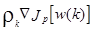(3.33)

w(k+1) = w(k) + 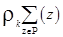(3.34)

где Р - последовательность неправильно классифицированных образов при данном w(k). Уравнение (3.34) может быть затем интерпретировано в том смысле, что (k+1) весовой вектор может быть получен добавлением умноженной на некоторый множитель сумму неправильно классифицированных образов для

k-ого весового вектора.

Это процедура, называемая "many-at-time" ("большое время"), т.к. мы определяем w^Tz для всех zÎР, только после того как все образы были классифицированы.

Если мы делаем настройку после каждого неправильно классифицированного образа (мы называем это "one-at-a-time") процедура функция критерия становится

J(w) = -w^Tz (3.35)

и

ÑJ(w) = -z

Алгоритм обучения будет иметь вид

w(k+1) = w(k) +r_kz (3.37)

Это правило с фиксированным инкрементом, если r_k = с (константа).

3.3.3. Релаксационная функция критерия

Функкция критерия, используемая в этом алгоритме, имеет вид

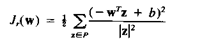(3.38)

Р - здесь снова последовательность неправильно классифицированных образов при заданном w. То есть Р состоит из тех z, для которых -w^Tz +b>0

или: w^Tz < b. Градиент J_r(w) по w(k) дает

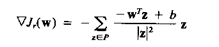(3.39)

Базовый релаксационный обучающий алгоритм формулируется как

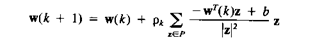(3.40)

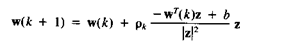Это также "many-at-time" алгоритм. Соответствующий "one-at-a-time" алгоритм будет:

(3.41)

который становится алгоритмом частичной коррекции с l = r_k.

3.4. Обучение кусочно-линейных машин

В общем случае не существует теорем сходимости для для обучающих процедур коммитет или других кусочно-линейных машин. Одна процедура, которая часто бывает удовлетворительной приводится ниже. Пусть М=2 и имеется R дискриминантных функций, где R - нечетное. Тогда

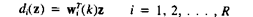(3.42)

Классификация в коммитет-машине будет затем выполняться согласно

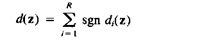(3.43)

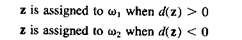так что

(3.44)

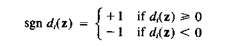где:

(3.45)

Отметим, что так как R - нечетное, d(z) не может быть равно 0 и будет всегда нечетным. Так как d(z) равно разнице между числом d_i(z) >0 и d_i(z) < 0 для весового вектора w_i (k) для k-ой итерации. В нашем случае мы всегда желаем иметь d_i(z) >0. Другими словами мы желаем иметь больше весовых векторов, которые дают d_i(z) >0.

Когда d_i(z) < 0, имеет место неправильная классификация. Будет очевидным, что в этом случае будет [ R+d(z) ] / 2 весовых векторов среди w_i (k), i=1,2,...,R, которые дают отрицательные ответы [d_i(z) < 0] и [ R-d(z) ] / 2 весовых векторов, которые дают положительные ответы [d_i(z) >0]. Для получения правильной классификации нам необходимо изменить, по крайней мере n ответов w_i (k) от -1 к +1, где n может быть найдено из уравнения:

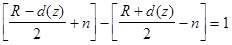(3.46)

В первых скобках представлено число d_i, которое сейчас больше нуля, выражение в скобках после минуса представляет число d_i, которое меньше нуля. Минимальная величина n тогда будет

n_min = [d(z) + 1] / 2, (3.47)

которое дает минимальное число векторов, необходимых для настройки.

Процедура для настройки весового вектора:

1) убираем наименьший отрицательный d_i(z) среди отрицательных d_i(z);

2) настраиваем [d(z) + 1] / 2 весовых векторов по следующему правилу:

w_i (k+1) = w_i (k) + сz, (3.48)

таким образом, что из результирующие d_i(z) становятся положительными. Все другие весовые векторы остаются неизменными на этой стадии;

3) если на k-ой стадии машина неправильно классифицирует образ, принадлежащий w₂, делаем классифицирующие коэффициенты с отрицательной величиной, так что

w_i (k+1) = w_i (k) - сz.

3.5. Практические соображения, касающиеся метода обучения

с коррекцией ошибок.