Кусочно-линейные дискриминантные функции (КЛД)
Классификация по минимуму расстояния
Хотя этот классификатор был предложен достаточно давно, до сих пор он остается эффективным инструментом решения задачи классификации.
Решающее правило, используемое в этом методе, имеет вид:
x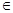 Wj , если D(x, zj)=
Wj , если D(x, zj)=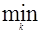 D(x, zk), k=1,…M
D(x, zk), k=1,…M
где D(°) — метрика, называемая евклидовым расстоянием образа х от zk, и zk — есть эталонное среднее (или центр класса) для класса Wk.
Тогда
D(x, zk) = |x - zk|
Исходя из D(x, zk) > D(x, zj) 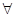 j,k
j,k
Имеем
D2(x, zk) > D2(x, zj)
Другими словами, мы можем использовать D2 вместо D в решающем правиле:
D2(x, zk) = |x - zk|2
Или в матричной форме
D2(x, zk) = (x - zk)т (x - zk) = хтх –2хт zk + zkт zk
Учитывая, что выражение хтх является постоянной для всех к, его можно отбросить. Тогда поиск минимума D(x, zk) эквивалентен поиску
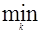 [–2хт zk + zkт zk]
[–2хт zk + zkт zk]
или альтернативно мы должны найти
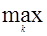 [хт zk - ½zkт zk], к=1,2,…М
[хт zk - ½zkт zk], к=1,2,…М
Последнее выражение определяет классификатор по минимуму расстояния. ДФ, используемая в классификаторе, может быть выражена как
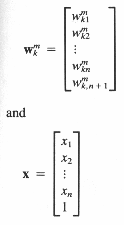
dk(Х) = хт zk - ½zkт zk = хт zk - ½ |zk|2 = хт W
где
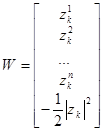
и 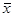 — расширенный вектор
— расширенный вектор
Отметим, что решающая поверхность между любыми двумя классами Wi и Wj образуется плоскостью, перпендикулярной линии zi - zj, проходящей через ее середину.
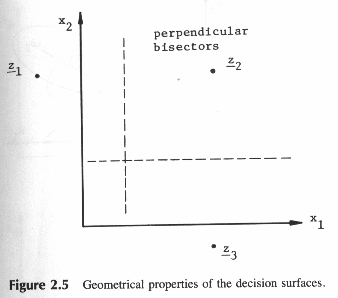
Рис.
Доказательство этого очень просто.
Уравнение решающей поверхности классами W1 и W2 имеет вид
d(Х) = хт (z1 – z2 ) - ½(z1т z1 – z 2т z2 =0
Возьмем точку — середину отрезка, соединяющего z1 , z2
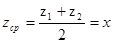
Подставим zср в выражение d(x)
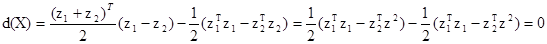
Очевидно, сама гиперплоскость, разделяющая W1 и W2 определяется вектором нормали:
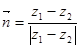
Отметим, что классификатор по минимуму расстояния использует для представления каждого класса одну точку.
Такое представление будет справедливым для случая нормального распределения с равными дисперсиями по каждой координате, как показано на рис.2.6а
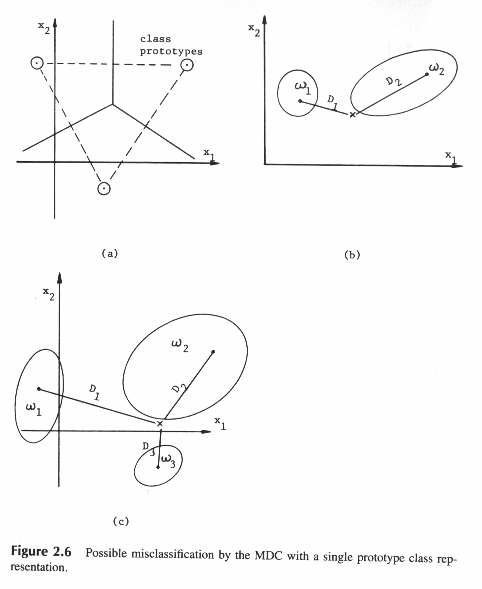
рис.2.6
Однако в случае, если классы не будут нормально распределенными с одинаковыми дисперсиями по всем координатам, как показано на рис.2.6.b, то будет иметь место неправильная классификация.
Даже если D1 < D2, точка + должна быть отнесена к W2 вместо W1. Аналогично, на рис.2.6с точка + должна быть отнесена к W3 по минимуму расстояния, однако она ближе кW2.
Т.о., представление класса одной точкой не является хорошим решением. Если представить каждую категорию образов с помощью мультипрототипов, вместо единичного прототипа, тогда
D(x, Wk)=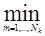 [ D(x, zkm)], (2.21)
[ D(x, zkm)], (2.21)
Где к представляет к-ую категорию, m — номер m-го прототипа, Nк — число прототипов для категории к.
Это уравнение дает наименьшее расстояние между Х и каждым прототипом из Wk.
Тогда решающее правило становится таким
x 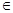 Wj, если D(x, Wj)=
Wj, если D(x, Wj)=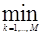 [ D(x, Wk)],
[ D(x, Wk)],
где D(x, Wk) дается выражением (2.21)
ДФ изменяется соответственно так
dk(Х) = 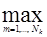 [хт zkm - ½|zkm|2], к=1,2,…М
[хт zkm - ½|zkm|2], к=1,2,…М
2.2.3. Линейная разделимость
Говорят, что классы линейно разделимы, если они классифицируются какой-либо линейной функцией, как,например, показано на рис.2.7а
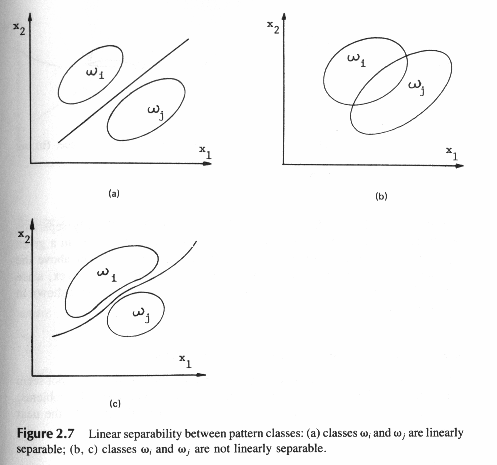
рис.2.7 Линейная разделимость между классами
(а) классы Wi иWj линейно разделимы
(b) (c) классы Wi иWj не разделимы линейно
Из рис.2.7 видно, что решающая поверхность в линейно-разделимом случае является выпуклой. По определению говорят, что функция выпуклая в данной области, если прямая линия, проведенная в данной области, лежит целиком в или выше функции.
Пример выпуклой функции (рис.2.8а)
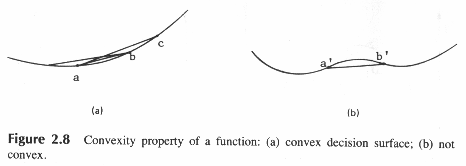
рис.2.8 Свойство выпуклости функции
(а) выпуклая решающая функция
(b) невыпуклая решающая функция
КЛД позволяют решить эффективно проблемы классификации для линейно неразделимого случая.
Кусочно-линейная функция — это функция, которая линейна в отдельных областях пространства признаков. КЛДФ дают кусочно-линейные границы между классами (категориями) как показано на рис.2.9а.

рис.2.9. Кусочно-линейная разделимость для различных классов.
Где разделяющая поверхность, показанная на рис. 2.9 невыпуклая.
ДФ определяется как

она состоит в том, что мы находим максимум dkm(x) среди прототипов класса к, где Nk – число прототипов в классе к и
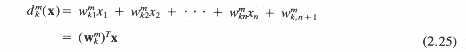
Три различных случая классификации образов могут быть перечислены.
Случай 1.
Каждый класс образов отделяется от других классов одной решающей поверхностью, как показано на рис. 2.10а
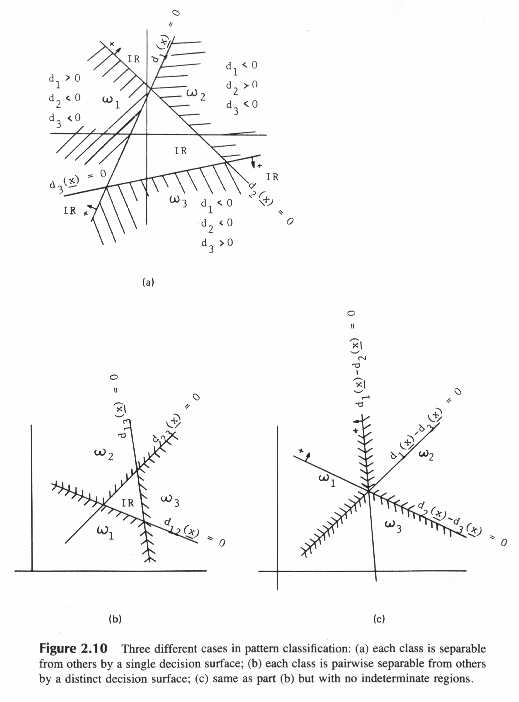
рис.2.10.Три различных случая в распознавании образов
(а) каждый класс отделяется от другого единственной разделяющей плоскостью
(b) каждый класс разделяется попарно от другого отдельной разделяющей плоскостью
(с)тоже, что и (b), но без областей неопределенностей
Случай 2
Каждый касс отделяется от другого класса попарно разделяющей решающей поверхностью. Области неопределенности также могут существовать. В этом случае нет класса, отделяемого от другого одной решающей поверхностью от других.
Например: w1 может быть отделена от w2 поверхностью d12(x)=0 и от w3 d13(x)=0 (рис.2.10.). Всего существует M(M-2)/2 решающих поверхностей, представляемых как dij(x)=0 и 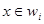 когда dij(x)>0
когда dij(x)>0 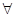 i=j.
i=j.
Случай 3.
Каждый класс отделяется попарно от других классов, но отсутствуют области неопределенности (это специальный вариант случая 2 рис.2.10с). В этом случае имеется М решающих функций.
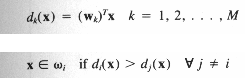
2.3.2. Многослойные машины
Двухслойная машина хорошо известна как коммитет, называется так потому, что в ней есть возможность голосования для каждой ЛДФ, определяющей свою классификацию (р.31).
На рис.2.11. показана такая машина.
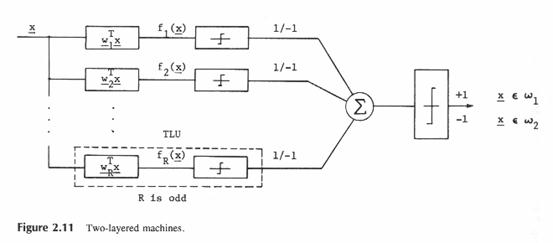
Первый слой_это часть до Σ и справа от него второй слой.
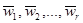 определяют r-различных ДФ, представляют собой n-мерные вектора.
определяют r-различных ДФ, представляют собой n-мерные вектора.

Первый слой состоит из нечеткого числа ДФ, чьи выходы клишируются пороговым логическим элементом как +1 или-1, в зависимости от значения f(x). Второй слой — это одна линейная поверхность с единичным весовым вектором, используемым для решения к какому классу окончательно относится вектор. Когда используется адаптивная обратная связь для обучения порогового логического элемента с 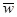 , пороговый логический элемент называется адаптивным пороговым элементом (ADALINE). Когда в машине используется много пороговых элементов, это называется MADALINE — коммитет-машина (commitet).
, пороговый логический элемент называется адаптивным пороговым элементом (ADALINE). Когда в машине используется много пороговых элементов, это называется MADALINE — коммитет-машина (commitet).
Рассмотрим простую двухклассовую проблему для геометрической интерпретации такой машины.
Пусть мы имеем три логических элемента в первом слое:R=3 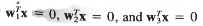 будут определять три гиперплоскости в пространстве признаков, как показано на рис.2.12.
будут определять три гиперплоскости в пространстве признаков, как показано на рис.2.12.
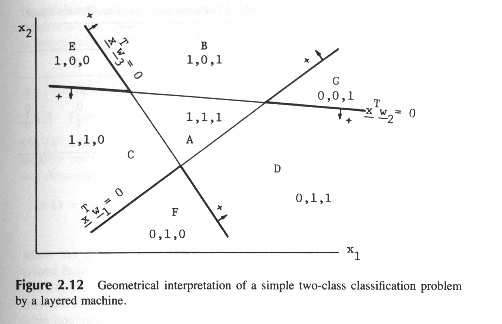
Многослойная машина будет разделять пространство образов геометрически на семь областей. Таблица 2.1 содержит значения 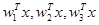 для каждой области с 1 и 0 соответствующих больше или меньше 0, соответственно. Нет областей, которые лежат одновременно на отрицательной стороне всех трех гиперплоскостей так что 0,0,0 никогда не может иметь место.
для каждой области с 1 и 0 соответствующих больше или меньше 0, соответственно. Нет областей, которые лежат одновременно на отрицательной стороне всех трех гиперплоскостей так что 0,0,0 никогда не может иметь место.
Таблица 2.1.
Величины 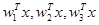 в различных областях пространства образов.
в различных областях пространства образов.

 2014-02-10
2014-02-10 651
651








