Итерационные методы

Сложные неэволюционные задачи и их разностные схемы Ay = - f обычно решаются итерационными методами. Разберем один из таких методов на примере двумерного уравнения (43). Простейшим таким методом является метод Якоби, относящийся к семейству методов последовательных приближений. Процедуру решения с помощью этого метода можно представить в следующем виде:

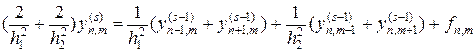, (57)

где s — номер итерации. Уравнение (57) перепишем в форме

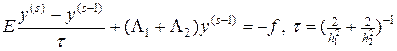. (58)

Метод Якоби и большинство других итерационных методом можно представить в следующей форме:

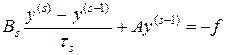. (59)

Когда B и t в (59) не зависят от s, итерационный процесс называют стационарным. Итерационный процесс (59) можно рассматривать как разностную схему некоторой эволюционной задачи. Физический смысл построенной эволюционной задачи не имеет смысла, важно лиши то, чтобы счет на установление состоялся. Несущественно то, что именно аппроксимирует оператор B, существенно лишь то, чтобы 1) он обеспечивал максимально быстрое затухание начальных данных и 2) легко обращался за малое число операций. Продольно-поперечная и локально-одномерная схемы, рассмотренные с точки зрения того, что они являются итерационными процессами, удовлетворяют двум перечисленным выше условиям.

Протестируем итерационную схему Якоби (57) на примере численного решения уравнения

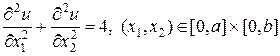, (60)

которое, как нетрудно проверить, при соответствующем подборе граничных условий имеет аналитическое решение

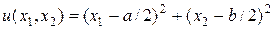. (61)

На листинге_№8 приведен код программы численного решения уравнения (60) итерационным методом Якоби согласно схеме (57).

Листинг_№8

%Программа численного решения двумерного

%эллиптического уравнения (60) итерационным

%методом Якоби по схеме (57)

clear all

%Задаем максимальное число итераций

itermax=300;

%Определяем габариты области по направлениям

%x1 и x2

a=1; b=1;

%Определяем число узлов сетки по координатам

%x1 и x2, а также шаги сетки h1 и h2 и

%вспомогательные величины r1, r2, r3

N=51; M=51;

h1=a/(N-1); h2=b/(M-1);

r1=0.5/(1+(h1/h2)^2);

r2=0.5/(1+(h2/h1)^2);

r3=0.5/(h1^(-2)+h2^(-2));

x1=0:h1:a; x2=0:h2:b;

%Определяем аналитическое решение (61)

for n=1:N

for m=1:M

u(n,m)=(x1(n)-0.5*a)^2+...

(x2(m)-0.5*b)^2;

end

%Определяем начальную итерацию

for n=1:N

for m=1:M

y(1,n,m)=0;

end

%Определяем граничные условия при x2=0 и x2=b

for s=1:itermax

for n=1:N

y(s,n,1)=(x1(n)-0.5*a)^2+...

(x2(1)-0.5*b)^2;

y(s,n,M)=(x1(n)-0.5*a)^2+...

(x2(M)-0.5*b)^2;

end

%Определяем граничные условия при x1=0 и x1=a

for s=1:itermax

for m=1:M

y(s,1,m)=(x1(1)-0.5*a)^2+...

(x2(m)-0.5*b)^2;

y(s,N,m)=(x1(N)-0.5*a)^2+...

(x2(m)-0.5*b)^2;

end

%Определяем ошибку начального приближения, как

%разность численного и аналитического решений

%в норме C

for n=1:N

for m=1:M

z(n,m)=abs(y(1,n,m)-u(n,m));

end

error(1)=max(max(z));

%Организуем цикл основного итерационного

%процесса в методе Якоби

for s=2:itermax

for n=2:(N-1)

for m=2:(M-1)

y(s,n,m)=r1*(y(s-1,n-1,m)+...

y(s-1,n+1,m))+...

r2*(y(s-1,n,m-1)+...

y(s-1,n,m+1))-4*r3;

end

%Определяем ошибку, как разность численного и

%аналитического решений в норме C

for n=1:N

for m=1:M

z(n,m)=abs(y(s,n,m)-u(n,m));

end

error(s)=max(max(z));

end

for n=1:N

for m=1:M

z(n,m)=y(itermax,n,m);

end

%Рисуем численное решение уравнения (60) на

%последней итерации

subplot(1,2,1); surf(x2,x1,z);

%Рисуем кривую зависимости ошибки численного

%решения от номера итерации

subplot(1,2,2); plot(1:itermax,error);

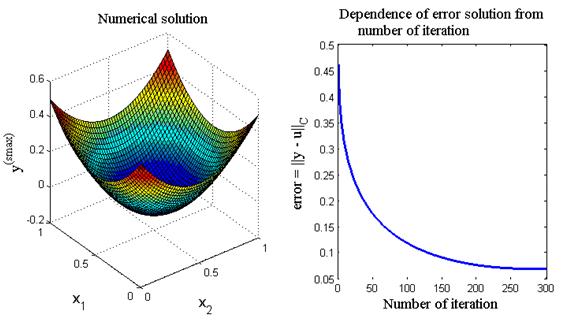
Рис.8. Численное решение задачи (60) методом последовательных приближений
Якоби и кривая зависимости численной ошибки от номера итерации

Код листинга_№8 генерирует итоговый график, вид которого представлен на рис.8. На левом рисунке приведено трехмерное изображение численного решения на последней итерации (s = s _max). Численное решение весьма близко аналитическому решению (61). Справа приведена кривая зависимости ошибки численного решения, рассматриваемой как разность численного и аналитического решений в норме 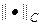, т.е. error = 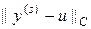, от номера итерации s = 1,…, s _max. Видно, что ошибка по мере увеличения числа итераций уменьшается, но довольно медленно.

Попеременно-треугольную схему рассмотрим на примере численного решения двумерного уравнения вида

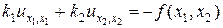. (62)

Для численного решения (62) запишем вспомогательное параболическое уравнение:

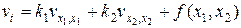. (63)

Для численного решения (63) составим разностную схему, шаблон для которой представлен на рис.9. Разностная схема на рис.9 является полностью неявной, она имеет вид:

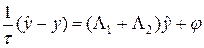. (64)

Разностная схема (64) может быть переписана в канонической форме:

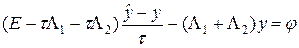. (65)

Схема (65) не является экономичной, поскольку для обращения оператора 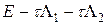требуется, как отмечалось выше, ~ N ⁴ операций в расчете на один узел сетки.

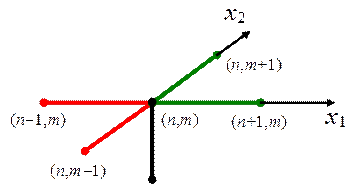
Рис.9. Шаблон разностной схемы (64)

Введем “треугольные” операторы

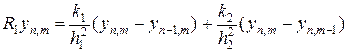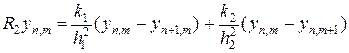определенные на треугольных шаблонах, которые представлены на рис.9 в виде красных и зеленых линий. Очевидно, что L₁ + L₂ = -(R ₁ + R ₂), тогда разностную схему (65) можно переписать в виде:

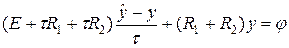. (66)

Немного изменим схему (66), добавив в ее левую часть член 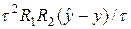, который имеет второй порядок малости O (t ²). Возникнет оператор 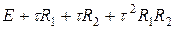, который можно представить в виде произведения 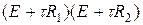, т.е. говорят, что оператор факторизуется. В итоге получается схема, которую называют попеременно-треугольной:

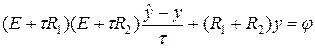. (67)

Операторы E + t R ₁ и E + t R ₁ легко обращаются с помощью процедуры бегущего счета, разобранной в лекции №10 при изучении численного решения уравнений переноса. Алгоритм расчета при процедуре бегущего счета несложен и требует небольшого числа операций в расчете на один узел сетки. Попеременно-треугольная схема переносится на случай любого числа измерений, она может быть обобщена на случай, когда коэффициенты уравнения переменные и даже разрывные, а область интегрирования имеет сложную форму.

Проведем конкретный численный расчет с помощью попеременно-треугольной разностной схемы, решая уравнение (62) с правой частью вида

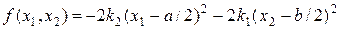. (68)

Нетрудно проверить, что решением задачи (62), (68) в области G = [0, a ]´[0, b ] является выражение:

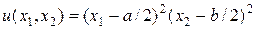. (69)

Перепишем разностную схему (67) в следующем виде:

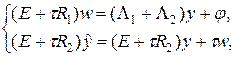(70)

где введено вспомогательное решение w. Распишем систему разностных уравнений более подробно

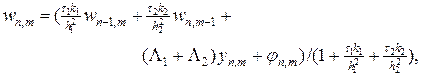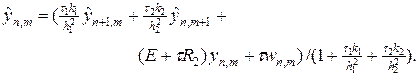(71)

(71¢)

Уравнение (71) решается методом бегущего счета с помощью перехода от точки (x _1,1, x _2,1) к точке (x _1,2, x _2,1) и т.д. к точке (x _1, _N _-₁, x _2,1) и далее после перехода на новый слою по переменной x ₂ от (x _1,1, x _2,1) к (x _1, _N _-₁, x _2,1) и т.д. вплоть до точки (x _1, _N _-₁, x _2, _M _-₁). Движение бегущего счета согласно уравнению (71) состоит в движении слева направо и снизу вверх. Движение счета согласно уравнению (71¢) обратное предыдущему случаю, т.е. от точки (x _1, _N _-₁, x _2, _M _-₁) справа налево и сверху вниз до точки (x _1,1, x _2,1). С учетом аналитического решения (69) в качестве граничных условий задачи (62), (68), принимаем

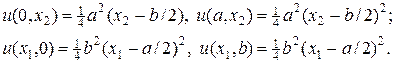(72)

Кроме того, при решении уравнения (71) в качестве граничных условий для переменной w, принимаем

w _0, _m = w_n _,0 = 0, (72¢)

где имеется в виду пространственная сетка x _1, _n = nh ₁, n = 0,1,…, N, x _2, _m = mh ₂, m = 0,1,…, M.

На листинге_№9 приведен код программы, которая численно решает задачу (62), (68), (72) попеременно-треугольным способом по схеме (71), (71¢), (72¢).

Листинг_№9

%Программа численного решения задачи (62),

%(68), (72) попеременно-треугольным способом

function triangle

global a b k1 k2

%Определяем габариты области интегрирования и

%константы k1, k2, входящие в уравнение (62)

a=1; b=1; k1=1; k2=1;

%Определяем число узлов сетки и шаги h1, h2

%по переменным x1, x2

N=35; M=35;

h1=a/(N-1); h2=b/(M-1);

x1=0:h1:a; x2=0:h2:b;

%Определяем шаг в итерационной схеме на

%установление и число шагов на установление

tau=0.001; Nt=30;

r1=(tau*k1)/h1^2; r2=(tau*k2)/h2^2;

r3=1+r1+r2;

%Определяем начальное распределение

for n=1:N

for m=1:M

y(1,n,m)=0.1*randn;

end

%Определяем нижнее и верхнее граничные условия

for t=1:Nt

for n=1:N

y(t,n,1)=u(x1(n),x2(1));

y(t,n,M)=u(x1(n),x2(M));

end

%Определяем левое и правое граничные условия

for t=1:Nt

for m=1:M

y(t,1,m)=u(x1(1),x2(m));

y(t,N,m)=u(x1(N),x2(m));

end

%Оцениваем ошибку отличия численного решения от

%аналитического в норме C

for n=1:N

for m=1:M

z(n,m)=abs(y(1,n,m)-u(x1(n),x2(m)));

end

error(1)=max(max(z));

%Организуем основной цикл итераций на установление

for t=2:Nt

w=zeros(N,M);

%Находим промежуточное решение w согласно (71)

for m=2:(M-1)

for n=2:(N-1)

w(n,m)=(r1*w(n-1,m)+r2*w(n,m-1)+...

(k1/h1^2)*(y(t-1,n-1,m)-...

2*y(t-1,n,m)+y(t-1,n+1,m))+...

(k2/h2^2)*(y(t-1,n,m-1)-...

2*y(t-1,n,m)+y(t-1,n,m+1))+...

f(x1(n),x2(m)))/r3;

end

%Находим решение на следующем слое согласно (71')

for m=(M-1):-1:2

for n=(N-1):-1:2

y(t,n,m)=(r1*y(t,n+1,m)+r2*y(t,n,m+1)+...

y(t-1,n,m)+r1*(y(t-1,n,m)-...

y(t-1,n+1,m))+r2*(y(t-1,n,m)-...

y(t-1,n,m+1))+tau*w(n,m))/r3;

end

%Оцениваем ошибку отличия численного решения от

%аналитического в норме C

for n=1:N

for m=1:M

z(n,m)=abs(y(t,n,m)-u(x1(n),x2(m)));

end

error(t)=max(max(z));

end

for n=1:N

for m=1:M

z(n,m)=y(Nt,n,m);

end

%Рисуем профиль численного решения на последнем шаге

%итерации

subplot(1,2,1); surf(x2,x1,z);

%Рисуем профиль ошибки численного решения от номера

%шага итерации

subplot(1,2,2): plot(1:Nt,error);

%Определяем функцию правой части (68)

function y=f(x1,x2)

global a b k1 k2

y=-2*k2*(x1-0.5*a)^2-2*k1*(x2-0.5*b)^2;

%Определяем аналитическое решение (69)

function y=u(x1,x2)

global a b

y=(x1-0.5*a)^2*(x2-0.5*b)^2;

На рис.10 приведен итог работы кода программы листинга_№9. На левом рисунке приведен трехмерный профиль численного решения по схеме (71), (71¢) задачи Дирихле (62), (68), (72) попеременно-треугольным способом. Трехмерный профиль приведен для численного решения полученного на последнем шаге итерационного процесса, это решение весьма близко к аналитическому решению (69) исходной задачи. На правом рисунке приведена зависимость ошибки численного решения от номера шага итерационного процесса, т.е. error = 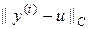, где t = 1,…, t _max — номер итерации.

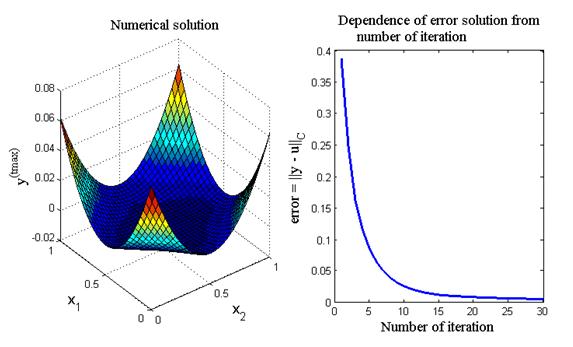
Рис.10. Решение задачи Дирихле (62), (68), (72) попеременно-
треугольным способом

[1] Калиткин Н.Н. Численные методы. — М.: Наука, Глав. ред. физ.-мат. литературы, 1978.

[2] Более подробно о многочленах Чебышева в книге: Калиткин Н.Н. Численные методы. — М.: Наука, Глав. ред. физ.-мат. литературы, 1978 (Приложение, с.501).

[3] Самарский А.А., Гулин А.В. Численные методы. — М.: Наука, Глав. ред. физ.-мат. литературы, 1989, с.317.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: