Счет на установление

Эллиптические уравнения

Лекция №12

Эллиптические уравнения как стационарные решения эволюционных задач. К эллиптическим уравнениям приводит множество физических задач. К ним относятся: определение прогиба нагруженной мембраны, балки и прочие задачи из теории сопротивления материалов, оценка стационарного, т.е. независимого от времени распределения тепла в теле, стационарные течения жидкости, газа в трубах и т.д. Все множество такого рода задач имеет общее свойство, согласно которому считается, что внешние воздействия не зависят от времени, а начальные данные заданы были столь давно, что физическая система успела забыть об этом воздействии и решение стало стационарным и не зависящим от времени, т.е. u = u (r), r = (x ₁,…, x_p).

Примером эллиптического уравнения является задача Дирихле с краевыми условиями первого рода, согласно которой требуется найти непрерывное решение задачи

D u (r) = - f (r), r Î G, u _G(r) = m (r), (1)

где 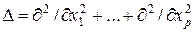, G = G (r) — многомерная замкнутая область с границейG. В отличие от эволюционных уравнений, задача (1) начальные данные не содержит. Обобщением задачи (1) в контексте, например, стационарного уравнения теплопроводности из предыдущей лекции, является уравнение вида:

div[ k (r)grad u (r)] = - f (r), r Î G, u _G(r) = m (r), (2)

где k (r) > 0— коэффициент теплопроводности.

Задачу (2) принято называть стационарной на фоне эволюционного уравнения параболического типа с теми же граничными условиями и с произвольными начальными данными:

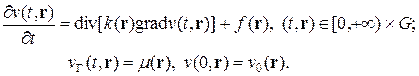(3)

Исследуем вопрос об отличие решения эволюционной задача v (t, r) от решения стационарной задачи u (r). Для этого вычтем уравнение (2) из уравнения (3) и введем обозначение w (t, r) = v (t, r) - u (r), тогда

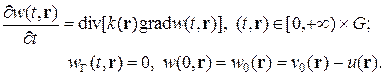(4)

Эволюционная задача (4) имеет однородные (нулевые) краевые условия и произвольные начальные данные, т.к. функция v ₀(r) считалась произвольным начальным распределением.

В курсе математической физики© показано, что решение задачи (4) с помощью метода разделения переменных можно представить в виде следующего бесконечного ряда:

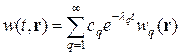, (5)

где l_q, w_q (r) — собственные значения и собственные функции многомерной задачи Штурма-Лиувилля:

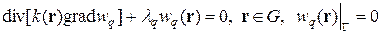. (6)

С учетом (6) коэффициенты c_q, входящие в (5), можно назвать коэффициентами Фурье начальных данных задачи (4) по системе собственных функций w_q (r), т.е.

.

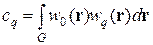Собственные значения l_q задачи (6) положительны и образуют неубывающую последовательность

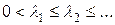, (7)

а собственные функции w_q (r) образуют полную ортонормированную систему в G (r).

Согласно (5), (7), можно получить следующую оценку для нормы решения w (t, r) уравнения (4):

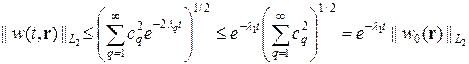. (8)

Неравенство (8) означает, что разность экспоненциально в норме 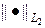при t ® ¥. Другими словами, решение v (t, r) эволюционной задачи (3) среднеквадратично сходится к решению u (r) стационарной задачи (2) при t ® ¥.

Из изложенного выше следует, что вместо задачи (2) для эллиптического уравнения можно взять эволюционную задачу (3) для параболического уравнения с аналогичным пространственным оператором, произвольно выбрать начальные данные и вычислить решение v (t, r) при достаточно большом значении времени t. Стационарный предел u (r), к которому стремится v (t, r) при t ® ¥ является решением стационарной задачи (2).

Такой способ решения эллиптического уравнения называется счетом на установление. Этот способ позволяет использовать для решения эллиптических задач хорошо апробированные схемы решения параболических уравнений, например, продольно-поперечную схему для двумерной задачи и локально-одномерную — для многомерных задач.

Поскольку сходимость к стационарному решению экспоненциальная, т.е. довольно быстрая, постольку, задавая точность e, можно дать следующую оценку для момента достижения нужной точности в счете на установление:

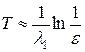, (9)

где l ₁ — наименьшее собственное значение соответствующей задачи Штурма-Лиувилля (6).

Протестируем процедуру счета на установление на примере численного решения двумерного эллиптического уравнения с однородными граничными условиями в прямоугольной области. Запишем соответствующую задачу в следующем виде:

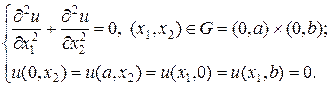(10)

Задача (10) имеет очевидное решение u (x ₁, x ₂) = 0. Построим соответствующую эволюционную задачу:

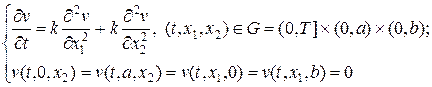(11)

добавим к ней произвольные начальные данные:

v (0, x ₁, x ₂) = v ₀(x ₁, x ₂). (12)

Методом разделения переменных легко решить соответствующую уравнению (11) задачу Штурма-Лиувилля. Получаются следующие собственные значения и собственные функции:

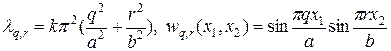, (13)

где q, r = 1,2,… Из (13) легко найти минимальное собственное значение: 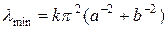, которое позволяет оценить время счета на установление

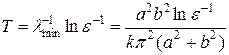(14)

с заданной точностью e.

Задачу (11) решим численно с помощью продольно-поперечной схемы (11.39), (11.39¢) на временном отрезке [0, T ]. Зададимся для определенности точностью e = 10^-8 и рассмотрим соответствующий код программы, представленный на листинге_№1.

Листинг_№1

%Программа решения двухмерного уравнения

%теплопроводности (11) с помощью продольно-

%поперечной схемы

function heat_dim2

global a b vc0 r0 r1

%Определяем габариты области интегрирования

%по времени, направлениям x1 и x2, а также

%коэффициент теплопроводности и константу vc0,

%задающую амплитуду начального распределения

a=1; b=1; koef=0.5; vc0=100;

r0=0.2*min(a,b); r1=0.4*min(a,b);

%Задаем точность расчета eps и время счета T

eps=1e-8;

T=(a^2*b^2*log(1.0/eps))/(koef*pi^2*(a^2+b^2));

%Определяем число шагов по направлениям x1 и x2

N=51; M=51; h1=a/(N-1); h2=b/(M-1);

%Определяем сетки по x1 и x2

x1=0:h1:a; x2=0:h2:b;

%Рисуем начальное распределение в виде

%кольцевой области

for n=1:N

for m=1:M

z(n,m)=v0(x1(n),x2(m));

end

end

subplot(1,2,1); surf(x2,x1,z);

k=0;

%Формируем цикл расчетов с различными шагами по времени

for Nt=100:10:300

tau=T/(Nt-1);

%Определяем начальные данные в виде кольца

for n=1:N

for m=1:M

y(1,n,m)=v0(x1(n),x2(m));

end

end

%Определяем граничные условия при x1=0 и x1=a

for t=1:Nt

for m=1:M

y(t,1,m)=0; y(t,N,m)=0;

end

end

%Определяем граничные условия при x2=0 и x2=b

for t=1:Nt

for n=1:N

y(t,n,1)=0; y(t,n,M)=0;

end

end

%Организуем основной цикл интегрирования по времени

for t=1:(Nt-1)

p1=(0.5*tau*koef)/h1^2;

p2=(0.5*tau*koef)/h2^2;

%Находим решение на полуцелом временном слое,

%т.е. решаем уравнение (11.39)

for m=2:(M-1)

%Учитываем нулевое граничное при x1=0

alpha(2)=0; beta(2)=y(t,1,m);

for n=2:(N-1)

alpha(n+1)=p1/(1+p1*(2-alpha(n)));

beta(n+1)=(y(t,n,m)+p2*(y(t,n,m-1)-...

2*y(t,n,m)+y(t,n,m+1))+p1*beta(n))/...

(1+p1*(2-alpha(n)));

end

%Учитываем нулевое граничное при x1=a

ys(N,m)=y(t,N,m);

for n=N:-1:2

ys(n-1,m)=alpha(n)*ys(n,m)+beta(n);

end

end

%Находим решение на следующем временном слое,

%т.е. решаем уравнение (11.39')

for n=2:(N-1)

%Учитываем нулевое граничное при x2=0

alpha(2)=0; beta(2)=y(t,n,1);

for m=2:(M-1)

alpha(m+1)=p2/(1+p2*(2-alpha(m)));

beta(m+1)=(ys(n,m)+p1*(ys(n-1,m)-...

2*ys(n,m)+ys(n+1,m))+p2*beta(m))/...

(1+p2*(2-alpha(m)));

end

for m=M:-1:2

y(t+1,n,m-1)=alpha(m)*y(t+1,n,m)+beta(m);

end

end

end

%Находим норму решения эволюционной задачи в L2

s=0;

for n=1:N

for m=1:M

s=s+h1*h2*y(Nt,n,m)^2;

end

end

k=k+1;

w(k)=sqrt(s);

tt(k)=tau;

end

%Рисуем зависимость нормы решения ||y(Nt,n,m)||

%в L2 от tau

subplot(1,2,2); semilogy(tt,w);

%Определяем функцию начального распределения

function y=v0(x1,x2)

global a b vc0 r0 r1

r=sqrt((x1-0.5*a)^2+(x2-0.5*b)^2);

y=0;

if (r>=r0)&(r<=r1)

y=vc0*(r1-r)*(r-r0);

end

После работы кода программы листинга_№1 должен появиться график, примерный вид которого представлен на рис.1. Левый рисунок изображает трехмерный профиль начального распределения (12) задачи (11). Это распределение взято в несколько экзотической форме кольца. На правом рисунке приведен график зависимости нормы решения 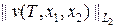в точке t = T в зависимости от шага t по времени продольно-поперечной разностной схемы. Красная пунктирная линия на графике обозначает выбранный уровень точности e = 10^-8. Отчетливо видно, что, начиная с некоторого порогового значения шага сетки t, при всех меньших значениях шага достигается заданный уровень точности сходимости решения эволюционной задачи (11) к решению эллиптической задачи (10).

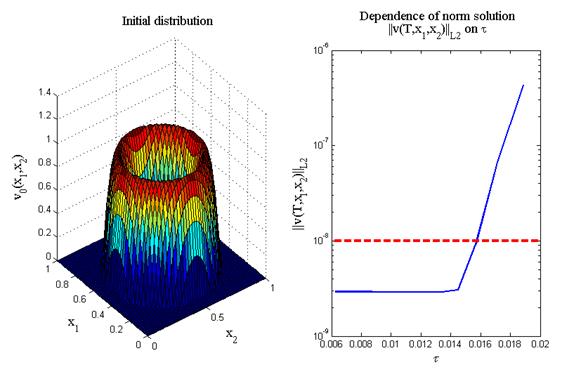
Рис.1. Счет на установление эволюционной задачи (11) вплоть до
выхода на решение эллиптической задачи (10)

Выбор оптимального шага по времени. Из изложенной в предыдущем пункте процедуры счета на установление, следует важность выбора оптимального значения шага по времени между крайностями высокоточной аппроксимации и минимумом количества операций. Для исследования вопроса о величине оптимального шага по времени ограничимся рассмотрением двумерной задачи Дирихле в прямоугольнике:

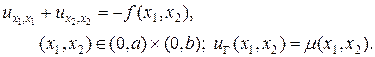(15)

Задаче (15) соответствует эволюционная задача вида:

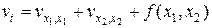, (16)

которую будем решать численно на равномерной сетке 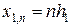, , 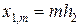n = 0,1,…, N, m = 0,1,…, M, где h ₁ = a / N, h ₂ = b / M.

Для решения задачи (16) рассмотрим продольно-поперечную схему в форме:

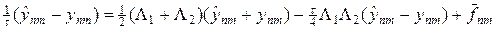
и преобразуем ее в каноническую форму

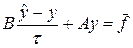, (17)

где

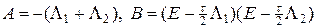, (17¢)

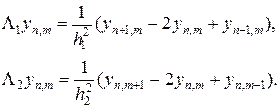(17¢¢)

В процессе численного решения уравнения (16) по схеме (17) при выходе на стационарное решение 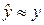. В этом случае в пределе схема (17) переходит в неэволюционную разностную схему вида:

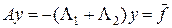, (18)

которая, как нетрудно проверить, аппроксимирует стационарную задачу (15). Понятно, что при оптимизации шага по времени необходимо исходить из условия выхода на стационарное решение за наименьшее число шагов по времени. Для этого необходимо, чтобы начальные данные на каждом шаге затухали как можно сильнее.

Скорость затухания начальных данных можно исследовать методом разделения переменных. Нетрудно проверить, что собственные функции разностного оператора 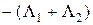в прямоугольной области и на равномерной сетке представляются в виде:

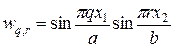, (19)

где q = 1,…, N -1, r = 1,…, M -1. Подставляя (19) в разностную схему (17) — (17¢¢) и полагая 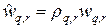, находим для множителя, описывающего рост гармоники, следующую формулу

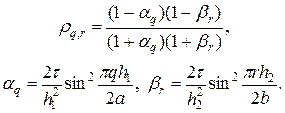(20)

На рис.2 (левый график) приведен типичный трехмерный профиль множителя роста 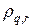в зависимости от номеров гармоник q и r, которые пробегают значения 1,…, N -1 и 1,…, M -1 соответственно. Из рисунка видно, что наиболее медленно убывающие гармоники, т.е. те гармоники, модули которых наиболее близки к единице, находятся в окрестности четырех точек (q, r): (1,1), (N -1, M -1), (N -1,1), (1, M -1). На правом рис.2 приведен график зависимости сомножителя 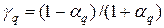от q, пробегающего значения 1,…, N -1. Видно, что сомножитель 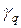по модулю меньше единицы и близок к единице в окрестности q = 1 и q = N -1. Считая параметр N достаточно большим, можно получить следующие оценки для сомножителя 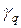в окрестности значений параметра q = 1 и q = N -1:

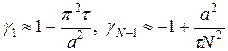. (21)

Аналогично ведет себя второй сомножитель 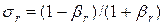, который по абсолютной величине максимален либо при r = 1, либо при r = M -1. В окрестности этих точек по аналогии с (21) и при M >> 1 можно записать:

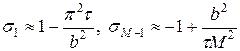. (21¢)

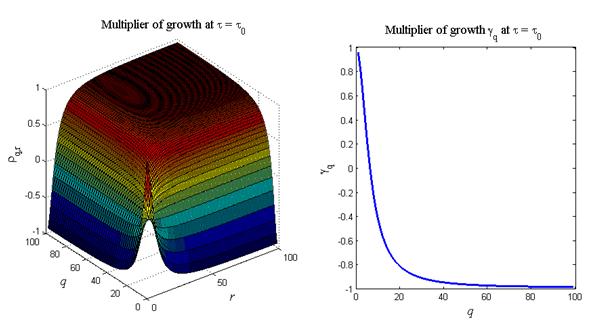
Рис.2. Трехмерный профиль множителя роста гармоник (20) и
зависимость множителя g_q от q

Перемножая попарно (21), (21¢), найдем четыре множителя роста 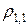, , 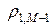, 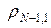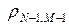наиболее приближенные по модулю к единице. На трехмерном профиле множителя роста, представленном на рис.2, отчетливо видны точки с максимально близкими по модулю значениями к единице. Найдем среднюю величину 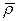из четырех этих значений, тогда

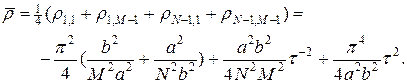(22)

Оптимальный шаг по времени t ₀ найдем, исходя из того, чтобы величина 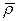была минимальной. Дифференцируя (22) по t и приравнивая результат к нулю, найдем оптимальное значение шага по времени

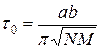. (23)

На листинге_№2 приведен код программы построения трехмерного профиля для множителя роста гармоник (20) в зависимости от номеров гармоник q и r. Кроме того, код программы строит график зависимости сомножителя g_q от q. Оба графика построены, исходя из оптимального значения (23) шага по времени t ₀. После отработки кода программы листинга_№2 должен появиться график, примерный вид которого приведен на рис.2.

Листинг_№2

%Программа построения трехмерного профиля

%множителя роста гармоник при переходе со

%слоя на слой в продольно-поперечной схеме и

%графика зависимости сомножителя gamma от q

clear all

a=1; b=1;%габариты прямоугольной области

N=100; M=100;%число узлов сетки по x1 и x2

h1=a/N; h2=b/M;%шаги равномерной сетки по x1 и x2

%Оптимальное значение шага по времени

tau=(a*b)/(pi*sqrt(N*M));

%Цикл построения трехмерного профиля множителя

%роста гармоник

for q=1:(N-1)

alpha=((2*tau)/h1^2)*sin((pi*q*h1)/(2*a))^2;

for r=1:(M-1)

beta=((2*tau)/h2^2)*sin((pi*r*h2)/(2*b))^2;

ro(q,r)=((1-alpha)*(1-beta))/...

((1+alpha)*(1+beta));

end

end

%Рисуем трехмерный профиль множителя роста

n1=1:(N-1); n2=1:(M-1);

subplot(1,2,1); surf(n2,n1,ro);

%Определяем зависимость gamma от q

for q=1:(N-1)

alpha=((2*tau)/h1^2)*sin((pi*q*h1)/(2*a))^2;

gamma(q)=(1-alpha)/(1+alpha);

end

%Рисуем график зависимости gamma от q

subplot(1,2,2); plot(n1,gamma);

Оценку величины оптимального шага в (23) следует рассматривать как довольно грубую. Например, в книге[1] величина оптимального шага оценивалась, исходя из уравнения 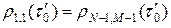, согласно которому

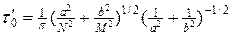. (23¢)

Оценки величины оптимального шага (23), (23¢) протестируем на примере решения двумерного эволюционного уравнения (16) с помощью продольно-поперечной разностной схемы. На листинге_№3 приведен соответствующий программный код.

Листинг_№3

%Программа численного определения величины

%оптимального шага по времени в процессе

%решения двухмерного уравнения теплопроводности

%(11) с помощью продольно-поперечной схемы

function optimum

global a b vc0 r0 r1

%Определяем габариты области интегрирования

%по времени, направлениям x1 и x2, а также

%константу vc0, задающую амплитуду

%начального распределения

a=1; b=1; vc0=100;

r0=0.2*min(a,b); r1=0.4*min(a,b);

%Задаем точность расчета на установление eps

eps=1e-8;

%Определяем число шагов по направлениям x1 и x2

N=41; M=41; h1=a/(N-1); h2=b/(M-1);

%Определяем сетки по x1 и x2

x1=0:h1:a; x2=0:h2:b;

%Оцеваем оптимальный шаг по формуле (23)

tau0=(a*b)/(pi*sqrt(N*M));

%Оцениваем оптимальный шаг по формуле (23')

tau1=(1/pi)*(a^2/N^2+b^2/M^2)^0.5*(1/a^2+1/b^2)^(-0.5);

%Выводим численные оценки величины оптимального шага

[tau0 tau1]

%Формируем массив шагов по времени

tau=(tau0/10):(tau0/10):(4*tau0);

k=0;

%Формируем цикл расчетов с различными шагами по времени

for tu=1:length(tau)

%Определяем начальные данные в виде кольца

for n=1:N

for m=1:M

y1(n,m)=v0(x1(n),x2(m));

end

end

%Организуем основной цикл интегрирования по времени

nrm=max(max(abs(y1)));

step(tu)=0;

%Формируем цикл по времени решения уравнения (16)

%на установление, т.е. до тех пор, пока не будет

%достигнута нужная точность eps

while (nrm>eps)&(step(tu)<300)

p1=(0.5*tau(tu))/h1^2;

p2=(0.5*tau(tu))/h2^2;

%Находим решение на полуцелом временном слое,

%т.е. решаем уравнение (11.39)

for m=2:(M-1)

%Учитываем нулевое граничное при x1=0

alpha(2)=0; beta(2)=0;

for n=2:(N-1)

alpha(n+1)=p1/(1+p1*(2-alpha(n)));

beta(n+1)=(y1(n,m)+p2*(y1(n,m-1)-...

2*y1(n,m)+y1(n,m+1))+p1*beta(n))/...

(1+p1*(2-alpha(n)));

end

%Учитываем нулевое граничное при x1=a

ys(N,m)=0;

for n=N:-1:2

ys(n-1,m)=alpha(n)*ys(n,m)+beta(n);

end

end

%Находим решение на следующем временном слое,

%т.е. решаем уравнение (11.39')

for n=2:(N-1)

%Учитываем нулевое граничное при x2=0

alpha(2)=0; beta(2)=0;

for m=2:(M-1)

alpha(m+1)=p2/(1+p2*(2-alpha(m)));

beta(m+1)=(ys(n,m)+p1*(ys(n-1,m)-...

2*ys(n,m)+ys(n+1,m))+p2*beta(m))/...

(1+p2*(2-alpha(m)));

end

%Учитываем нулевое граничное при x2=b

y2(n,M)=0;

for m=M:-1:2

y2(n,m-1)=alpha(m)*y2(n,m)+beta(m);

end

end

for m=1:M

y2(1,m)=0; y2(N,m)=0;

end

%Находим норму решения эволюционной задачи в L2

s=0;

for n=1:N

for m=1:M

s=s+h1*h2*y2(n,m)^2;

end

end

nrm=sqrt(s);

y1=y2;

step(tu)=step(tu)+1;

end

end

%Рисуем график зависимости числа шагов в задаче на

%установление с заданной точностью eps от шага

%интегрирования по времени

plot(tau,step);

%Определяем функцию начального распределения

function y=v0(x1,x2)

global a b vc0 r0 r1

r=sqrt((x1-0.5*a)^2+(x2-0.5*b)^2);

y=0;

if (r>=r0)&(r<=r1)

y=vc0*(r1-r)*(r-r0);

end

Работа программы листинга_№3 генерирует вывод двух чисел в командное окно MATLAB и графика, примерный вид которого приведен на рис.3. Пара чисел соответствует оценкам оптимального шага по двум формулам (23) и (23¢). Эти оценки довольно близки, отличия проявляются, когда N и M заметно отличаются. На рис.3 виден отчетливый минимум при выборе величины шага интегрирования по времени с помощью продольно-поперечной схемы. При данном конкретном значении параметров теоретические оценки оптимального шага по формулам (23) и (23¢) довольно близки к истинному значению, полученному из графика рис.3.

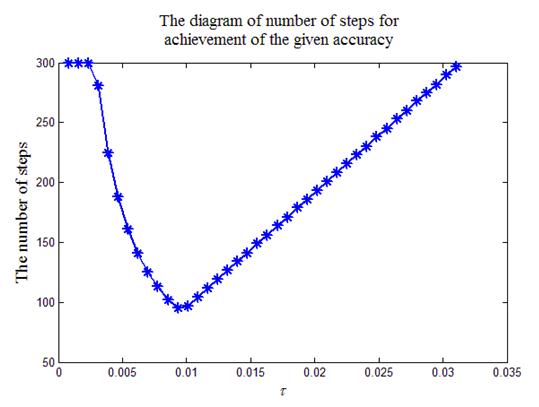
Рис.3. График зависимости числа шагов в продольно-поперечной схеме
для достижения заданной точности от шага сетки по времени

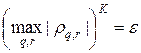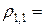
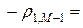
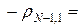
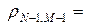
Минимальное число шагов K необходимое для достижения заданной точности e определяется из условия . Для оценки числа K выберем в качестве шага по времени — оптимальный шаг (23), а также предположим, что a = b и N = M, тогда нетрудно подсчитать согласно (20) — (21¢), что 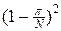, т.е.

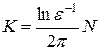или ,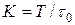

где T — время счета на установление (14). Таким образом, минимально необходимое число шагов по времени для достижения заданной точности реализуемое при оптимальном шаге (23) пропорционально числу узлов сетки по пространству.

Локально-одномерная схема (11.48), (11.49) с полусуммой по времени в двумерном случае допускает аналогичные выводы о наличии оптимального шага по времени для достижения заданной точности в счете на установление.

Действительно, представим локально-одномерную схему в виде:

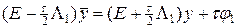, (24)

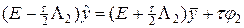, (24¢)

где операторы L₁, L₂ определены в (17¢¢) и коммутируют друг с другом. Умножим уравнение (24) слева на E + ½ t L₂, а уравнение (24¢) — на E — ½ t L₁, тогда, после исключения 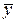, найдем

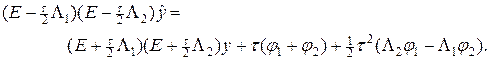
Последнее уравнение может быть преобразовано к канонической форме (17), т.е.

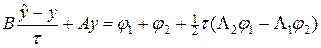, (25)

где операторы A и B определены в (17¢). Поскольку левая часть локально-одномерной схемы (25) совпадает с левой частью продольно-поперечной схемы (17), постольку минимальное количество шагов для достижения заданной точности в схеме на установление реализуется при некотором оптимальном шаге t ₀, оценка которого приведена в формулах (23), (23¢).

В общем случае, когда размерность два и более, область по пространству сложно устроена и пр., заранее неизвестно, какое число шагов необходимо совершить до установления. Поэтому на практике используют тот или иной нестрогий критерий установления. Без обсуждения приведем следующие три критерия сходимости:

,

,

.

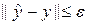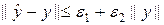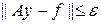Чебышевский набор шагов. Счет на установление может быть проведен с переменным шагом по времени. В задачах, в которых границы спектра разностных операторов известны, построены специальные наборы шагов t_k, k = 1,… K, обеспечивающие более быстрое затухание начальных данных, чем в случае расчетов с одним-единственным оптимальным шагом.

Пусть разностная схема может быть приведена к канонической двухслойной форме:

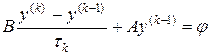, (26)

где, как обычно считается, что A и B — самосопряженные положительно определенные операторы, удовлетворяющие неравенствам

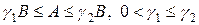. (27)

Затухание начальных данных определяется однородным уравнением (26) при j = 0. Обозначая решение однородного уравнения (26) символом z ^{( k )}, k = 1,…, K, перепишем его в форме

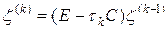, (28)

где

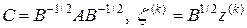. (28¢)

Согласно (28), имеем

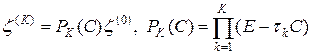. (29)

Из (29) видно, что для наиболее быстрого затухания начальных данных последовательность шагов t_k, k = 1,… K надо подобрать так, чтобы 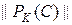была минимальна при заданном числе шагов K.

Поскольку A и B — самосопряженные операторы, оператор C также самосопряженный, причем согласно (27) следует следующая оценка:

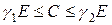. (30)

С учетом (30) норму операторного многочлена 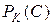можно оценить по формуле

,

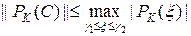где 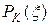— алгебраический многочлен. Известно, что многочлен, минимально уклоняющийся на отрезке 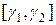от нуля, является многочленом Чебышева[2]. Учитывая это обстоятельство, можно использовать следующий чебышевский набор шагов:

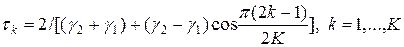. (31)

Считая многочлен 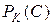многочленом Чебышева, можно оценить его максимальное отклонение от нуля согласно формуле:

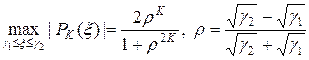. (32)

Отбросим 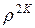в (32), считая что это слагаемое много меньше единицы, тогда число шагов K в схеме счета на установление (26) с чебышевским набором шагов по времени для достижения заданной точности e, можно представить в виде следующей формулы:

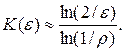(33)

Проиллюстрируем использование чебышевского набора шагов по времени на примере счета на установление с помощью явной разностной схемы вида

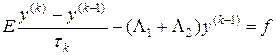. (34)

Схема (34) записана в канонической форме (26), поскольку B = E и A = - (L₁ + L₂). Найдем g ₁, g ₂, которые, согласно (27), определяют пределы изменчивости оператора A, т.е. 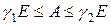. Для этого достаточно найти минимальное и максимальное собственные значения оператора A = - (L₁ + L₂). Задача на собственные значения оператора A решена в учебнике[3], где приведено следующее выражение для собственных значений

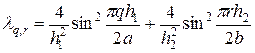. (35)

Учитывая, что q = 1,…, N -1 r = 1,…, M -1 в (35), найдем

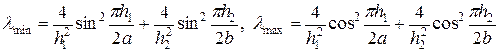. (36)

Учитывая, что 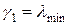и 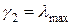, оценим по порядку величины число K в расчете на установление с чебышевским набором шагов. Для этого положим, что a = b, N = M >>1, тогда 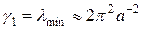, , 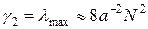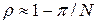. Подставляя значение r в (33), находим искомое число шагов для достижения заданной точности e:

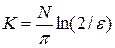. (37)

Оценка (37) говорит о том, что данная процедура эквивалентна экономичным схемам с постоянным оптимальным шагом.

Явная схема (34) устойчива только при условии, что 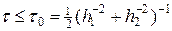. Среди чебышевского набора шагов (31) есть как большие 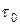, так и меньшие 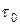. Большие шаги вызывают рост погрешности, меньшие — ее затухание. В целом же после K шагов ошибка уменьшится в 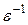. Ошибки на промежуточных шагах могут возрасти настолько сильно, что превысят пределы памяти, отводимые для чисел с плавающей запятой (в MATLAB под тип double отводится 64 бит или 8 байт) и расчет не удастся довести до конца. Для преодоления этой трудности необходимо выбирать шаги Чебышева в таком порядке, чтобы отдельный локальный рост в начальных данных был скомпенсирован соответствующим затуханием при последующих шагах. На листинге_№4 приведена небольшая программа, которая изображает последовательность чебышевских шагов (31) для разностной схемы (34) при некотором выборе параметров.

Листинг_№4

%Программа рисования набора чебышевских шагов

%(31) tau(k), k=1,2,...,K

clear all

%Определяем точность счета на установление

eps=1e-8;

%Определяем габариты области в плоскости x1 и x2

a=1; b=1;

%Определяем число узлов сеток по x1 и x2

N=101; M=301;

h1=a/(N-1); h2=b/(M-1);

%Пороговое значение шага, превышение которого

%приводит к неустойчивости при решении по

%разностной схеме (34)

tau0=(0.5*h1^2*h2^2)/(h1^2+h2^2);

%Определяем спектральные пределы оператора A

gm1=(4/h1^2)*sin((pi*h1)/(2*a))^2+...

(4/h2^2)*sin((pi*h2)/(2*b))^2;

gm2=(4/h1^2)*cos((pi*h1)/(2*a))^2+...

(4/h2^2)*cos((pi*h2)/(2*b))^2;

ro=(sqrt(gm2)-sqrt(gm1))/(sqrt(gm2)+sqrt(gm1));

%Определяем число шагов Чебышева K

K=fix(log(2/eps)/log(1/ro));

%Вычисляем шаги Чебышева

for k=1:K

tau(k)=2/((gm2+gm1)+...

(gm2-gm1)*cos((pi*(2*k-1))/(2*K)));

end

%Рисуем шаги Чебышева от номера k

semilogy(1:K,tau,'LineWidth',2);

hold on

%Рисуем линию, изображающую пороговое значение

%устойчивости разностной схемы (34)

semilogy(1:K,tau0*ones(1,K),'--',...

'LineWidth',3,'Color','red');

На рис.4 приведены значения шагов Чебышева при некотором выборе значений соответствующих параметров. Пунктирная линия на рис.4 обозначает порог устойчивости расчетов по разностной схеме (34). Видно, что приблизительно половина шагов из всего набора меньше порогового значения, а вторая половина больше.

Идея выбора определенной последовательности чебышевских шагов состоит в том, чтобы шаг роста неустойчивости был скомпенсирован на следующем шаге соответствующим ее уменьшением. Правило перестановки особенно просто, когда число шагов является степенью двойки. В этом случае шаги располагаем в естественном порядке и группируем парами: первый — последний, второй — предпоследний и т.д. Затем пары группируются в четверки: первая — последняя и т.д. Аналогично группируются восьмерки и т.д. Например, для 16 шагов искомый порядок таков:

{1, 16, 8, 9, 4, 13, 5, 12, 2, 15, 7, 10, 3, 14, 6, 11}. (38)

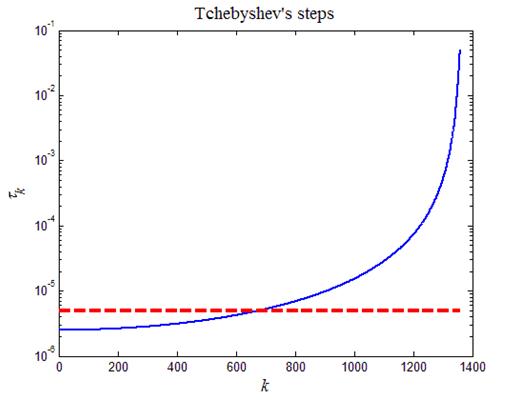
Рис.4. Чебышевский набор шагов при некотором выборе значений
соответствующих параметров

Возвращаемся к разностной схеме (34). Будем считать, что

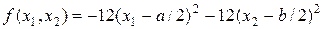, (39)

тогда уравнение

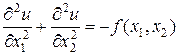(40)

имеет следующее решение

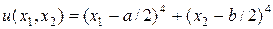. (41)

Уравнение (40) будем решать с помощью счета на установление по разностной схеме (34) с правой частью (41) и с последовательностью чебышевских шагов (38). Будем оценивать динамику ошибки

error _k = 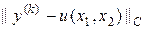, k = 1,…, K + 1, (42)

где 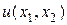— аналитическое решение (41). Код соответствующей программы представлен на листинге_№5.

Листинг_№5

%Программа оценки качества сходимости в схеме

%на установление (34) при специальном выборе

%последовательности чебышевских шагов

function cheb2

global a b

%Определяем точность счета на установление

eps=1e-2;

%Определяем габариты области в плоскости x1 и x2

a=1; b=1;

%Определяем число узлов сеток по x1 и x2

N=11; M=11;

h1=a/(N-1); h2=b/(M-1);

%Задаем сетки по x1 и x2

x1=0:h1:a; x2=0:h2:b;

%Определяем спектральные пределы оператора A

gm1=(4/h1^2)*sin((pi*h1)/(2*a))^2+...

(4/h2^2)*sin((pi*h2)/(2*b))^2;

gm2=(4/h1^2)*cos((pi*h1)/(2*a))^2+...

(4/h2^2)*cos((pi*h2)/(2*b))^2;

ro=(sqrt(gm2)-sqrt(gm1))/(sqrt(gm2)+sqrt(gm1));

%Определяем число шагов Чебышева K

K=fix(log(2/eps)/log(1/ro));

%Вычисляем шаги Чебышева

for k=1:K

tau(k)=2/((gm2+gm1)+...

(gm2-gm1)*cos((pi*(2*k-1))/(2*K)));

end

%Задаем порядок использования шагов Чебышева

ord=[1 16 8 9 4 13 5 12 2 15 7 10 3 14 6 11];

%Вычисляем аналитическое решение (41)

for n=1:N

for m=1:M

ya(n,m)=(x1(n)-0.5*a)^4+(x2(m)-0.5*b)^4;

end

end

%Определяем начальное условие для схемы (34)

for n=1:N

for m=1:M

y(1,n,m)=0;

end

end

%Задаем граничные условия при x2=0 и x2=b

for k=1:(K+1)

for n=1:N

y(k,n,1)=(x1(n)-0.5*a)^4+(x2(1)-0.5*b)^4;

y(k,n,M)=(x1(n)-0.5*a)^4+(x2(M)-0.5*b)^4;

end

end

%Задаем граничные условия при x1=0 и x1=a

for k=1:(K+1)

for m=1:M

y(k,1,m)=(x1(1)-0.5*a)^4+(x2(m)-0.5*b)^4;

y(k,N,m)=(x1(N)-0.5*a)^4+(x2(m)-0.5*b)^4;

end

end

%Определяем основной цикл расчета по схеме (34)

for k=2:(K+1)

p1=tau(ord(k-1))/h1^2; p2=tau(ord(k-1))/h2^2;

for n=2:(N-1)

for m=2:(M-1)

y(k,n,m)=y(k-1,n,m)+...

p1*(y(k-1,n-1,m)-2*y(k-1,n,m)+...

y(k-1,n+1,m))+p2*(y(k-1,n,m-1)-...

2*y(k-1,n,m)+y(k-1,n,m+1))+...

tau(ord(k-1))*f(x1(n),x2(m));

end

end

end

%Определяем величину ошибки (42) на

%каждом шаге расчетов

for k=1:(K+1)

for n=1:N

for m=1:M

z(n,m)=100*abs(y(k,n,m)-ya(n,m));

end

end

error(k)=max(max(z));

end

%Рисуем динамику ошибки от номера шага

semilogy(1:(K+1),error);

%Определяем функцию правой части (39)

function y=f(x1,x2)

global a b

y=-12*(x1-0.5*a)^2-12*(x2-0.5*b)^2;

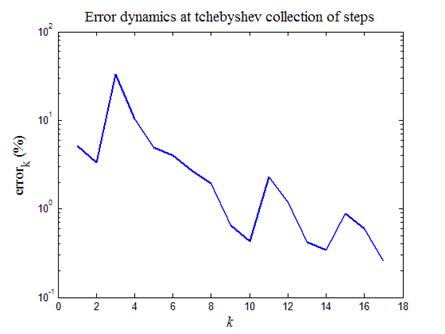
Рис.5. Динамика ошибки решения, полученная методом
установления (34), в зависимости от номера шага

После отработки кода программы листинга_№5 получится график, приведенный на рис.5. Итоговый график представляет динамику ошибки (42) в схеме на установление (34) в зависимости от номера шага с чебышевским набором шагов в последовательности (38). Из графика видно как ошибка совершает колебания, возникающие при чередовании шагов превышающих и не достигающих порога устойчивости. В целом же видно, что точность расчета существенно повышается к концу последнего шага и становится меньше заданной точности в 1%.