2014-02-09
1013
Интегральные уравнения
Лекция №14
Постановка задачи. Интегральным называют уравнение, в котором неизвестная функция u (x) входит под знак интеграла. В одномерном случае интегральное уравнение имеет следующий вид:
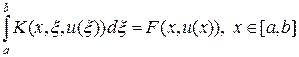, (1)
где ядро K (x, x, u) и правая часть F (x, u) считаются заданными функциями. Среди нелинейных интегральных уравнений общего вида (1) различают нелинейные уравнения Урысона и Гоммерштейна:
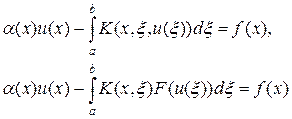
соответственно.
В качестве примера интегрального уравнения можно привести задачу восстановления переданного радиосигнала u (t) по принятому сигналу f (t) согласно решению интегрального уравнения типа свертки:
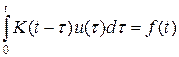. (2)
В (2) ядро K (x) определяется свойствами приемной аппаратуры и окружающей сигнал среды.
Отметим то обстоятельство, что уравнения в частных производных часто являются следствием законов сохранения, которые могут выступать в форме интегральных уравнений. Например, уравнения Навье-Стокса, используемые для описания сплошной среды, являются следствием законов сохранения массы, импульса и энергии плюс соответствующих условий гладкости, наложенных на неизвестные величины. Данное обстоятельство было неоднократно использовано в предыдущих лекциях при построении консервативных разностных схем.
Если переход от обыкновенных дифференциальных уравнений к уравнениям в частных производных является принципиальным усложнением, переход в интегральном уравнении к многомерному случаю естественен и состоит в формальной замене в (1) переменных x и x на соответствующие векторы x = (x 1,…, xp) Î G, x = (x 1,…, xp) Î G и проведении интегрирования по области G.
В дальнейшем рассмотрим некоторые частные случаи одномерного уравнения (1).
Наиболее хорошо изучены линейные интегральные уравнения, когда неизвестная функция u входит в интегральное уравнение линейно. Например, линейное уравнение
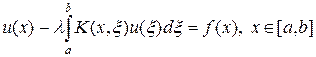, (3)
называют уравнением Фредгольма второго рода. Если ядро K (x, x) = 0 при x < x, т.е. ядро отлично от нуля на треугольной области, то уравнение (3) переходит в уравнение, которое принято называть уравнением Вольтерра второго рода:
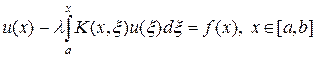. (4)
Если в уравнениях (3), (4) отбросить член u не входящий под знак интеграла, то получим уравнения Фредгольма и Вольтерра первого рода. Уравнения первого рода являются некорректно поставленными и будут рассмотрены далее специально. Уравнения второго рода являются корректными. Рассмотрим их более подробно.
Для однородного уравнения Фредгольма второго рода (3) ставится задача на собственные значения:
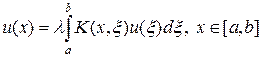. (5)
Задача на собственные значения (5) состоит в поиске таких l = li, при которых уравнение (5) имеет нетривиальные решения u = ji. В этом случае li называются собственными значениями ядра K (x, x), а ji — его собственными функциями. Если ядро вещественное и симметричное, т.е. K (x, x) = K (x, x) = K *(x, x), то оно имеет, по крайней мере, одно собственное значение. Все собственные значения такого ядра вещественны, а его собственные функции ортогональны друг другу. Отметим, что система функций ji может быть неполной и даже конечной.
Неоднородное уравнение Фредгольма (3) при значении параметра l, отличного от любого из собственных значений li ядра, имеет единственное решение u (x), которое для симметричного ядра может быть представлено в виде разложения Шмидта:
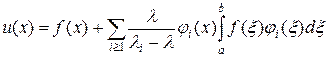. (6)
Если ядро K (x, x) и правая часть f (x) интегрируемы с квадратом, то ряд в (6) сходится абсолютно и равномерно. Из (6) видно, что при l ¹ li решение u (x) существует, единственно и непрерывно зависит от f (x), т.е. задача (3) корректна. Если параметр l равен одному из собственных значений li, тогда неоднородное уравнение Фредгольма (3) может не иметь решения или иметь их множество при специальном выборе правой части. Другими словами, при l = li задача (3) является некорректно поставленной.
Уравнение Вольтерра не имеет собственных значений, поэтому неоднородное уравнение (4) всегда имеет единственное решение.
Разностный метод. Проиллюстрируем использование разностного метода на примере численного решения нелинейного интегрального уравнения
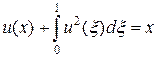, (7)
взятого с сайта[1]. Там же приведен аналитический метод решение уравнения (7), который дает пару решений:
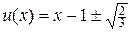. (7¢)
Введем сетки по переменным x и x Î [0,1]: xn = h (n - 1), n = 1,…, N, xm = hm, m = 1,…, N, h = 1/(N - 1). Аппроксимируем интеграл в (7) по формуле трапеции и запишем уравнение (7) в узлах сетки, тогда, считая, что yn» u (xn), получим
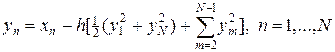. (8)
Нелинейную систему алгебраических уравнений (8) будем решать методом последовательных приближений по формуле
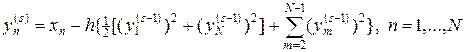, (9)
где s = 2,3,… — номер итерации в методе последовательных приближений, а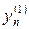 
— произвольное начальное приближение.
На листинге_№1 приведен код программы численного решения интегрального уравнения (7) методом последовательных приближений согласно схеме (9). Процедура повтора итераций прекращалась согласно критерию: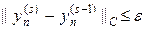 
, где e > 0 — малый параметр точности, который находится в нашем распоряжении.
Листинг_№1
%Численное решение интегрального уравнения (7)
%с помощью разностной схемы (9) в комплексе с
%методом последовательных приближений
clear all
%Определяем точность сходимости итераций eps и
%максимальное количество итераций smax
eps=1e-5; smax=30;
%Определяем число узлов в разностной схеме
%и шаг сетки
N=101; h=1.0/(N-1);
%Определяем сетку по x
x=0:h:1;
%Определяем начальное распределение решения
%в методе последовательных приближений
for n=1:N
y(n)=0.1*randn;
end
%Оцениваем отличие начального распределения
%решения от аналитического решения (7') в
%норме C
for n=1:N
z(n)=abs(y(n)-x(n)+1-sqrt(2.0/3));
end
error(1)=max(z);
%Рисуем начальное распределение в виде красной
%линии
subplot(1,2,1);
plot(x,y,'Color','red','LineWidth',1.5);
hold on
s=1; er=1;
%Организуем цикл последовательных приближений
%к искомому решению согласно схеме (9)
while (er>eps)&(s<smax)
for n=1:N
I=0.5*(y(1)^2+y(N)^2);
for m=2:(N-1)
I=I+y(m)^2;
end
y2(n)=x(n)-h*I;
end
%Находим разность между новой и предыдущей
%итерациями
for n=1:N
z(n)=abs(y2(n)-y(n));
end
%Оцениваем ошибку сходимости в норме C
er=max(z);
y=y2;
s=s+1;
subplot(1,2,1); plot(x,y,'LineWidth',1.5);
hold on
%Находим разность между текущей итерацией и
%аналитическим решением (7')
for n=1:N
z(n)=abs(y(n)-x(n)+1-sqrt(2.0/3));
end
error(s)=max(z);
end
%Определяем аналитическое решение
for n=1:N
ya(n)=x(n)-1+sqrt(2.0/3);
end
%Рисуем аналитическое решение черной жирной линией
subplot(1,2,1);
plot(x,ya,'Color','black','LineWidth',3);
%Рисуем график зависимости ошибки численного решения
%от шага итерации
subplot(1,2,2);
semilogy(1:s,error,'LineWidth',2);
На рис.1 приведен итог работы кода программы листинга_№1. На левом рисунке изображены графики последовательных итераций, которые сходятся к аналитическому решению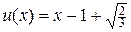 
. Случайная кривая, изображенная красной линией, выступала в качестве начального приближения в процедуре последовательных приближений. Черной жирной линией изображено аналитическое решение 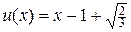. На правом графике изображена зависимость ошибки численного решения error = 
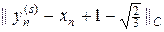от номера итераций. Видна довольно высокая скорость сходимости. Отметим, что второе аналитическое решение 
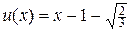не удается воспроизвести согласно численной процедуре (9), т.к. итерации расходятся.
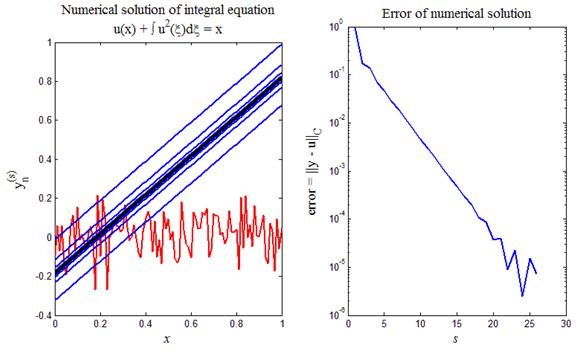
Рис.1. Численное решение интегрального уравнения (7) с помощью
метода последовательных приближений (9)
Рассмотрим далее линейные задачи. Для линейных задач обоснование сходимости содержится в теории Фредгольма, которая здесь не приводится из-за своей громоздкости[2]. Пусть для аппроксимации интеграла, взятого на отрезке [ a, b ], используется одна из линейных квадратурных формул с узлами xn, и весами cn, n = 1,…, N, т.е.
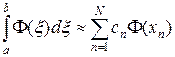. (10)
Применим формулу (10) к однородному уравнению Фредгольма (5), тогда получим
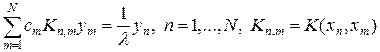. (11)
Система (11) представляет собой систему на определение собственных значений матрицы K ¢ с элементами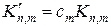 
. Матрица K ¢ имеет N собственных значений, которые являются приближением к первым собственным значениям ядра K (x, x). Разностное уравнение (11) решают с помощью методов, разобраны в лекции №6, посвященной проблеме собственных значений.
Изучим задачу (11) на примере решения однородного уравнения Фредгольма (5) с простейшим ядром K (x, x) = xx. Для данного ядра существует одно-единственное собственное значение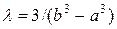 
и собственная функция u (x) = Cx, где C — произвольная константа. Выбирая формулу трапеции при аппроксимации интеграла, перепишем уравнение (11) для данного конкретного случая в следующем виде:
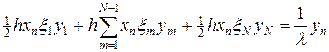, (12)
где xn = a + h (n - 1), xm = a + h (m - 1), n, m = 1,…, N, h = (b - a)/(N - 1). Задачу (12) на поиск собственных значений l -1 будем решать численно, используя встроенную в MATLAB функцию eig. На листинге_№2 приведен код соответствующей программы.
Листинг_№2
%Программа поиска собственного значения для
%однородного уравнения Фредгольма (5) согласно
%разностной схеме (12)
clear all
%Определяем отрезок интегрирования [a,b] и
%начальное значение для числа узлов сетки
a=0; b=1; N=4;
%Определяем цикл удвоения числа узлов сетки
for s=1:7
N=2*N; h=(b-a)/(N-1);
%Определяем сетки по x и xi
x=a:h:b; xi=a:h:b;
%Формируем матрицу левой части уравнения (12)
for n=1:N
A(n,1)=0.5*h*x(n)*xi(1);
for m=2:(N-1)
A(n,m)=h*x(n)*xi(m);
end
A(n,N)=0.5*h*x(n)*xi(N);
end
%Оцениваем численно собственное значение
lambda=1/max(eig(A));
%Численную ошибку оценки собственного значения
%делим на квадрат шага сетки
const(s)=abs((3.0/(b^3-a^3))-lambda)/h^2;
step(s)=h;
end
%Рисуем зависимость предстепенной константы от
%шага сетки
semilogx(step,const);
На рис.2 приведен итог работы кода программы листинга_№2. График изображает зависимость величины const в оценке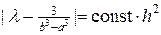 
ошибки приближенно вычисленного собственного значения l от шага сетки h. Из графика видно, что при шаге сетки, стремящемся к нулю, величина const действительно выходит на некоторое постоянное значение, т.е. разностная схема (12) обеспечивает второй порядок аппроксимации в оценке неизвестного собственного значения. Это не удивительно, т.к. формула трапеции, используемая при аппроксимации интеграла, имеет, как известно, второй порядок точности.
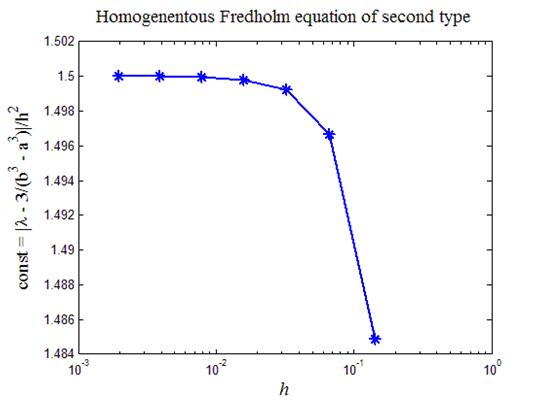
Рис.2. Оценка скорости сходимости численно найденного собственного значения
однородного уравнения Фредгольма второго рода к точному собственному значению
Учитывая аппроксимацию интеграла (10), для неоднородного уравнения Фредгольма второго рода (3) можно записать следующую разностную схему:
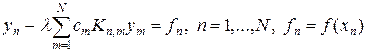. (13)
Система уравнений (13) легко может быть решена методом исключения Гаусса, когда l ¹ li, i = 1,…, N, где li, i = 1,…, N — собственные значения конечно-разностной задачи для соответствующего однородного уравнения Фредгольма второго рода. Обычно собственные значения ядра неизвестны. Поэтому для обнаружения и исключения случая l» li, i = 1,…, N, расчеты следует проводить на последовательности сгущающихся сеток. Если при сгущении сетки yn сходится к некоторому решению u (x), то это и есть искомое решение. Если на одной из сеток расчет выпадает из общей закономерности, то имело место случайное совпадение l» li. Если на всех сетках решение yn не сходится к пределу при h ® 0, то l» li.
Рассмотрим пример численного решения уравнения[3]
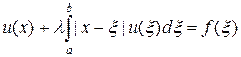, (14)
которое имеет точное, но довольно громоздкое решение. Аппроксимируем интеграл в (14) по формуле трапеции, тогда получим следующую разностную схему:
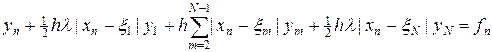, (15)
где n = 1,…, N. На листинге_№3 приведен код программы численного решения уравнения (14) по разностной схеме (15).
Листинг_№3
%Программа численного решения уравнения Фредгольма
%второго рода специального вида (14) по разностной
%схеме (15)
function fredh2
%Определяем константу lambda
lambda=-2;
%Определяем отрезок интегрирования [a,b] и
%начальное значение для числа узлов сетки
a=0; b=1; N=2;
%Определяем цикл расчетов с разными сетками
for s=1:9
N=N+3; h=(b-a)/(N-1);
%Определяем сетки по x и xi
x=a:h:b; xi=a:h:b;
%Формируем матрицу левой части уравнения (15)
for n=1:N
A(n,1)=0.5*h*lambda*abs(x(n)-xi(1));
for m=2:(N-1)
A(n,m)=h*lambda*abs(x(n)-xi(m));
end
A(n,N)=0.5*h*lambda*abs(x(n)-xi(N));
A(n,n)=A(n,n)+1;
end
%Определяем правую часть уравнения (15)
for n=1:N
F(n)=f(x(n));
end
%Решаем систему уравнений (15)
y=A\F';
%Рисуем полученное решение
plot(x,y,'LineWidth',(2*s-1)/s);
hold on
end
%Определяем правую часть уравнения (14)
function y=f(x)
y=sin(pi*x)^4;
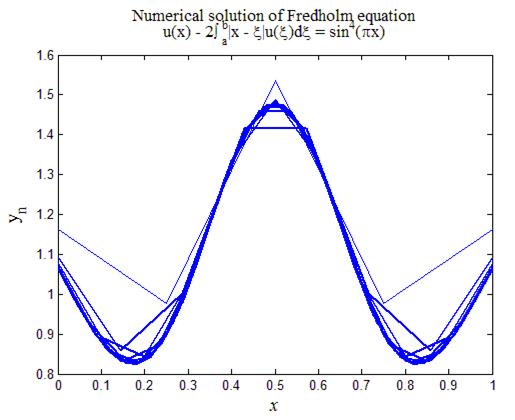
Рис.3. Численное решение уравнения Фредгольма второго рода (14)
по разностной схеме (15)
На рис.3 приведен итог работы кода программы листинга_№3. Расчеты проводились на различных все более сгущающихся сетках. Это отражено на рис.3 в виде все более утолщающихся линиях на все более подробных сетках. Видно, что численное решение yn сходится к некоторому решению по мере измельчения шага сетки h, т.е. выбранное значение l = -2 не является собственным значением ядра уравнения (14).
Уравнение Вольтерра (4) получается из уравнения Фредгольма (3) путем учета того, что K (x, x) = 0 при x < x. В этом случае алгебраическую систему уравнений (13) можно переписать в виде:
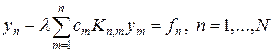. (16)
Система уравнений (16) решается обратным ходом метода Гаусса, поскольку обращаемая матрица является нижней треугольной.
Рассмотрим пример решения уравнения Вольтерра (4) по разностной схеме на примере решения уравнения
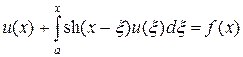, (17)
которое, согласно[4], имеет аналитическое решение
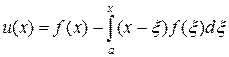. (18)
Как и выше воспользуемся квадратурной формулой трапеции, тогда разностная схема для решения уравнения (17) предстанет в виде:
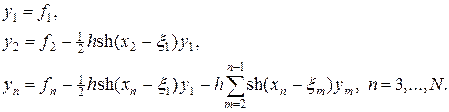(19)
На листинге_№4 приведен код программы численного решения уравнения Вольтерра (17) с помощью разностной схемы (19).
Листинг_№4
%Программа численного решения уравнения
%Вольтерра (17) по разностной схеме (19)
function volterra
%Определяем отрезок интегрирования [a,b] и
%начальное значение для числа узлов сетки
a=0; b=1; N=4;
%Определяем цикл расчетов с разными сетками
for s=1:8
N=N+6; h=(b-a)/(N-1);
%Определяем сетки по x и xi
x=a:h:b; xi=a:h:b;
%Вычисляем значения искомого решения
%согласно формулам (19)
y(1)=f(x(1));
y(2)=f(x(2))-0.5*h*sinh(x(2)-xi(1))*y(1);
for n=3:N
I=0;
for m=2:(n-1)
I=I+sinh(x(n)-xi(m))*y(m);
end
y(n)=f(x(n))-0.5*h*sinh(x(n)-xi(1))*y(1)-h*I;
end
%Рисуем полученное решение
plot(x,y,'LineWidth',(2*s-1)/s);
hold on
end
%Определяем правую часть уравнения (17)
function y=f(x)
y=sin(2*pi*x)^2;
На рис.4 приведен итоговый график работы кода программы листинга_№4. Расчеты проводились на серии все более сгущающихся сетках. Отчетливо видно, что численное решение, по мере измельчение шага сетки, сходится к решению уравнения Вольтерра. Сходимость иллюстрируется увеличивающейся толщиной линией изображающей численное решение для все более подробных сеток.
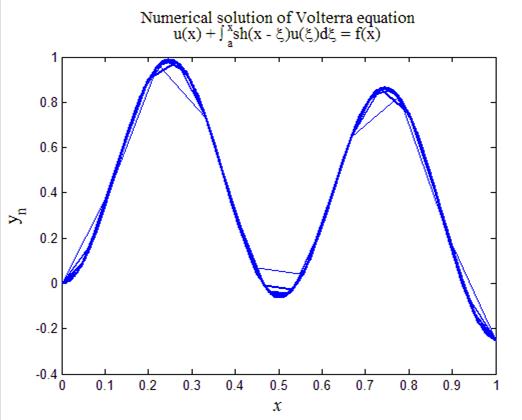
Рис.4. Численное решение уравнения Вольтерра (17) с помощью
разностной схемы (19)
Метод последовательных приближений. Для неоднородного уравнения Фредгольма второго рода (3) запишем итерационный процесс:
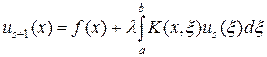, (20)
где s = 0,1,2,…, u 0(x) = 0 — нулевое начальное распределение для решения u. Покажем, что при ограниченном ядре и достаточно малом значении | l | итерационный процесс сходится к решению уравнения (3).
Доказательство. Определим погрешность s -й итерации через zs = us (x) - u (x). Вычитая (3) из (20), найдем
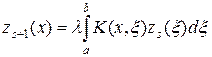. (21)
Согласно (21), можно получить следующую оценку:
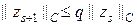, (22)
где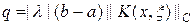 
. Таким образом, согласно (22), итерации при q < 1 сходятся равномерно по x, причем сходимость линейная. Последнее неравенство всегда можно обеспечить, выбирая достаточно малым параметр l.
Метод последовательных приближений для уравнения Вольтерра (4) сходится равномерно по x при любых значениях параметра l. Рассуждая аналогично предыдущему случаю, можно записать
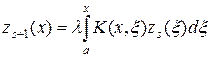. (23)
Проводя рассуждения, аналогичные доказательству сходимости метода Пикара (8.6) — (8.10), получим оценку
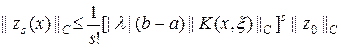. (24)
При s ® ¥ правая часть неравенства (24) стремится к нулю при любых значениях параметра l, что и доказывает наше утверждение.
Для примера рассмотрим численное решение уравнения Вольтерра (17) методом последовательных приближений, следуя формуле
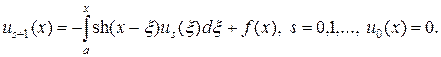(25)
Аппроксимируя интеграл, входящий в (25), по формуле трапеции, получим следующую расчетную схему:
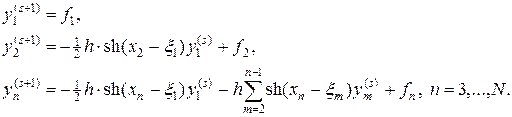(26)
На листинге_№5 приведен код программы, в которой решается уравнение Вольтерра (17) методом последовательных приближений в форме (25), (26). Итерационный процесс прерывался при условии, что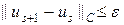 
, где e > 0 — параметр точности сходимости итераций.
Листинг_№5
%Программа численного решения уравнения
%Вольтерра (17) методом последовательных
%приближений согласно уравнению (25)
function volt_iter
%Определяем точность сходимости итераций eps и
%максимальное число итераций itmax
eps=1e-6; itmax=10;
%Определяем отрезок интегрирования [a,b]
a=0; b=1;
%Определяем число узлов в сетке и шаг сетки
N=101; h=(b-a)/(N-1);
%Определяем сетки по x и xi
x=a:h:b; xi=a:h:b;
%Определяем параметры итерационного процесса
er=1; iter=0;
%Рисуем начальную итерацию u0(x)=0 пунктирной
%линией
y=zeros(1,N); plot(x,y,'--');
hold on
%Организуем цикл итераций
while (er>eps)&(iter<itmax)
%Вычисляем значения y2 для s+1 итерации
%согласно формулам (26)
y2(1)=f(x(1));
y2(2)=f(x(2))-0.5*h*sinh(x(2)-xi(1))*y(1);
for n=3:N
I=0;
for m=2:(n-1)
I=I+sinh(x(n)-xi(m))*y(m);
end
y2(n)=f(x(n))-0.5*h*sinh(x(n)-xi(1))*y(1)-h*I;
end
%Оцениваем разницу s+1-й и s-й итераций в норме C
for n=1:N
z(n)=abs(y2(n)-y(n));
end
er=max(z);
iter=iter+1;
y=y2;
%Рисуем полученное решение
plot(x,y,'LineWidth',(3*iter-1)/iter);
hold on
end
%Выводим число итераций и ошибку er=||y(s+1) - y(s)||c
[iter er]
%Определяем правую часть уравнения (17)
function y=f(x)
y=sin(2*pi*x)^2;
На рис.5 приведен итог работы кода программы листинга_№5. Было осуществлено численное решение уравнения Вольтерра (17) методом последовательных приближений согласно расчетной формуле (26). Расчеты показали, что достаточно 6 итераций для достижения точности сходимости e = 10-6. На рис.5 пунктирной линией обозначена нулевая итерация u 0(x) = 0. Последующие итерации представлены линиями с все большей толщиной и, начиная с третьей итерации, в имеющемся масштабе линии уже не различаются. Таким образом, метод последовательных итераций является весьма эффективным для решения уравнений Вольтерра второго рода.
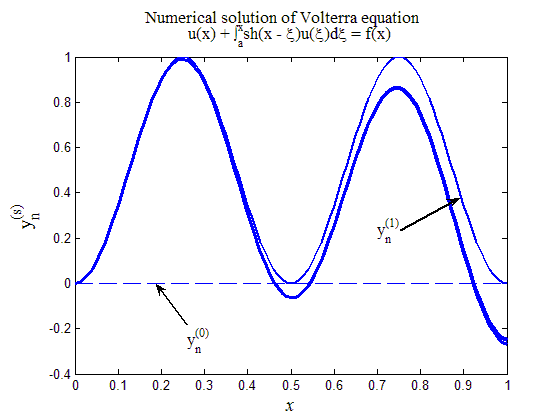
Рис.5. Численное решение уравнения Вольтерра (17) с помощью
метода последовательных приближений (25), (26)
Метод замены ядра вырожденным. Ядро уравнения Фредгольма называется вырожденным, если оно может быть представлено в виде конечной суммы
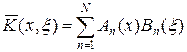. (27)
Решение уравнения Фредгольма с вырожденным ядром (27) осуществляется за конечное число шагов. Покажем это. Подставим ядро (27) в уравнение Фредгольма (3), тогда получим
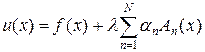, (28)
где
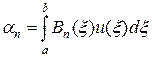. (29)
Подставляя (28) в (29), найдем систему N линейных уравнений для нахождения коэффициентов a 1,…, aN:
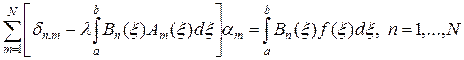. (30)
Из (28) — (30) следует, что вырожденное ядро (27) имеет ровно N собственных значений.
В качестве численного примера рассмотрим решение уравнения Фредгольма, имеющего следующий вид:
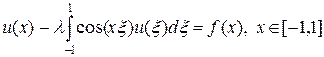. (30)
Ядро K (x, x) уравнения (30) может быть разложено в ряд Фурье по переменной x:
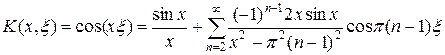. (31)
Рассмотрим теперь ограниченный отрезок ряда (31), отбросив бесконечный остаток, т.е. перейдем от ядра K (x, x) к вырожденному ядру
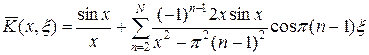. (32)
Заменяя в уравнении (30) ядро K (x, x) = cos(xx) на вырожденное ядро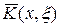 
, представленное в (32), получим уравнение относительно неизвестной функции y (x):
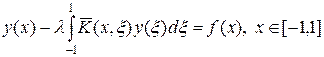. (33)
Изучим сходимость решения y (x) уравнения (33) к некоторому пределу при N ® ¥ путем решения системы линейных алгебраических уравнений (30) и восстановления решения по формуле (28). В этом случае можно считать, что
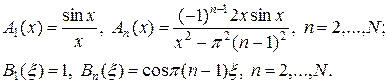(34)
На листинге_№6 приведен код программы решения интегрального уравнения (30) путем замены ядра cos(xx) на вырожденное ядро (32), полученное путем разложения ядра в ряд Фурье с последующим отбрасыванием бесконечного хвоста. Интегралы, входящие в (30), оценивались по формуле трапеции.
Листинг_№6
%Программа решения уравнения Фредгольма (30)
%путем замены ядра на вырожденное ядро (32), (33)
function degen_kernel
%Определяем параметр lambda, исходное число
%членов в разложении в ряд Фурье ядра, а также
%число расчетов с разным числом учтенных
%слагаемых в разложении ядра в ряд Фурье (32)
lambda=1; N=4; lmax=8;
%Определяем габариты области интегрирования
a=-1; b=1;
%Определяем число узлов сетки по аргументу x и xi
Nint=51; h=(b-a)/(Nint-1);
%Определяем сетки по x и xi
x=a:h:b; xi=a:h:b;
%Организуем цикл расчетов с разным числом учтенных
%слагаемых в разложении ядра в ряд Фурье (32)
for l=1:lmax
%Увеличиваем число слагаемых в разложении
%на единицу
N=N+1;
%Определяем систему линейных уравнений (30) в
%виде C alpha = d
for n=1:N
for m=1:N
I=0.5*B(n,xi(1))*A(m,xi(1))+...
0.5*B(n,xi(Nint))*A(m,xi(Nint));
for k=2:(Nint-1)
I=I+B(n,xi(k))*A(m,xi(k));
end
C(n,m)=-lambda*h*I;
if n==m
C(n,m)=C(n,m)+1;
end
end
I=0.5*B(n,xi(1))*f(xi(1))+...
0.5*B(n,xi(Nint))*f(xi(Nint));
for k=2:(Nint-1)
I=I+B(n,xi(k))*f(xi(k));
end
d(n)=h*I;
end
%Решаем систему уравнений C alpha = d
alpha=C\d';
%Определяем решение y по формуле (28)
for k=1:Nint
s=0;
for n=1:N
s=s+alpha(n)*A(n,x(k));
end
y(l,k)=f(x(k))+lambda*s;
end
end
%Рисуем численное решение исходного интегрального
%уравнения с максимальным числом учтенных
%слагаемых в разложении ядра в ряд Фурье
subplot(1,2,1); plot(x,y(lmax,:));
%Находим разницу между последующей и предыдущей
%итерациями в норме C
for l=1:(lmax-1)
for k=1:Nint
z(k)=abs(y(l+1)-y(l));
end
er(l)=max(z);
end
%Рисуем динамику разности последующей и
%предыдущих итераций в норме C от N -
%числа учтенных слагаемых в разложении (32)
subplot(1,2,2); semilogy(1:(lmax-1),er);
%Определяем функцию A(n,x)
function y=A(n,x)
if n==1
if x==0
y=1;
else
y=sin(x)/x;
end
else
y=((-1)^(n-1)*2*x*sin(x))/...
(x^2-(pi*(n-1))^2);
end
%Определяем функцию B(n,xi)
function y=B(n,xi)
if n==1
y=1;
else
y=cos(pi*(n-1)*xi);
end
%Определяем правую часть интегрального уравнения
function y=f(x)
y=sin(pi*x^2);
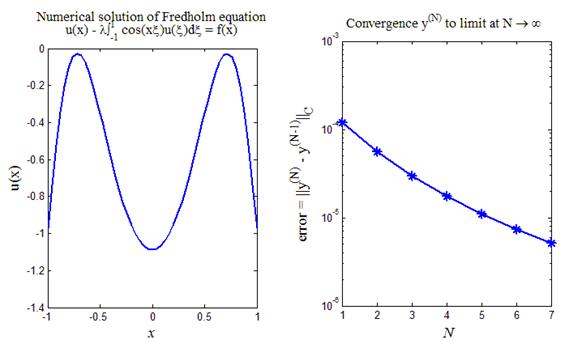
Рис.6. Численное решение уравнения Фредгольма (30) путем
замены ядра уравнения на вырожденное ядро(32)
На рис.6 приведен итог работы кода программы листинга_№6. На левом рисунке приведено численное решение интегрального уравнения Фредгольма (30) методом замены ядра на вырожденное ядро (32), полученное путем разложения исходного ядра в ряд Фурье с последующим отбрасыванием бесконечного хвоста разложения. Расчетов проводилось несколько с различным числом оставленных слагаемых N в разложении (32). Численное решение y ( N ) уравнения (33), полученное при некотором N сравнивалось с предыдущим, т.е. с y ( N -1) на предмет сходимости к некоторому пределу при N ® ¥. На правом рисунке приведена зависимость ошибки error =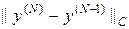 
от числа учтенных слагаемых N. Можно наблюдать довольно быстрое стремление ошибки к нулю и соответственно сходимость численного y ( N ) решения к некоторому пределу при N ® ¥.
