2014-02-10
843
Обратимся к формуле (6.6) и рис. 6.5, которые отражают результаты расчета магнитного поля прямолинейного провода с постоянным током. Выразим циркуляцию индукции магнитного поля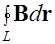 
вдоль контура, совпадающего с выделенной линией индукции магнитного поля (окружностью на рис. 6.5). Обозначим 
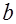- радиус окружности. Так как величина 
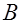остается постоянной вдоль этой окружности, а вектор 
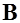- касательный к окружности в каждой точке, то
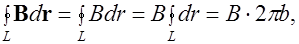
или, с учетом (6.6),
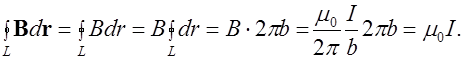(6.14)
Можно показать (см. Матвеев А.Н.), что формула (6.14) остается справедливой, если в качестве контура интегрирования выбрать не линию индукции магнитного поля, а произвольный замкнутый контур, охватывающий провод с током. В частности, если контур не охватывает провод с током, то в (6.14) надо положить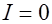 
. Тогда циркуляция 
.
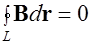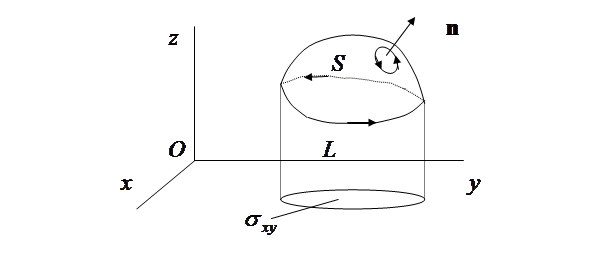
Силу тока в проводе выразим как интеграл от плотности тока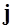 
по поверхности 
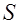(см. рис. 1.19)):
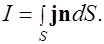(6.15)
