Магнитное поле движущегося заряда. Поверхность опирается на контур

Рис. 1.19. К формуле Стокса

Поверхность 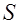опирается на контур 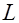. Для постоянного тока величина интеграла в (6.15) не зависит от выбора формы поверхности 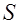в силу закона сохранения электрического заряда.

Подставим (6.15) в (6.14), найдем

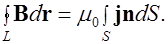(6.16)

Из теории электромагнетизма следует, что формула (6.16) остается справедливой не только в случае прямолинейного тока, но и для произвольного распределения плотности постоянного тока на поверхности .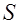

Пусть имеется система токов, распределенных в пространстве с плотностями 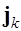, 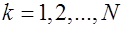. Обозначим 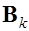- индукция магнитного поля, созданного 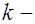ым током. По принципу суперпозиции, индукция результирующего поля 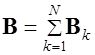, а плотность результирующего тока 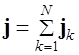. Применяя формулу (6.16) для 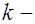ого тока, имеем:

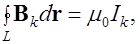(6.17)

где 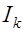- сила тока 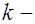ой компоненты через поверхность ,

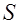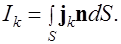(6.18)

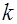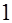Алгебраически суммируя равенства (6.17) по от до 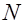, получим

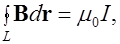(6.19)

где 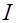сила полного тока через поверхность 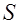, равная .

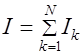Равенство (6.19) выражает формулу полного тока в интегральной форме.

Применим формулу Стокса для магнитного поля: поток вихря 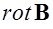векторного поля 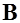через кусочно-гладкую поверхность 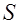, ограниченную замкнутым контуром 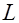, равен циркуляции вектора 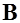по этому контуру.

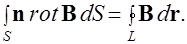(6.20)

Подставим (6.16) в (6.20), найдем

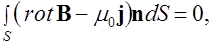
откуда в силу произвольности выбора поверхности 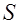следует

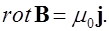(6.21)

Равенство (6.21) выражает формулу полного тока в дифференциальной форме. Из (6.21) следует, что в области, где нет токов (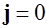) имеем: 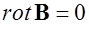. Аналогично условию 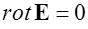для электростатического поля равенство 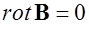выражает условие потенциальности постоянного магнитного поля в области, где нет токов.

Применим формулу полного тока (6.19) для расчета магнитного поля внутри тороидальной катушки, показанной на рис. 6.7. По виткам катушки течет постоянный ток силой 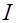. Пунктирная окружность радиуса 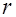, имеющая общий центр с катушкой, соответствует одной линий индукции магнитного поля катушки. Внутренний радиус катушки 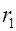, а внешний - 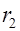. В силу симметрии катушки индукция магнитного поля постоянна по величине вдоль пунктирной окружности. Значит циркуляция индукции вдоль этой линии индукции 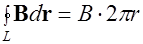. Та же окружность охватывает ток силой 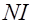, где 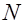- число витков катушки. По формуле полного тока имеем: 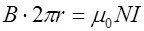. Значит, индукция магнитного поля тороидальной катушки на расстоянии 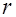от ее центра равна

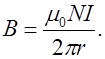
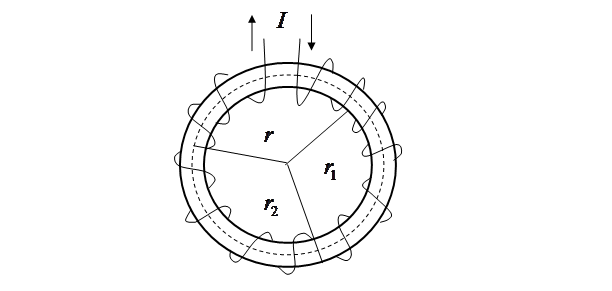
Рис. 6.7. Тороидальная катушка

Будем неограниченно увеличивать радиус 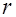тороида. Тогда отношение 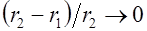, и поле стремится к однородному. Любой отрезок тороида стремится по форме к прямолинейной катушке – соленоиду. Заметим, что 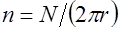- число витков на единицу длины соленоида, что дает выражение индукции магнитного поля соленоида:

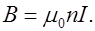
Пусть постоянный ток создается направленным движением свободных зарядов. Обозначим 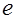- заряд одного носителя тока, 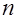- концентрация носителей тока, 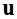- скорость направленного движения носителя тока. Выразим элемент тока

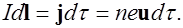(6.22)

Подставим (6.22) в формулу (6.4), выражающую индукцию магнитного поля, созданного элементом тока, найдем

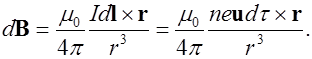(6.23)

В объеме 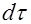находится 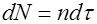частиц. Индукция 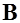магнитного поля, созданного одним движущимся зарядом, равна 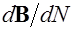, то есть

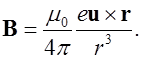(6.24)

Формула (6.24) показывает, что, как и магнитное поле прямого провода с током, поле движущегося заряда обладает осевой симметрией (относительно направления скорости 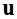движения заряда).