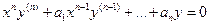 (1)
(1)
х=0 – особая точка уравнения (1)
Решение этого уравнения существует и единственно при 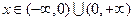 .
.
Будем рассматривать уравнение (1) при 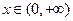 .
.
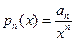 . Поэтому, согласно №14:
. Поэтому, согласно №14: 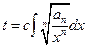 (2),
(2), 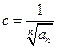 .
.
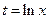 или
или 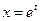 (3).
(3).
Тогда
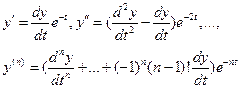 (4).
(4).
Подставляя (4) в уравнение (1), получаем однородное линейное уравнение n-го порядка с постоянными коэффициентами. Найдя общее решение и полагая в нём 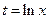 , мы получим общее решение уравнения Эйлера.
, мы получим общее решение уравнения Эйлера.
Пример 1. 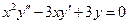 .
.
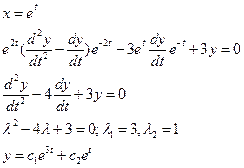
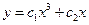 - общее решение однородного уравнения Эйлера.
- общее решение однородного уравнения Эйлера.
Пример 2. 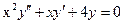
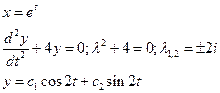
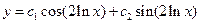 - общее решение уравнения Эйлера.
- общее решение уравнения Эйлера.
 2014-02-10
2014-02-10 477
477








