Приведение однородного линейного уравнения n-го порядка к уравнению с постоянными коэффициентами при помощи замены независимой переменной

Рассмотрим линейное однородное уравнение 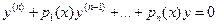(1).

Сделаем замену независимой переменной :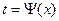

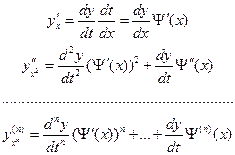(2)

Подставим (2) в (1) и разделим на 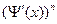, получим: 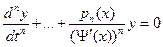(3).

Необходимо, чтобы 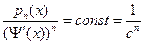(4), следовательно:

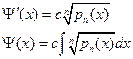(5).

Пример. Уравнение Чебышева.

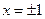- особые точки уравнения, .

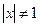Построим общее решение уравнения Чебышев при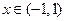

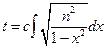(7). Возьмём 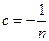, тогда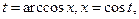 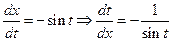; (8)

Подставляя (8) в уравнение Чебышева (6), получаем:

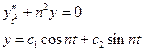
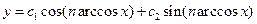(9) – общее решение уравнения (6)