Метод Коши

Метод вариации произвольных постоянных (метод Лагранжа).

Теорема:

Общее решение неоднородного уравнения 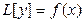(1) можно найти в квадратурах, если известно общее решение соответствующего однородного уравнения 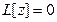(2)

 Будем искать общее решение уравнения (1) в виде 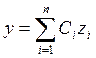(3), где {z_i} i=1,2..n – ФСР уравнения (2).

Найдём производные выражения (3), подчиняя их n-1 условиям:

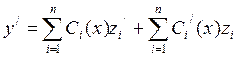, второе слагаемое равно нулю,

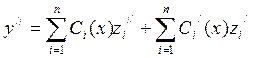, второе слагаемое равно нулю,

…… (4)

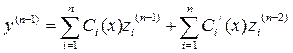, второе слагаемое равно нулю,

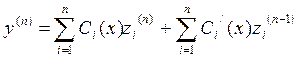
Подставляя (3) и (4) в уравнение (1), получим:

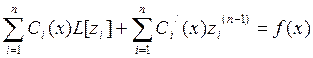(5)

Так как 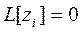, то окончательно получим

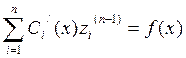(6)

Итак, для определения С_i(x) получаем следующую систему из n дифференциальных уравнений:

,

,

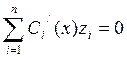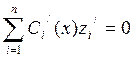…… (7)

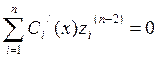
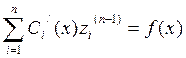
Система (7) является линейной неоднородной относительно С_i ^/ (x) с определителем равным W(x)¹0 в интервале (a,b).

Решая систему (4) по правилу Крамера получаем:

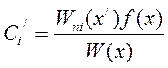, i=1,2…n; (8)

где W_{n i} – алгебраические дополнения к элементам n–ой строки определителя W(x).

Из 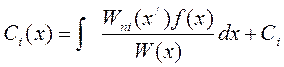, i=1,2…n; (9)

где C_i– произвольные постоянные, а " x₀ Î (a,b).

Подставляем (9) в выражение (3), получим:

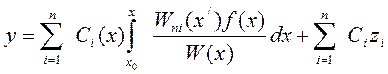, (10)

Пример:

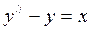
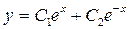– общее решение однородного уравнения.

Решение неоднородного уравнения ищем в виде: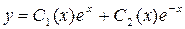

Составим систему для нахождения 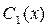и :

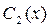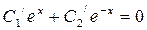
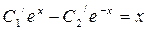Þ ,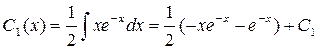

.

.

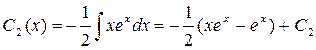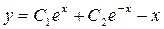Укажем ещё один способ построения частного решения уравнения 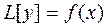(1).

Пусть {z_i} i=1,2..n – ФСР уравнения L[y]=0 (2)

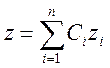(3) – общее решение уравнения (2).

Построим решение уравнения (2), удовлетворяющее следующим начальным условиям:

z = 0, z^/ = 0, …, z^(n-2) =0, z^(n-1) =1 при x = a, где "aÎ(a,b), xÎ(a,b).

Это решение 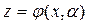(5)

Причём , , …, , ,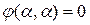

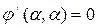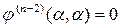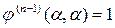где 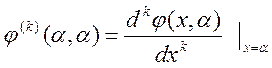, (6)

Докажем, что функция

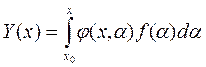, (7)

где " x₀ Î (a,b).

является частным решением уравнения (1) с нулевыми начальными условиями, т.е. Y = 0, Y^/ = 0, …, Y^(n-1) =0, при x = x₀.

Найдём значения производных функции Y(x):

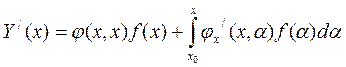, первое слагаемое = 0,

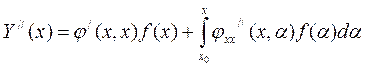, первое слагаемое = 0, …… (8)

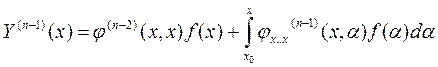, первое слагаемое = 0,

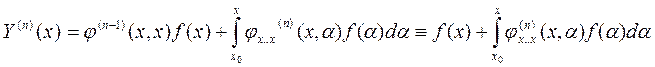и ,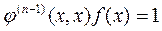

Подставим выражение (8) в уравнение (1):

+……

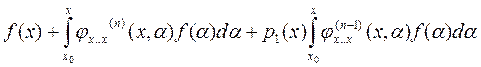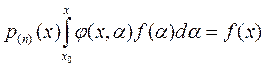…+ (9)

или

,

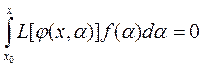Получим тождество для " x, x₀ Î(a,b).

Итак, 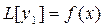, x Î(a,b).

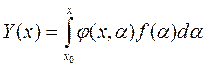(7) –называется формулой Коши для неодноролного уравнения.

Очевидно, что Y(x₀) = 0, Y^/ (x₀)= 0, …, Y^(n-1) (x₀)=0.

Таким образом .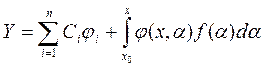

Пример:

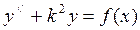
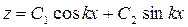– общее решение однородного уравнения.

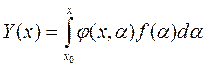
Найдём j (x,a)

z=0, z^/=1 при x = a.

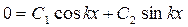
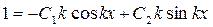Þ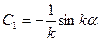

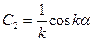
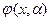
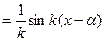
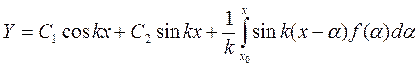
– oбщeе решение неоднородного уравнения.

ЛЕКЦИЯ 4: