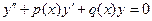 (1)
(1)
1. Сделаем замену 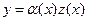 (2), где z(x) – новая неизвестная функция,
(2), где z(x) – новая неизвестная функция, 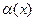 - дважды дифференцируемая в интервале непрерывности коэффициентов уравнения (1).
- дважды дифференцируемая в интервале непрерывности коэффициентов уравнения (1).
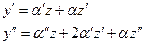 (3).
(3).
Подставим (3) в уравнение (1) и разделим на 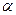 . Получим:
. Получим:
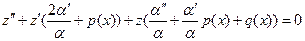 (4).
(4).
Приравняем коэффициент при 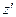 к нулю.
к нулю.
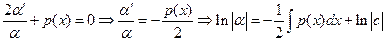
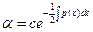 (5).
(5).
Положим С=1: 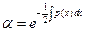 (5’).
(5’).
Таким образом, 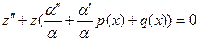 (6)
(6)
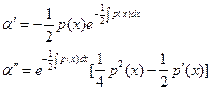 (7).
(7).
Тогда уравнение (6) принимает вид: 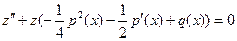 (8).
(8).
Функция 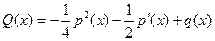 называется инвариантом уравнения (1).
называется инвариантом уравнения (1).
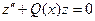 (8’).
(8’).
Если интегрируется уравнение (8’), то интегрируется и уравнение (1).
Очевидно, что если Q(x)=const, или 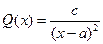 , то (8’) интегрируется в квадратурах.
, то (8’) интегрируется в квадратурах.
Пример. 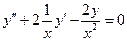
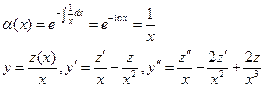
Подставляя значение функции и её производных в исходное уравнение, получаем
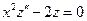 - уравнение Эйлера
- уравнение Эйлера
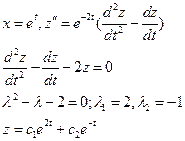
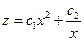 - общее решение данного уравнения.
- общее решение данного уравнения.
2. Избавимся от члена с первой производной, делая замену независимой переменной.
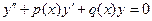 (1).
(1).
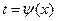 (9)
(9)
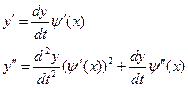 (10).
(10).
Подставим (10) в уравнение (1) и разделим на 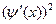 . Получим:
. Получим: 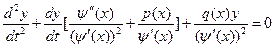 (11).
(11).
Приравняем коэффициент при 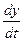 к нулю.
к нулю.
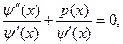
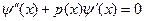 (12).
(12).
Интегрируя уравнение (12), получим, что 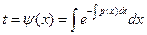 (13).
(13).
Уравнение (1), заменой (13), приводится к виду
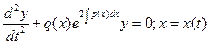 (14), не содержащему первой производной.
(14), не содержащему первой производной.
Пример. 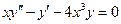 (15)
(15)
Сделаем замену (13): 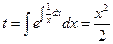 .
.
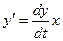
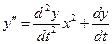 (16)
(16)
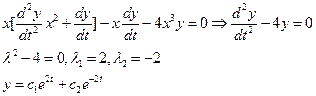
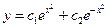 - общее решение уравнения (15).
- общее решение уравнения (15).
 2014-02-10
2014-02-10 882
882








