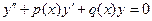 (1).
(1).
У1 – частное решение уравнения (1), т.е. L[y] = 0.
Сделаем замену 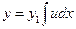 (2)
(2)
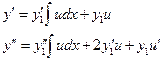 (3).
(3).
Подставим (3) и (2) в (1). Получим
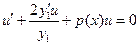 (4)
(4)
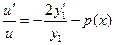 (5)
(5)
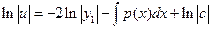
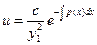 (6). Положим с=1, тогда:
(6). Положим с=1, тогда: 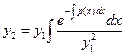 (7).
(7).
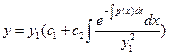 (8) - общее решение уравнения (1).
(8) - общее решение уравнения (1).
Пример. 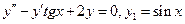 (9).
(9).
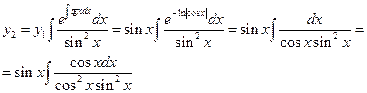
Рассмотрим:
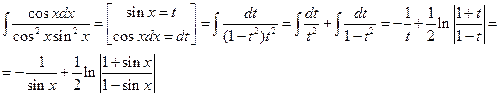
Таким образом: 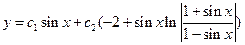 - общее решение уравнения (9).
- общее решение уравнения (9).
ЛЕКЦИЯ 6:
18. Интегрирование при помощи степенных и обобщённых степенных рядов.
Определение: Функция называется голоморфной в точке 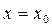 , если она представима в точке
, если она представима в точке 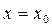 , т.е.
, т.е. 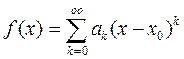 , причём ряд сходится в интервале
, причём ряд сходится в интервале 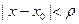 , (
, (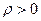 ).
).
Сформулируем теорему Коши для линейного дифференциального уравнения n-ого порядка:
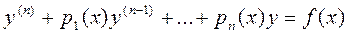 (1).
(1).
Заданы начальные условия 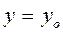 ,
, 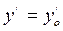 ,…,
,…,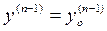 при
при 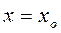
Теорема Коши:
Если все функции 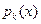 и
и 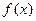 являются голоморфными в точке
являются голоморфными в точке 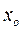 , т.е.
, т.е. 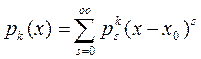 ,
, 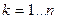 ,
, 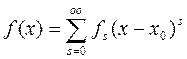 -сходятся в области
-сходятся в области 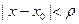 . Тогда существует единственное решение с заданными начальными условиями, голоморфными в области
. Тогда существует единственное решение с заданными начальными условиями, голоморфными в области 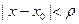 ,
,
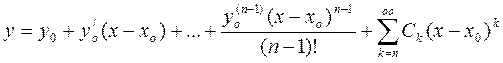 (2)
(2)
Рассмотрим линейное однородное уравнение второго порядка.
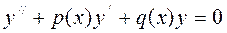 (3)
(3)
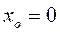 ,
, 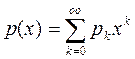 ,
, 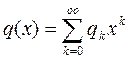 ,
,
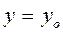 ,
, 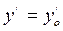 при
при 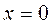 (3)
(3)
Тогда на основании теоремы Коши существует единственное голоморфное в окрестности 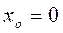 решение
решение 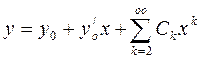 (4)
(4)
Подставим решение (4) в уравнение (3):
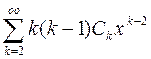 +
+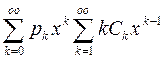 +
+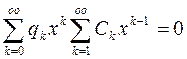 (5)
(5)
или
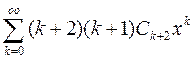 +
+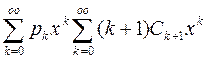 +
+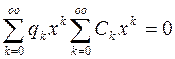 (6)
(6)
Воспользуемся формулой произведения степенных рядов.
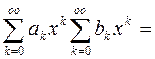
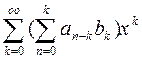 (7)
(7)
Тогда уравнение (6) имеет вид:
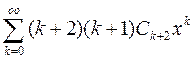 +
+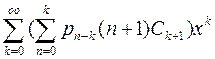 +
+ 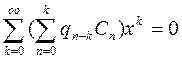 (8)
(8)
Приравнивая коэффициенты при одинаковых степенях, получим:
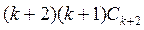 +
+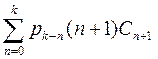 +
+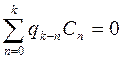 (9)
(9)
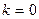 :
: 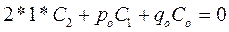 , находим С2
, находим С2
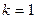 :
: 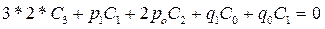 , находим С3.
, находим С3.
И так далее.
Коэффициенты находятся единственным образом.
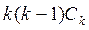 +
+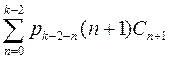 +
+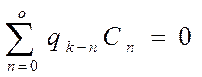
Пусть 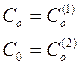 ,
, 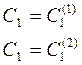 и
и 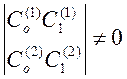 ,
,
Тогда мы получим два частные решения 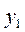 и
и 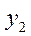 , которые образуют в интервале
, которые образуют в интервале 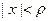 фундаментальную систему.
фундаментальную систему.
Следовательно, общее решение 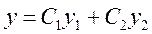 построено в окрестности точки
построено в окрестности точки 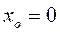 , которая называется обыкновенной.
, которая называется обыкновенной.
Точка 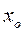 называется обыкновенной, если все коэффициенты уравнения голоморфны в этой точке, в противном случае, точку
называется обыкновенной, если все коэффициенты уравнения голоморфны в этой точке, в противном случае, точку 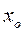 будем называть особой точкой дифференциального уравнения.
будем называть особой точкой дифференциального уравнения.
На практике удобно брать фундаментальную систему решений??? в точке 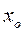 .
.
В нашем случае 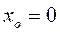 .
.
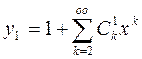 (10)
(10)
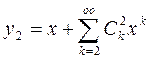 ,
,
определяя коэффициенты 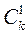 и
и 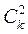 по формуле (9).
по формуле (9).
Пример 1:
Рассмотрим уравнение Эйри:
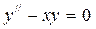 (11)
(11)
очевидно, что 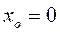 обыкновенная точка.
обыкновенная точка.
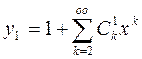 ,
, 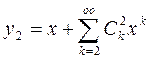 (12)
(12)
Подставим (12) в уравнение (11):
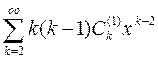
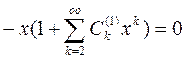
Приравнивая коэффициенты при одинаковых степенях, получим:
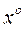 :
: 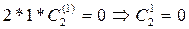
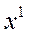 :
: 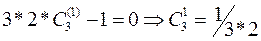
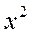 :
: 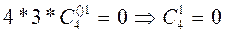
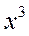 :
: 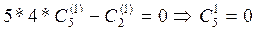
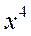 :
: 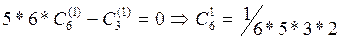
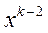 :
: 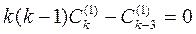
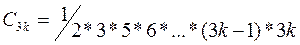
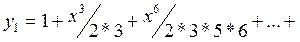
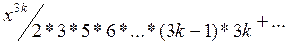
Аналогично находим 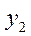 :
:
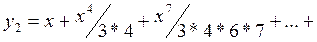
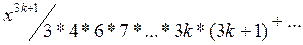
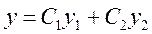 - общее решение уравнения Эйри.
- общее решение уравнения Эйри.
Рассмотрим уравнение Бесселя n-ого порядка:
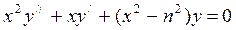 (13),
(13),
когда 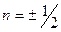
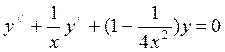 (14)
(14)
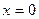 -особая точка.
-особая точка.
Пусть 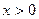 , замена
, замена 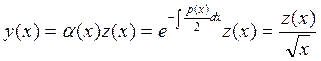 (15)
(15)
Приводим уравнение (14) к уравнению:
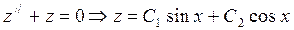
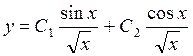 (16)
(16)
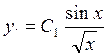 ,
,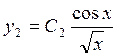 или
или
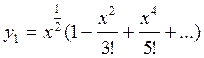 (17)
(17)
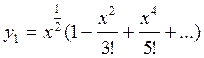
Функция Бесселя порядка:
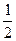 :
: 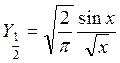 (18)
(18)
- :
: 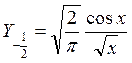
Ни 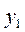 , ни
, ни 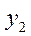 не являются голоморфными решениями в окрестности точки
не являются голоморфными решениями в окрестности точки 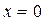 . Этого следовало ожидать, т.к.
. Этого следовало ожидать, т.к. 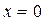 является особой точкой.
является особой точкой.
Обобщённым степенным рядом по степеням 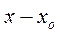 называется ряд вида
называется ряд вида 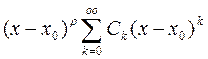 , где показатель ρ есть некоторое постоянное число, а ряд
, где показатель ρ есть некоторое постоянное число, а ряд 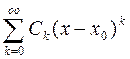 есть сходящийся степенной ряд, причём
есть сходящийся степенной ряд, причём 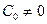 .
.
Какой вид должны иметь коэффициенты уравнения 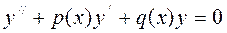 (1) в окрестности особой точки
(1) в окрестности особой точки 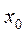 , чтобы хоть одно из частных решений было представимо в окрестности этой особой точки в виде обобщённого степенного ряда по степеням
, чтобы хоть одно из частных решений было представимо в окрестности этой особой точки в виде обобщённого степенного ряда по степеням 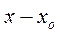 , т.е.
, т.е. 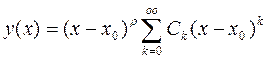 ,
, 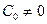 (19)
(19)
Ответ на этот вопрос даёт следующая теорема:
Теорема:
Для того, чтобы уравнение (1) имело в окрестности точки 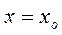 хоть одно частное решение в виде обобщённого степенного ряда (19), достаточно, чтобы это уравнение имело вид:
хоть одно частное решение в виде обобщённого степенного ряда (19), достаточно, чтобы это уравнение имело вид:
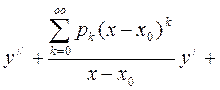
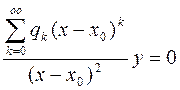 , (20)
, (20)
где 
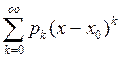 ,
, 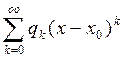 сходящиеся степенные ряды при
сходящиеся степенные ряды при 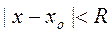 , причём
, причём 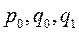 не равны нулю одновременно, ибо в противном случае точка
не равны нулю одновременно, ибо в противном случае точка 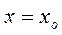 не особая и существует два линейно независимых решения, голоморфных в точке
не особая и существует два линейно независимых решения, голоморфных в точке 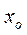 , и ряд
, и ряд 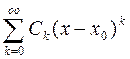 заведомо сходится в той же области.
заведомо сходится в той же области.
ЛЕКЦИЯ 7.
 2014-02-10
2014-02-10 611
611








