2014-02-10
637
Одной из первых задач, связанной с интегральными уравнениями, была задача обращения интеграла.
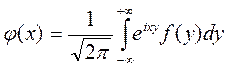(1).
Решение этой задачи получил Фурье:
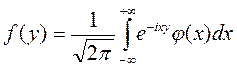(2)
К интегральным уравнениям типа Вольтера приводит задача Коши для обыкновенного дифференциального уравнения.
, 
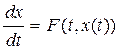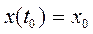(3)
Если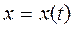 
есть решение дифференциального уравнения (3), то подставляя 
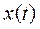в уравнение (3) и интегрируя по 
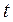от 
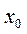до 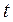, получим:
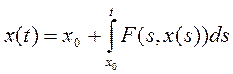(4).
Уравнения (3) и (4) – эквивалентны.
Рассмотрим уравнение: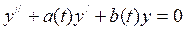 
с условиями 
, 
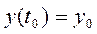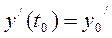(5)
Свести задачу Коши для данного уравнения к интегральному уравнению.
Обозначим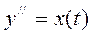 
, тогда 
.
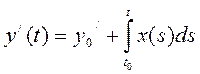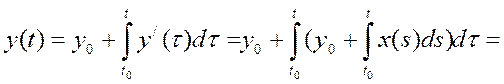
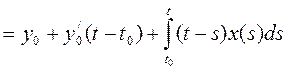
Итак, ,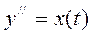 
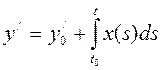
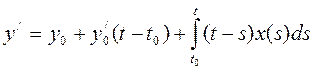(6)
Подставляя в исходное уравнение, получим:
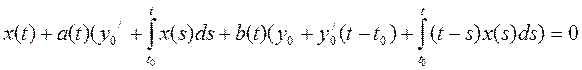(7)
или
,
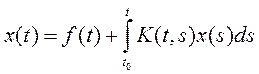где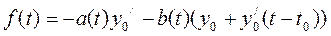 
,
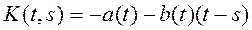(8).
Получим уравнение Вольтера или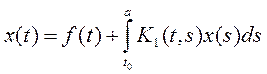 
– уравнение Фредгольма.
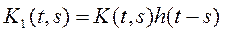, где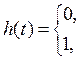 
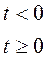
ЛЕКЦИЯ 13.
Теорема о существовании и единственности решения линейного интегрального уравнения Фредгольма 2-го рода с параметром.
Рассмотрим уравнение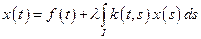 
(1)
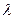– постоянное число, может быть комплексным.
; 
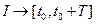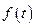и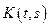 
- непрерывные функции и, следовательно, ограничены, т.е. 
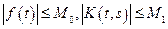. (2)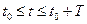 
, 
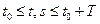
Будем доказывать существование и единственность решения уравнения (1), используя принцип сжатых изображений.
|
|
|
