Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже произошло.
Теорема умножения вероятностей
Зависимыми.
Зависимые и независимые события
Определение 2. Вероятность события B, вычисленная при условии, что событие A уже произошло, называется условной вероятностью события B и обозначается P(B/A).
Пример.___________________________________________________________
В урне 3 белых и 2 черных шара. Из урны дважды вынимают по одному шару, не возвращая обратно. Предположим, что при первом испытании был извлечен белый шар (событие A). Найдем вероятность появления белого шара при втором испытании (событие B). После первого испытания в урне осталось 4 шара, из них 2 белых. Значит, P(B/A)=2/4 =0,5. Если же при первом испытании был извлечен черный шар (событие C), то число белых шаров не изменилось, поэтому P(B/C)= 3/4=0,75.
Определение 3. Два события называются независимыми, если вероятность появления каждого из них не изменяется от того, появилось другое событие или нет. В противном случае события называются
Если событие A не зависит от события B, то его условная вероятность равна безусловной вероятности: P(A)= P(A/B).
Определение 4. Несколько событий называются независимыми в совокупности, если вероятность появления одного из них не изменяется при появлении каких-либо других оставшихся.
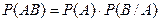 |
Следствие. 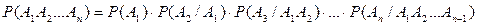
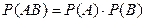 |
Следствие. 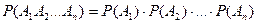
Примеры.__________________________________________________________
1. В ящике 25 деталей, из них 6 нестандартных. Найдем вероятность того, что две взятые наугад детали окажутся нестандартными.
Обозначим события: A − первая деталь окажется нестандартной, B− вторая деталь окажется нестандартной, AB − обе детали окажутся нестандартными. События A и B зависимы, поэтому
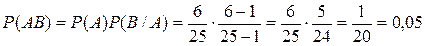 .
.
2. Произведен залп двух орудий по цели. Вероятность попадания из первого орудия (событие A) равна 0,8, из второго (событие B) − 0,75. Найдем вероятность события AB − совместного поражения цели двумя орудиями. Так как события A и B независимые, то
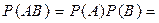 0,8∙0,75=0,6.
0,8∙0,75=0,6.
 2014-02-12
2014-02-12 1151
1151
