Классическое определение вероятности
Несколько событий, связанных с данным испытанием называются элементарными исходами испытания, если:
1) эти события образуют полную группу, т.е. при каждом осуществлении опыта наступает одно и только одно из них;
2) эти события являются равновозможными.
Те элементарные исходы, при которых событие A наступает, называются благоприятствующими событию A.
Пример.___________________________________________________________
Испытание − бросание игральной кости. События 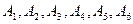 −всевозможные элементарные исходы испытания. Пусть событие A − на игральной кости выпало менее пяти очков. События
−всевозможные элементарные исходы испытания. Пусть событие A − на игральной кости выпало менее пяти очков. События 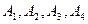 − элементарные исходы, благоприятствующие появлению события A.
− элементарные исходы, благоприятствующие появлению события A.
Определение. Вероятностью события A называется отношение числа m элементарных исходов, благоприятствующих событию A, к общему числу n всевозможных элементарных исходов испытания.
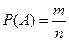
|
Примеры_________________________________________________________
1. Испытание − бросание монеты. Событие A− выпадение герба.
Так как n =2; m =1, то 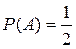 .
.
2. Испытание − бросание игральной кости. Событие A − на игральной кости выпадет менее 3 очков. Это испытание имеет следующие элементарные исходы: {1; 2; 3; 4; 5; 6}. Из них событию A благоприятствуют исходы {1; 2}. Поэтому n =6, m =2. Значит, 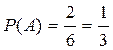 .
.
3. В урне 4 белых и 6 черных шаров. Наугад вынимают один шар.
Событие A− этот шар белый.Так как n =10, m =4, то P(A)=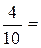 0,4.
0,4.
10 .Вероятность случайного события есть неотрицательное число,
заключенное между нулем и единицей: 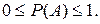
□ Число элементарных исходов, благоприятствующих наступлению
события, удовлетворяет неравенству 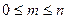 . Поэтому
. Поэтому 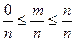 .
.
Значит, 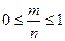 . Следовательно,
. Следовательно, 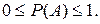 ■
■
 2014-02-12
2014-02-12 419
419








