 Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
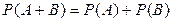 |
Следствие 1. 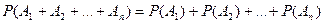 .
.
Следствие 2. Сумма вероятностей событий, образующих полную группу, равна единице.
 Вероятность суммы двух совместных событий
Вероятность суммы двух совместных событий 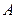 и
и 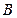 равна разности между единицей и вероятностью произведения противоположных событий
равна разности между единицей и вероятностью произведения противоположных событий 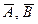 .
.
 |
□ Событие 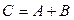 состоит в появлении хотя бы одного из событий
состоит в появлении хотя бы одного из событий 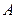 и
и 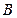 . Противоположное ему событие
. Противоположное ему событие 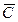 состоит в том, что не произойдет ни одно из событий
состоит в том, что не произойдет ни одно из событий 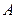 и
и 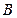 , т.е.
, т.е. 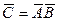 . Так как
. Так как 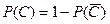 , то
, то
 ■
■
Следствие 1. 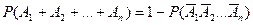 .
.
Следствие 2. Если события независимы в совокупности, то
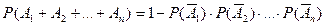 .
.
Если 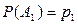 ,
, 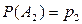 , …,
, …, 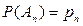 , то
, то
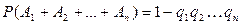 |
В частности, если 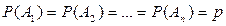 , то
, то
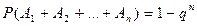 |
Примеры.__________________________________________________________
1. Вероятности банкротства для двух однотипных предприятий соответственно равны 0,1 и 0,2. Найдем вероятность банкротства хотя бы одного предприятия.
Обозначим события: 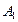 − банкротство первого предприятия,
− банкротство первого предприятия, 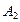 − банкротство второго предприятия, тогда
− банкротство второго предприятия, тогда 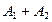 − банкротство хотя бы одного предприятия. События
− банкротство хотя бы одного предприятия. События 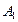 и
и 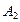 независимые.
независимые.
По условию 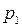 =0,1;
=0,1; 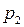 =0,2. Значит,
=0,2. Значит, 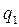 =1−0,1=0,9;
=1−0,1=0,9; 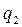 =1−0,2=0,8.
=1−0,2=0,8.
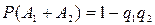 =1−0,9∙0,8=1−0,72=0,28.
=1−0,9∙0,8=1−0,72=0,28.
2. Вероятность попадания в цель при одном выстреле равна 0,6. Найдем вероятность хотя бы одного попадания при двух выстрелах.
Обозначим события: 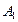 − попадание при первом выстреле,
− попадание при первом выстреле, 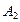 − попадание при втором выстреле. События
− попадание при втором выстреле. События 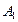 и
и 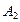 независимы.
независимы.
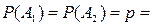 0,6;
0,6; 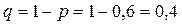 .
.
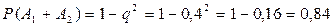 .
.
 2014-02-12
2014-02-12 1175
1175
