Для непрерывной случайной величины нельзя построить ряд распределения, так как она может принимать
бесконечное число значений из некоторого промежутка, кроме того, каждое отдельное значение обычно не
обладает никакой отличной от нуля вероятностью. Для непрерывной случайной величины нужен другой способ
задания закона распределения.
Общей формой задания закона распределения случайной величины является функция распределения вероятностей.
Определение 5. Функцией распределения вероятностей случайной величины 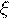 называется функция
называется функция 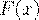 ,
,
определяющая вероятность того, что в результате испытания случайная величина 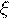 примет значение,
примет значение,
меньшее 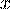 .
.
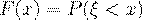 (1)
(1)
Геометрически равенство означает, что если случайная величина - это случайная точка на числовой оси, то
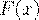 - это вероятность того, что в результате испытания случайная точка будет расположена левее точки
- это вероятность того, что в результате испытания случайная точка будет расположена левее точки 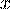 .
.
Функцию распределения еще принято называть интегральным законом распределения.
Из определения следует, что функция распределения существует и для дискретных случайных величин, и для
непрерывных. Для дискретных случайных величин формула (1) может быть записана следующим образом:
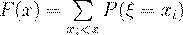 (2)
(2)
Свойства функции распределения.
1. 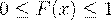
2. 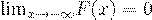
3. 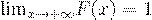
4. 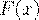 - неубывающая функция, то есть если
- неубывающая функция, то есть если 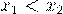 , то
, то 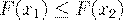 .
.
С помощью функции распределения можно найти вероятность попадания случайной величины на некоторый
промежуток по формуле:
 (3)
(3)
Так как  , то формула (3) верна
, то формула (3) верна
для всех этих случаев.
Пример 6. По мишени производится 3 выстрела. Вероятность попадания при одном выстреле 0,7.
Найти функцию распределения вероятностей случайной величины 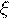 - числа попаданий при трех выстрелах.
- числа попаданий при трех выстрелах.
Решение. В примере 5 для данной случайной величины был получен ряд распределения:
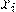 | ||||
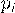 | 0,027 | 0,189 | 0,441 | 0,343 |
Используя формулу (2), найдем функцию распределения:
1. если 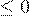 , то
, то 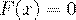 ;
;
2. если 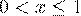 , то
, то  ;
;
3. если 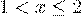 , то
, то 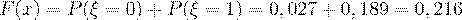 ;
;
4. если 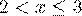 , то
, то 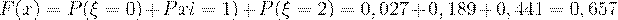 ;
;
5. если 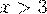 , то
, то 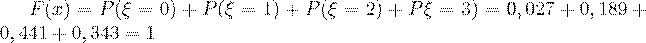 .
.
Итак, функция распределения аналитически может быть записана так:
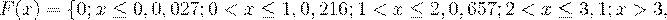
Теперь построим график этой функции.
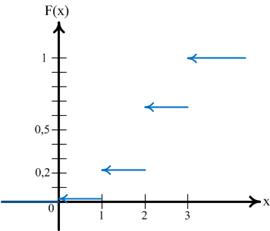
Рис.2
То есть функция распределения для дискретной случайной величины является кусочно-постоянной функцией,
имеющей конечное число точек разрыва 1-го рода.
Функция распределения непрерывной случайной величины является непрерывной функцией.
Пример 7. Дана функция распределения вероятностей непрерывной случайной величины 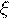 :
:
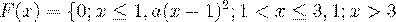
Найти 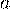 , построить график функции распределения, вычислить вероятность того, что в результате испытания
, построить график функции распределения, вычислить вероятность того, что в результате испытания
случайная величина 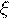 примет значение в интервале (1;2).
примет значение в интервале (1;2).
Решение. Для нахождения 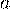 воспользуемся непрерывностью функции распределения:
воспользуемся непрерывностью функции распределения:
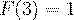 , поэтому
, поэтому 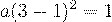 , следовательно
, следовательно  .
.
Построим график функции распределения:
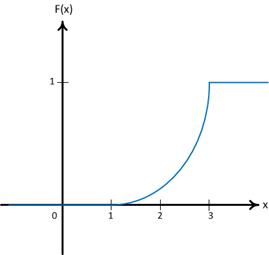
Рис.3
По формуле (3) находим: 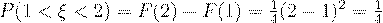 .
.
Вопрос. Если случайная величина 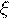 принимает значения, не большие 4, то
принимает значения, не большие 4, то 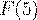 равно:
равно:
 2014-02-12
2014-02-12 7366
7366
