Определение 1. Пусть A =(aij) – матрица размера m×n над полем P, 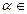 P. Произведением матрицы А на элемент
P. Произведением матрицы А на элемент 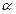 называется матрица С =(сij) размера m×n над полем P, где сij=
называется матрица С =(сij) размера m×n над полем P, где сij= 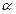 aij, j=
aij, j=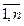 , i=
, i=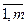 , и обозначается С=
, и обозначается С=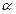 А.
А.
Определение 2. Пусть A =(aij) – матрица размера m×n над полем P, B =(bij) - матрица размера n×k над полем P. Произведением матриц А и В называется матрица С =(сij) размера m×k над полем P, в которой элемент сij равен скалярному произведению i- й строки матрицы А на j -й столбец матрицы B, т.е. сij=AiBj =(ai1 ... ain)⋅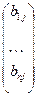 = ai1b1j+…+ainbnj =
= ai1b1j+…+ainbnj =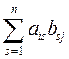 , i=
, i=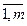 , j=
, j=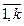 , и обозначается С=A⋅B.
, и обозначается С=A⋅B.
Лемма 1. Пусть А, В, С - матрицы над полем Р. Если существует произведение(АВ) С,то существует и произведение А (ВС),причем (АВ) С=А (ВС).
Доказательство. Пусть существует произведение (АВ) С. Тогда существуют матрицы АВ размера m×n и матрица С размера n×k. Это означает, что существуют матрицы А размера m×l и В размера l×n. Таким образом, существуют матрицы А, В и С соответственно размера m×l, l×n и n×k. Тогда существует произведение BC размера l×k и поэтому существует произведение А (ВС).
Покажем, что (AB) C=A (BC). Пусть (АВ) С= (xij), А (ВС) = (yij), i=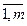 , j=
, j=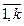 . Покажем, что xij=yij, i=
. Покажем, что xij=yij, i=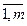 , j=
, j=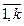 . Пусть A =(aip), B =(bps), С =(сsj), АВ=R= (ris), BC=T= (tpj), s=
. Пусть A =(aip), B =(bps), С =(сsj), АВ=R= (ris), BC=T= (tpj), s=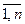 , p=
, p=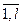 . Тогда
. Тогда
xij=RiCj= 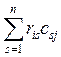 =
=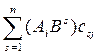 =
=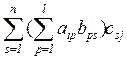 =
=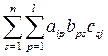 ,
,
yij=AiTj =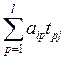 =
=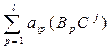 =
=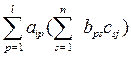 =
=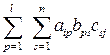 .
.
Таким образом, xij=yij, i=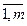 , j=
, j=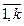 . Следовательно, (AB) C=A (BC). Лемма доказана.
. Следовательно, (AB) C=A (BC). Лемма доказана.
Лемма 2. Пусть A, B, C – матрицы над полем P следующих размеров: А и В – размера m×n, С – размера n×k. Тогда(А+В) С=АС+ВС.
Доказательство. Пусть (А+В) С= (xij), АС+ВС= (yij), i=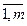 , j=
, j=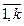 . Покажем, что xij=yij, i=
. Покажем, что xij=yij, i=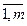 , j=
, j=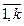 . Пусть A =(ais), B =(bis), С =(сsj), i=
. Пусть A =(ais), B =(bis), С =(сsj), i=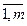 , s=
, s=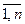 , j=
, j=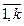 . Тогда
. Тогда
xij= (A+B) iСj= 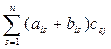 =
=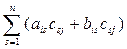 =
=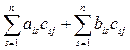 = AiCj+BiCj = yij.
= AiCj+BiCj = yij.
Следовательно, (А+В) С=АС+ВС. Лемма доказана.
Определение 3. Пусть A - матрица размера m×n над полем P. Транспонированием матрицы А называется операция замены в матрице А i -й строки на i -й столбец, i= 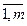 . Матрица, полученная в результате транспонирования матрицы A, называется матрицей, транспонированной к матрице A, и обозначается tA.
. Матрица, полученная в результате транспонирования матрицы A, называется матрицей, транспонированной к матрице A, и обозначается tA.
Пример 1. Если A =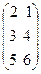 , то tА =
, то tА =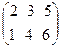 . Таким образом, если А – матрица размера m×n, то tА - матрица размера n×m.
. Таким образом, если А – матрица размера m×n, то tА - матрица размера n×m.
Лемма 3. Если произведение AB существует, то существует произведение tB tA, причем t (AB) = tB tA.
Лемма 4. Если А – матрица размера m × n над полем Р, то АЕn=EnA=A.
Доказательство осуществляется непосредственной проверкой.
Через Mn(P) обозначается множество всех квадратных матриц n -го порядка над полем P.
Замечание. Из свойств операций над матрицами следует, что Mn(P) - ассоциативное кольцо с единицей. Отметим, что умножение матриц некоммутативно (см. примеры на практических занятиях).
Лемма 5. Пусть А и В – матрицы над полем P, 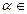 P. Тогда
P. Тогда 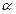 AB= (
AB= (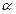 A) B=A (
A) B=A (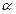 B).
B).
4. Перестановки n -й степени. Теорема о четности перестановки. Определители n -го порядка. Определители второго и третьего порядков.
Определение 1. Пусть М= { 1,2,…,n }. Перестановкой на множестве М или перестановкой n-й степени называется множество М с заданным расположением его элементов, и обозначается I= (i1i2…in), где i1,i2,..,in – попарно различные элементы из М.
Пример 1. Пусть М= { 1,2,3 }. Тогда перестановки на М имеют вид: I1= (132), I2= (231), I3= (123) и т.д.
Определение 2. Инверсией или беспорядком перестановки I называется любая пара символов перестановки I, в которой символ, стоящий левее, больше символа, стоящего правее.
Пример 2. В перестановке I2= (231) две инверсии: 31 и 21.
Через s (I) будем обозначать число всех инверсий перестановки I.
Определение 3. Перестановка I называется чётной, если s(I) – чётное число, в противном случае перестановка I называется нечётной.
В примере 2 перестановка I – чётная.
Через Sn обозначается множество всех перестановок n -ой степени. Можно доказать, что количество всех перестановок из n элементов равно n!=1×2×3×…×n. Например, из 3 элементов можно составить 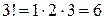 перестановок. Это будут 123, 132, 231, 321, 312, 231.
перестановок. Это будут 123, 132, 231, 321, 312, 231.
Определение 4. Транспозицией называется перемена местами 2-х элементов перестановки, когда остальные элементы остаются на месте.
Теорема 1. Транспозиция меняет четность перестановки. Другими словами, четность перестановки изменится, если в ней поменять местами два произвольных символа.
Пусть А =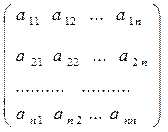 - матрица n -го порядка над полем Р.
- матрица n -го порядка над полем Р.
Из элементов матрицы А будем составлять всевозможные произведения, состоящие из n множителей, любые два различных из которых находятся в разных строках и разных столбцах. Таким, например, является произведение элементов, стоящих на главной диагонали: a11a22…ann. Все такие произведения можно получить по следующему правилу: выберем для произведения из первой строки матрицы А некоторый элемент 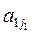 , затем вычеркнем первую строку и j1 -й столбец, и в полученной подматрице из первой строки выбираем некоторый элемент
, затем вычеркнем первую строку и j1 -й столбец, и в полученной подматрице из первой строки выбираем некоторый элемент 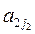 и т.д. Через конечное число шагов получим произведение вида:
и т.д. Через конечное число шагов получим произведение вида: 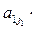
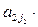 …
…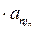 .
.
Так как j1,j2,…,jn – попарно различные элементы из множества М= { 1,2,…,n }, то вторые индексы в записанном произведении образуют перестановку I= (j1j2…jn).
Рассмотрим выражение вида: (-1) s (I) 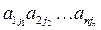 (1), где I= (j1j2…jn).
(1), где I= (j1j2…jn).
Выражений вида (1) можно образовать столько, сколько существует перестановок, составленных из вторых индексов, т.е. их будет n!.
Определение 5. Пусть А =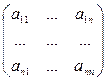 - матрица n -го порядка над полем Р. Определителем матрицы А (или, коротко, определителем n-го порядка) называется элемент
- матрица n -го порядка над полем Р. Определителем матрицы А (или, коротко, определителем n-го порядка) называется элемент 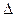 поля Р, равный
поля Р, равный 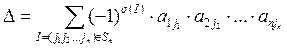 .
.
Используются следующие обозначения: 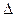 =
=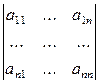 ,
, 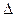 =| A |,
=| A |, 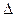 =| aij |, i =
=| aij |, i =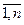 , j =
, j =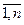 ,
,
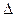 = det A.
= det A.
1) Пусть Δ – определитель 2-го порядка, т.е. Δ =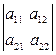 =
=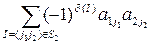 .
.
Так как I 1 = (12) и 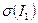 = 0, то получим Δ =
= 0, то получим Δ = 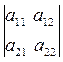 =
= 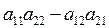 .
.
Таким образом, определитель 2-го порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.
2) Пусть Δ - определитель 3-го порядка: Δ = 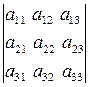 =
= 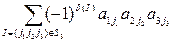 .
.
I 1 = (123) = 0 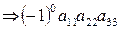 ; I 2 = (213) = 1
; I 2 = (213) = 1 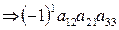 ;
;
I 3 = (312) = 2 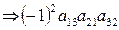 ; I 4 = (321) = 3
; I 4 = (321) = 3 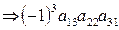 ;
;
I 5 = (132) = 1 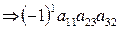 ;
;
I 6 = (231) = 2 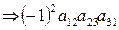 .
.
Следовательно,
Δ=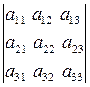 =
= 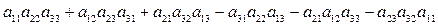 .
.
Таким образом, определитель 3-го порядка равен сумме шести слагаемых, три из которых со знаком +.
 2014-02-12
2014-02-12 1528
1528
