Конечная совокупность нескольких векторов с одинаковым числом координат называется системой векторов.
Пусть 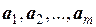 – система векторов в пространстве Rn,
– система векторов в пространстве Rn,
l1, …, l m – любые действительные числа. Составим вектор
b = 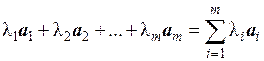 . (1.1)
. (1.1)
Определение. Любой вектор вида (1.1) называется линейной комбинацией векторов 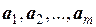 ; числа l1, …, l m называются коэффициентами этой линейной комбинации.
; числа l1, …, l m называются коэффициентами этой линейной комбинации.
Если 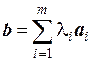 , то говорят, что вектор b линейно выражается через векторы
, то говорят, что вектор b линейно выражается через векторы 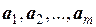 .
.
Пример. Составить линейную комбинацию векторов 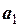 = (2; –1; 3),
= (2; –1; 3),
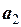 = (–2; 3; 1) и
= (–2; 3; 1) и 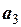 = (1; 1; 1) с коэффициентами l1 = 3, l2 = –1, l3 = 1.
= (1; 1; 1) с коэффициентами l1 = 3, l2 = –1, l3 = 1.
○ Линейной комбинацией векторов 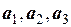 будет вектор
будет вектор
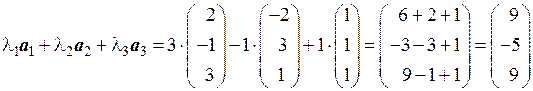 . ●
. ●
Определение. Система векторов 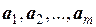 называется линейно зависимой, если существует набор чисел l1, …, l m, одновременно не равных нулю, такой, что линейная комбинация векторов системы
называется линейно зависимой, если существует набор чисел l1, …, l m, одновременно не равных нулю, такой, что линейная комбинация векторов системы 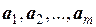 с коэффициентами l1, …, l m равна нулевому вектору.
с коэффициентами l1, …, l m равна нулевому вектору.
Таким образом, система 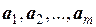 линейно зависима, если существует набор коэффициентов l1, …, l m,
линейно зависима, если существует набор коэффициентов l1, …, l m, 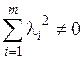 , такой, что
, такой, что
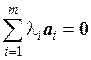 . (1.2)
. (1.2)
Если же равенство (1.2) справедливо только в том случае, когда все коэффициенты l1, …, l m равны нулю, 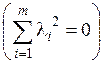 , то система векторов
, то система векторов 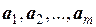 называется линейно независимой.
называется линейно независимой.
Примеры.
1. Рассмотрим систему векторов 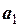 =(2;0;0),
=(2;0;0), 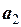 =(0;1;–1),
=(0;1;–1), 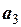 =(0;–2;2).
=(0;–2;2).
Составим линейную комбинацию этих векторов.
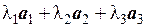 =
=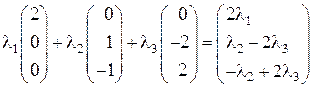 .
.
Эта линейная комбинация обращается в нулевой вектор при l1 = 0, 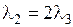 . При этом l3 может принимать любые значения, в том числе и ненулевые. Например, набор коэффициентов l1 = 0,
. При этом l3 может принимать любые значения, в том числе и ненулевые. Например, набор коэффициентов l1 = 0, 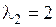 ,
, 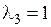 , среди которых есть и отличные от нуля, обращает линейную комбинацию векторов в нулевой вектор. Значит, данная система векторов
, среди которых есть и отличные от нуля, обращает линейную комбинацию векторов в нулевой вектор. Значит, данная система векторов 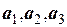 линейно зависима.
линейно зависима.
Замечание. Справедливость равенства 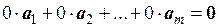 не означает еще линейной независимости системы векторов, так как если l1 = 0, l2 = 0, …, l m = 0, то линейная комбинация системы векторов
не означает еще линейной независимости системы векторов, так как если l1 = 0, l2 = 0, …, l m = 0, то линейная комбинация системы векторов 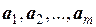 с такими коэффициентами равна нулевому вектору независимо от того, является ли эта система линейно зависимой или независимой. В частности, в приведенном выше примере при значениях коэффициентов
с такими коэффициентами равна нулевому вектору независимо от того, является ли эта система линейно зависимой или независимой. В частности, в приведенном выше примере при значениях коэффициентов 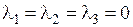 линейная комбинация векторов обращается в нулевой вектор. Однако, как мы выяснили, эта система линейно зависима, так как существуют и ненулевые наборы коэффициентов, при которых данная линейная комбинация обращается в нулевой вектор: 0× a 1+2× a 2+1× a 3 = 0.
линейная комбинация векторов обращается в нулевой вектор. Однако, как мы выяснили, эта система линейно зависима, так как существуют и ненулевые наборы коэффициентов, при которых данная линейная комбинация обращается в нулевой вектор: 0× a 1+2× a 2+1× a 3 = 0.
2. Покажем, что векторы a 1 = (2;0;0), a 2 = (0;1;2), a 3 = (0;0;–3) линейно независимы. Составим линейную комбинацию этих векторов и приравняем ее к нулевому вектору.
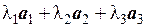 =
=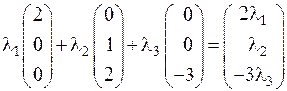 ,
, 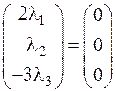 .
.
Последнее равенство верно только при 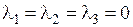 , что и означает линейную независимость векторов
, что и означает линейную независимость векторов 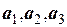 .
.
 2014-02-12
2014-02-12 490
490








