Понятие об n-мерном пространстве

Векторы

В аналитической геометрии вектором называется направленный отрезок, соединяющий две заданные точки – начало и конец вектора. Для геометрических векторов определены операции сложения векторов и умножения вектора на действительное число: сложение векторов определяется по правилу ²многоугольников²; при умножении вектора на действительное число k длина этого вектора умножается на 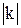, а направление вектора при k>0 остается прежним, а при k<0 меняется на противоположное. Эти операции называются линейными операциями над векторами.

Расширим понятие вектора. Будем рассматривать множества объектов любой природы, для элементов которых каким-либо способом определены операции сложения элементов и операции умножения элементов на действительное число, причем указанные операции обладают теми же свойствами, что и соответствующие операции над геометрическими векторами. Такие множества, называемые линейными (векторными) пространствами над множеством действительных чисел, обладают целым рядом общих свойств, которые мы теперь и будем рассматривать.

Определение линейного пространства. Множество R элементов 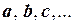любой природы называется линейным пространством, если выполнены следующие три требования:

I. Имеется правило, посредством которого любым двум элементам 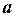и 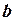множества R ставится в соответствие третий элемент 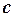этого множества, называемый суммой элементов 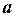и и 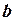обозначаемый символом .

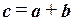II. Имеется правило, посредством которого любому элементу 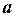множества R и любому вещественному числу 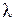ставится в соответствие элемент 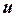этого множества, называемый произведением элемента 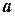на число 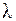и обозначаемый символом 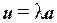или .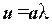

III. Указанные два правила подчинены следующим восьми аксиомам:

1°. 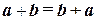(переместительное свойство суммы);

2°. 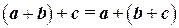(сочетательное свойство суммы);

3°. существует нулевой элемент 0 такой, что 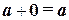для любого элемента 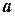(особая роль нулевого элемента);

4°. для каждого элемента 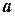существует противоположный элемент (–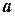) такой, что ;

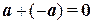5°. 1×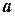=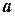для любого вектора 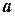(особая роль числового множителя 1);

6°. 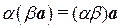(сочетательное относительно числового множителя свойство);

7°. 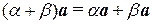(распределительное относительно суммы числовых множителей свойство);

8°. 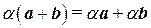(распределительное относительно суммы элементов свойство).

Следует заметить, что при введении понятия линейного пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов и произведения элемента на число (важно лишь, чтобы эти правила удовлетворяли восьми аксиомам, сформулированным в данном выше определении).

Примеры

1. Рассмотрим множество всех векторов в трехмерном пространстве.

Операции сложения векторов и умножения этих векторов на действительные числа определим так, как это было сделано в геометрии. В курсе геометрии установлена справедливость свойств
1°–8°. Таким образом, множество всех векторов в пространстве с определенными как в геометрии операциями сложения векторов и умножения их на число представляет собой векторное пространство, которое будем обозначать R³. Аналогичные множества векторов на плоскости и на прямой также являются векторными пространствами и обозначаются R² и R¹ соответственно.

2. Рассмотрим множество {х} всех положительных действительных чисел. Определим сумму двух элементов x и y этого множества как произведение действительных чисел x и y (понимаемое в обычном в теории действительных чисел смысле). Произведение элемента x множества {х} на действительное число l определим как возведение положительного действительного числа x в степень l. Нулевым элементом множества {х} будет являться действительное число 1, а противоположным (для данного элемента х) элементом будет являться действительное число 1/х.

Убедимся в справедливости всех аксиом 1°– 8°. Справедливость аксиом 1° и 2° вытекает из переместительного и сочетательного свойств произведения действительных чисел; справедливость аксиом 3° и 4° вытекает из элементарных равенств 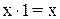, 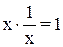(для любого действительного х > 0); аксиома 5° эквивалентна равенству 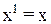; аксиомы 6° и 7° справедливы в силу того, что для любого х > 0 и любых действительных a и b имеют место соотношения 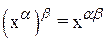, 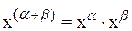; наконец, справедливость аксиомы 8° следует из того, что для любых положительных x и y и для любого действительного l имеет место равенство 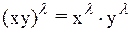. Итак, мы убедились, что множество {х} с так определенными операциями сложения элементов и умножения их на числа является линейным пространством.

3. Множество всех алгебраических многочленов относительно х вида 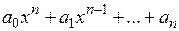(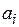– произвольные действительные числа), степень которых не превышает натурального числа n, с операциями, определенными обычными правилами математического анализа, является линейным пространством (проверьте самостоятельно).

Замечание. Множество всех многочленов степени, точно равной натуральному числу n, не является линейным пространством, так как сумма двух таких многочленов может оказаться многочленом степени ниже n.

4. Множество всех действительных чисел с обычными правилами сложения и умножения на число образует векторное пространство, так как сумма действительных чисел есть действительное число и при умножении действительного числа на любое действительное число снова получится действительное число; при этом справедливость аксиом 1°–8° очевидна.

5. Множество всех целых чисел не образует линейное пространство, так как, например, при умножении целых чисел на рациональные числа 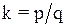, где p, q – произвольные целые числа, получаются рациональные числа, но не обязательно целые.

6. Все геометрические векторы пространства R², имеющие общее начало в начале координат и расположенные в I октанте, также не образуют линейное пространство, так как противоположные векторы расположены не в I октанте.

Определение. n-мерным вектором называется упорядоченная совокупность n действительных чисел 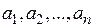, записываемая в виде: a = ().

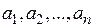В некоторых случаях n-мерный вектор удобно записывать в виде вектор-столбца 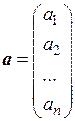. Числа 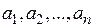называются координатами вектора, а число n (количество координат) называется размерностью этого вектора.

Определим линейные операции над n-мерными векторами.

Два n-мерных вектора с одинаковым числом координат 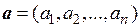и 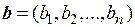считаются равными тогда и только тогда, когда равны их соответствующие координаты, а именно:

а = b Û .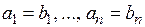

Следовательно, равенство двух векторов равносильно n равенствам соответствующих пар координат.

Суммой двух n-мерных векторов a и b называется вектор 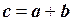, координаты которого равны суммам соответствующих координат слагаемых векторов, т.е. .

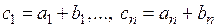Произведением вектора a на действительное число k называется вектор u, координаты которого равны произведению числа k на соответствующие координаты вектора a, т.е. .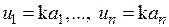

Вектор, каждая координата которого равна нулю, называется нулевым вектором и обозначается 0 = (0,0,…,0). Из определения операции сложения векторов следует, что для любого вектора a справедливо равенство 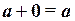. Равенство 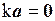верно тогда, когда 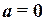, или k = 0, или 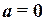и k = 0.

Вектор (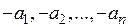) называется противоположным вектору
a = (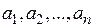) и обозначается (– a).

Легко проверить, что определенные таким образом линейные операции над n-мерными векторами обладают свойствами 1°–8°, рассматриваемыми как аксиомы, значит, множество всех n-мерных векторов является векторным (линейным) пространством. Будем обозначать это пространство Rⁿ.

Непосредственный геометрический смысл имеют только пространства R¹, R², R³(множество векторов на прямой, на плоскости и в пространстве, соответственно). Пространство Rⁿпри n>3 – чисто математический объект. Этот объект очень удобен для описания реальных процессов, в том числе экономических.

Пример. Даны векторы 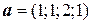и (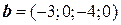. Найти вектор .

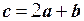[1]○ Выполним операции умножения вектора a на число 2 и суммирования векторов 2 a и b в координатной форме:

.

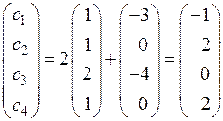Таким образом, координаты вектора с = (–1;2;0;2). ●

Векторы 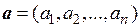и 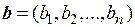называются коллинеарными, если найдется действительное число k такое, что k a = b или a = k b.

Если один из векторов a или b равен нулю, то такие векторы заведомо коллинеарны: если, например, a = 0, то имеем a = 0× b.

Очевидно, условие коллинеарности векторов означает пропорциональность соответствующих координат этих векторов, т.е. векторы a и b коллинеарны тогда и только тогда, когда найдется 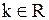такое, что справедливы равенства

.

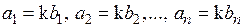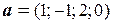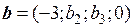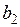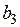Пример. Даны векторы и . При каких значениях и векторы a и b коллинеарны?

○ Векторы a и b коллинеарны, если пропорциональны их соответствующие координаты, т.е.

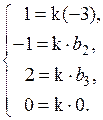
Из первого равенства имеем k=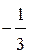, тогда 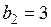, 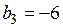; последнее равенство справедливо при любом действительном значении k. Следовательно, 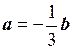и векторы a = 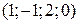и b = (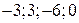) коллинеарны. ●