1°. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
□ 1. Пусть система, состоящая из одного вектора a 1, линейно зависима. Составим линейную комбинацию:
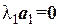 (1.3)
(1.3)
l1 ¹ 0 в силу линейной зависимости системы. По определению операции произведения вектора на действительное число векторное равенство (1.3) означает, что каждая координата вектора a 1 равна нулю, то есть вектор a 1 – нулевой вектор, a 1 = 0.
2. Пусть теперь a 1 = 0. Составим линейную комбинацию: l1 a 1 = 0. Это равенство выполняется при любом значении l1, в том числе и при l1 ¹ 0, а это означает, что система, состоящая из одного вектора a 1 линейно зависима. ■
2°. Система векторов, содержащая нулевой вектор, линейно зависима.
□ Пусть система векторов a 1,…, a k,…, a m содержит нулевой вектор, например, a k =0. Составим линейную комбинацию:
l1 a 1+…+l k a k + …+ l m a m = 0. (1.4)
Положим l1=0,…, l k –1=0, l k ¹0, l k +1=0,…, l m =0. Тогда равенство (1.4) справедливо и при этом 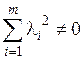 , значит, система a 1,…, a k,…, a m линейно зависима. ■
, значит, система a 1,…, a k,…, a m линейно зависима. ■
3°. Система векторов, состоящая более чем из одного вектора, линейно зависима тогда и только тогда, когда один вектор является линейной комбинацией остальных векторов системы.
□ 1. Пусть система векторов a 1,…, a k,…, a m линейно зависима. Тогда справедливо равенство: 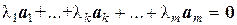 , причем
, причем 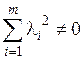 . Пусть l k ¹ 0. Поделим обе части равенства на l k и выразим вектор a k:
. Пусть l k ¹ 0. Поделим обе части равенства на l k и выразим вектор a k:
a k = –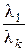 a 1 – …–
a 1 – …–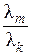 a m, то есть вектор a k является линейной комбинацией остальных векторов системы.
a m, то есть вектор a k является линейной комбинацией остальных векторов системы.
2. Пусть вектор a k является линейной комбинацией остальных векторов системы, то есть a k =l1 a 1 +…+l m a m. Тогда
– a k +l1 a 1 +…+l m a m = 0,
при этом l k = –1 ¹ 0; значит, система a 1,…, a k,…, a m линейно зависима.■
4°. Если часть системы векторов линейно зависима, то линейно зависима и вся система.
5°. Если система векторов линейно независима, то линейно независима любая ее подсистема.
Свойства 4° и 5° докажите самостоятельно.
6°. Если система a 1,…, a m линейно независима, а система
a 1, …, a m, a m +1 – линейно зависима, то вектор a m +1 является линейной комбинацией остальных векторов системы a 1,…, a m: a m +1 =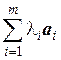 .
.
□ Так как система a 1,…, a m, a m +1 – линейно зависима, то справедливы равенства:
l1 a 1+…+l m a m +l m +1 a m +1= 0 (1.5)
при условии, что 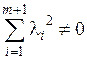 .
.
Если l m +1 = 0, то из равенства (1.5) следует, что l1 a 1+…+l m a m = 0, причем в силу линейной независимости системы a 1,…, a m последнее равенство справедливо только если все коэффициенты равны нулю, т.е. 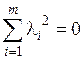 . Но тогда
. Но тогда 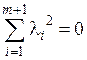 , что противоречит условию, следовательно, l m +1¹0. Тогда из равенства (1.5) имеем:
, что противоречит условию, следовательно, l m +1¹0. Тогда из равенства (1.5) имеем:
–l m +1 a m +1=l1 a 1+…+l m a m,
или 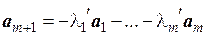 ,
,
где 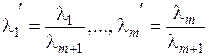 , что и требовалось доказать. ■
, что и требовалось доказать. ■
Рассмотрим некоторые частные случаи систем векторов, в которых вопрос о линейной зависимости решается просто.
1. Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда векторы коллинеарны.
□ 1. Пусть система, состоящая из векторов a 1 и a 2, линейно зависима. Если хотя бы один из векторов системы нулевой, то векторы коллинеарны. Пусть теперь оба вектора ненулевые. Так как система
a 1, a 2 линейно зависима, в равенстве l1 a 1+l2 a 2 = 0 хотя бы один из коэффициентов l1, l2 не равен нулю. Пусть l1 ¹ 0; тогда a 1 =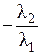 a 2, или a 1 = k ×a 2, где k =
a 2, или a 1 = k ×a 2, где k =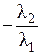 – некоторое число, значит, векторы a 1 и a 2 коллинеарны.
– некоторое число, значит, векторы a 1 и a 2 коллинеарны.
2. Пусть теперь векторы a 1 и a 2 коллинеарны. Если хотя бы один из этих векторов нулевой, то система a 1, a 2 линейно зависима (по свойству 2°). Пусть оба вектора ненулевые. Так как a 1 и a 2 коллинеарны, то найдется число k такое, что a 1 = k× a 2. Тогда
a 1– k× a 2 = 0, значит, система векторов a 1, a 2 линейно зависима (l1 ¹ 0). ■
Трехмерные векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости.
2. Система, состоящая из трех ненулевых трехмерных векторов a 1, a 2, a 3, линейно зависима тогда и только тогда, когда векторы компланарны.
□ 1. Пусть система a 1, a 2, a 3 линейно зависима. Тогда по свойству 3° линейной зависимости векторов один из векторов системы является линейной комбинацией остальных, например, a 1=k2 a 2+k3 a 3. Геометрически это соотношение означает, что вектор a 1 является диагональю параллелограмма, построенного на векторах k2 a 2 и k3 a 3, т.е. векторы a 1, a 2, a 3 лежат в одной плоскости (компланарны).
2. Пусть теперь векторы a 1, a 2, a 3 лежат в одной плоскости. Возможны два случая: 1) хотя бы два из трех векторов a 1, a 2, a 3 коллинеарны, т.е. лежат на одной прямой (или на параллельных прямых); 2) векторы a 1, a 2, a 3 попарно не коллинеарны, т.е. никакие два из них не лежат на одной прямой.
В первом случае пусть, например, векторы a 1 и a 2 коллинеарны. Тогда по доказанному выше система a 1, a 2 линейно зависима, откуда по свойству 4° линейной зависимости следует, что система a 1, a 2, a 3 линейно зависима.
Во втором случае a 1 и a 2 не лежат на одной прямой. Проведем через конец вектора a 3 прямые, параллельные векторам a 1 и a 2 (рис.1.1). Тогда вектор a 3 является диагональю параллелограмма, построенного на векторах a 1¢ и a 2¢, т.е. a 3= a 1¢ + a 2¢. Так как векторы a 1 и a 1¢, а также a 2 и a 2¢ коллинеарны, то a 1¢= k1 a 1, a 2¢=k2 a 2, значит, a 3= k1 a 1 + k2 a 2 и система a 1, a 2, a 3 линейно зависима.

Рис. 1.1
Итак, доказано, что в каждом из рассмотренных случаев система векторов a 1, a 2, a 3 линейно зависима. ■
Рассмотрим систему векторов
a 1=(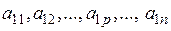 ),
),
a 2=(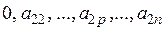 ), (1.6)
), (1.6)
…….…………..………,
a р =(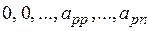 ).
).
Здесь 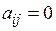 , если
, если 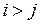 и
и 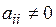 ,
, 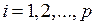 . Системы векторов вида (1.6) будем называть диагональными. Очевидно, для диагональной системы всегда
. Системы векторов вида (1.6) будем называть диагональными. Очевидно, для диагональной системы всегда 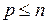 , т.е. число векторов не превышает числа координат в каждом отдельном векторе.
, т.е. число векторов не превышает числа координат в каждом отдельном векторе.
3. Диагональная система векторов линейно независима.
□ Составим линейную комбинацию векторов системы (1.6):
b = l1 a 1+…+l р a р.
Выясним, в каком случае вектор b равен 0, т.е. когда l1 a 1+…+l р a р = 0. Последнее векторное равенство равносильно n равенствам координат:
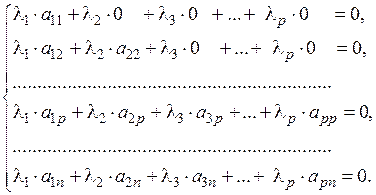 (1.7)
(1.7)
Так как 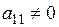 , то из первого уравнения имеем
, то из первого уравнения имеем 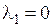 . Тогда из второго уравнения получим
. Тогда из второго уравнения получим 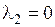 (
(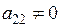 ) и т.д. Подставляя в
) и т.д. Подставляя в 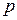 -ое уравнение полученные выше значения
-ое уравнение полученные выше значения 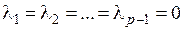 при условии
при условии 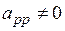 получаем
получаем 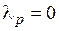 . Таким образом, равенство l1 a 1+…+l р a р =0 возможно лишь при условии
. Таким образом, равенство l1 a 1+…+l р a р =0 возможно лишь при условии 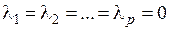 , что и означает линейную независимость системы (1.6). ■
, что и означает линейную независимость системы (1.6). ■
Из доказанного следует, что в пространстве Rnсуществует линейно независимая система, содержащая ровно n векторов. Примером такой системы может служить система, состоящая из векторов
е 1=(1;0;…;0), е 2=(0;1;…0),…, 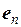 =(0;0;…;1), (1.8)
=(0;0;…;1), (1.8)
которая является частным случаем диагональной системы (1.6).
Естественно, возникает вопрос: можно ли в пространстве Rn построить систему, состоящую более чем из n линейно независимых векторов? Ответ на этот вопрос дает следующая теорема, которую мы принимаем без доказательства.
Теорема 1.1. В пространстве Rn любая система, содержащая m векторов, линейно зависима при m > n.
Итак, максимальное число содержащихся в пространстве Rn линейно независимых векторов равно n и любой (n+1) вектор этого пространства линейно выражается через указанные n векторов.
Рассмотрим систему векторов a 1, a 2,…, a k.
Определение. Базисом системы векторов a 1, a 2,…, a k называется частичный набор векторов этой системы (подсистема), удовлетворяющий двум условиям:
1) векторы этого набора линейно независимы;
2) любой вектор системы a 1, a 2,…, a k линейно выражается через векторы этого набора.
Векторы, входящие в базис, называются базисными векторами.
Рангом системы векторов называется число векторов ее базиса. Если ранг системы векторов меньше числа k ее векторов, то система может иметь несколько базисов. Справедлива теорема, утверждающая, что все базисы данной системы векторов содержат одно и то же число векторов.
Пример. В системе векторов a 1=(–1;1;0), a 2=(2;0;1), a 3=(–3;3;0) найти все возможные базисы.
○ Вектор a 3 коллинеарен вектору a 1, значит, система векторов a 1, a 2, a 3 линейно зависима и ее ранг не превосходит двух. Так как векторы a 1 и a 2 неколлинеарны, а значит линейно независимы, то их можно взять в качестве базисных векторов. За базисные векторы можно также принять неколлинеарные векторы a 2 и a 3. Итак, в данной системе векторов существует два базиса: (a 1, a 2) и (a 2, a 3). ●
Рассмотрим простейшие свойства ранга системы векторов.
1°. Ранг системы векторов не превосходит числа векторов системы.
2°. Если система векторов линейно зависима, то ранг системы меньше числа векторов системы.
3°. Если система векторов линейно независима, то ранг системы равен числу векторов системы.
Понятие базиса можно распространить на векторное пространство Rn, которое является бесконечной совокупностью n-мерных векторов.
Определение. Система векторов называется базисом пространства Rn, если:
1) эта система векторов линейно независима;
2) любой вектор из Rnлинейно выражается через векторы данной системы.
В пространстве Rnсуществует бесчисленное множество базисов. При этом справедлива следующая теорема:
Теорема 1.2. Линейно независимая система векторов в Rn является базисом тогда и только тогда, когда число векторов этой системы
равно n.
Число n определяет размерность пространства.
Примеры.
1. Базисом пространства R1 является любой ненулевой вектор a 1, лежащий на оси Ох, так как: 1) система, состоящая из одного ненулевого вектора, линейно независима; 2) любой другой вектор этого пространства по свойству операции умножения вектора на число линейно выражается через этот вектор: a 2 = k a 1.
2. Базис пространства R2 образуют любые два неколлинеарных вектора, так как они линейно независимы.
3. Базис пространства R3 образуют любые три свободные некомпланарные векторы, так как они линейно независимы.
4. Диагональная система векторов (1.6) при р = n является базисом пространства Rn, так как состоит из n линейно независимых векторов.
Теорема 1.3. Любой вектор пространства Rnможно представить в виде линейной комбинации базисных векторов, притом единственным образом.
□ Пусть векторы a 1, a 2,…, a n образуют базис пространства Rn. Тогда система a 1, a 2,…, a n, b линейно зависима и по свойству 6° вектор b является линейной комбинацией остальных векторов системы:
b =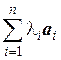 . То, что такое представление единственно, докажем методом от противного.
. То, что такое представление единственно, докажем методом от противного.
Предположим, что существуют два различных разложения вектора b по базису a 1, a 2,…, a n: b =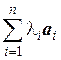 и b =
и b =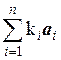 . Рассмотрим разность
. Рассмотрим разность 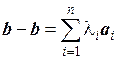 –
–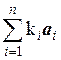 , или 0 =
, или 0 =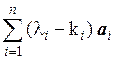 . Так как система a 1, a 2,…, a n образует базис пространства Rnи, значит, линейно независима, то из последнего равенства следует
. Так как система a 1, a 2,…, a n образует базис пространства Rnи, значит, линейно независима, то из последнего равенства следует
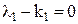 ,
, 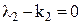 ,…,
,…, 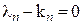 , или
, или 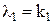 ,
, 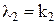 ,…,
,…, 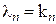 . Но это противоречит тому, что разложения
. Но это противоречит тому, что разложения 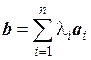 и b =
и b =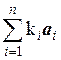 различны. ■
различны. ■
В силу доказанной теоремы любой вектор в пространстве Rnоднозначно определяется коэффициентами разложения вектора
по данному базису, т.е. упорядоченной совокупностью действительных чисел (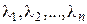 ). Таким образом, коэффициенты разложения вектора по данному базису являются координатами этого вектора в данном базисе. Из доказанной теоремы следует, что равные векторы имеют равные координаты.
). Таким образом, коэффициенты разложения вектора по данному базису являются координатами этого вектора в данном базисе. Из доказанной теоремы следует, что равные векторы имеют равные координаты.
При переходе к другому базису координаты вектора, вообще говоря, меняются. Пусть, например, координаты вектора b = (1;–3) определены в базисе е 1=(1;0), е 2=(0;1), т.е. b = е 1–3 е 2. Векторы a 1=(2;0), a 2=(–1;3) также образуют базис пространства R2. Координатами вектора b в базисе a 1, a 2 являются коэффициенты разложения этого вектора по базисным векторам.
b =l1 a 1+l2 a 2=l1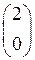 +l2
+l2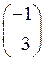 =
=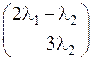 .
.
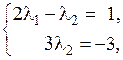
откуда 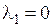 ,
, 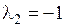 . Тогда
. Тогда 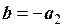 и координаты вектора b в базисе a 1, a 2 будут (0;–1).
и координаты вектора b в базисе a 1, a 2 будут (0;–1).
Если не указан базис пространства Rn, в котором задан вектор, мы будем полагать, что вектор задан в базисе
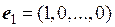 ,
,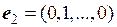 , …,
, …, 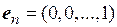 .
.
Пример. Найти разложение вектора b = 2 е 1– е 2+3 е 3 по векторам
a 1 = 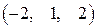 , a 2 =
, a 2 = 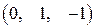 и a 3 =
и a 3 = 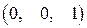 .
.
○ Векторы a 1, a 2, a 3 образуют диагональную систему векторов, значит, они линейно независимы. Число векторов системы n = 3 равно размерности пространства. Следовательно, по теореме 2.2 векторы
a 1, a 2, a 3 образуют базис пространства R3, и вектор b может быть разложен по этим векторам единственным образом. Составим линейную комбинацию
b = l1 a 1+ l2 a 2 + l3 a 3.
Это векторное равенство можно записать в координатной форме:
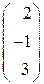 =l1
=l1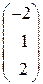 +l2
+l2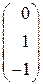 + l3
+ l3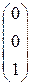 ,
,
или системой уравнений:
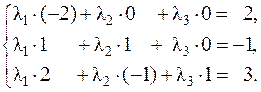
Из первого уравнения получим l1 = –1, тогда из второго уравнения l2 = 0, и из третьего – l3 = 5.
Таким образом, вектор b имеет координаты (–1; 0; 5) в
базисе a 1, a 2, a 3 или b = – a 1 +5 a 3. ●
Для нахождения координат вектора в другом базисе пространства Rn приходится решать систему n линейных уравнений относительно коэффициентов разложения вектора в этом базисе. В общем случае преобразованием координат вектора при переходе к другому базису мы будем заниматься в п. 4.
 2014-02-12
2014-02-12 2540
2540