Ортогональная система векторов

Определение. Векторы a и b называются ортогональными (перпендикулярными) друг другу, если их скалярное произведение равно нулю, т.е. a × b = 0.

Для ненулевых векторов a и b равенство нулю скалярного произведения означает, что cos j = 0, т.е. 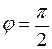. Нулевой вектор ортогонален любому вектору, т.к. a × 0 = 0.

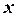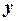Упражнение. Пусть и – ортогональные векторы. Тогда 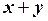естественно считать диагональю прямоугольника со сторонам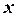и и 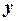. Докажите, что

,

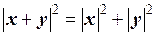т.е. квадрат длины диагонали прямоугольника равен сумме квадратов длин двух его непараллельных сторон (теорема Пифагора).

Определение. Система векторов a ₁,…, a _m называется ортогональной, если ортогональны любые два вектора этой системы.

Таким образом, для ортогональной системы векторов a ₁,…, a _m справедливо равенство: a _i × a _j = 0 при i ¹ j, i = 1,…, m; j = 1,…, m.

Теорема 1.5. Ортогональная система, состоящая из ненулевых векторов, линейно независима..

□ Доказательство проведем от противного. Предположим, что ортогональная система ненулевых векторов a ₁, …, a _m линейно зависима. Тогда

l₁ a ₁ + …+ l _m a _m = 0, при этом 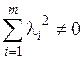. (1.15)

Пусть, например, l₁ ¹ 0. Домножим на a ₁ обе части равенства (1.15):

l₁ a ₁× a ₁+ …+ l _m a _m × a ₁ = 0.

Все слагаемые, кроме первого, равны нулю в силу ортогональности системы a ₁, …, a _m. Тогда l₁ a ₁× a ₁=0, откуда следует a ₁ = 0, что противоречит условию. Наше предположение оказалось неверным. Значит, ортогональная система ненулевых векторов линейно независима. ■

Имеет место следующая теорема.

Теорема 1.6. В пространстве Rⁿ всегда существует базис, состоящий из ортогональных векторов (ортогональный базис)
(без доказательства).

Ортогональные базисы удобны прежде всего тем, что коэффициенты разложения произвольного вектора по таким базисам определяются просто.

Пусть требуется найти разложение произвольного вектора b по ортогональному базису е ₁,…, е _n. Составим разложение этого вектора с неизвестными пока коэффициентами разложения по данному базису:

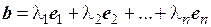(1.16)

Умножим обе части этого равенства скалярно на вектор e ₁. В силу аксиом 2° и 3° скалярного произведения векторов получим

.

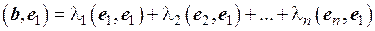Так как векторы базиса е ₁,…, е _n взаимно ортогональны, то все скалярные произведения векторов базиса, за исключением первого, равны нулю, т.е. коэффициент 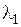определяется по формуле

.

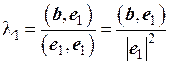Умножая поочередно равенство (1.16) на другие базисные векторы, мы получим простые формулы для вычисления коэффициентов разложения вектора b:

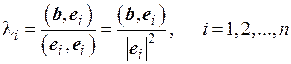. (1.17)

Формулы (1.17) имеют смысл, поскольку .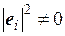

Определение. Вектор a называется нормированным (или единичным), если его длина равна 1, т.е. ( a, a )= 1.

Любой ненулевой вектор можно нормировать. Пусть a ¹ 0. Тогда 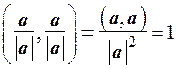, и вектор 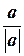есть нормированный вектор.

Определение. Система векторов е ₁,…, е _n называется ортонормированной, если она ортогональна и длина каждого вектора системы равна 1, т.е.

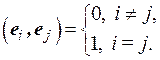(1.18)

Так как в пространстве Rⁿвсегда существует ортогональный базис и векторы этого базиса можно нормировать, то в Rⁿ всегда существует ортонормированный базис.

Примером ортонормированного базиса пространства Rⁿможет служить система векторов е ₁,=(1,0,…,0),…, е _n =(0,0,…,1) со скалярным произведением, определенным равенством (1.9). В ортонормированном базисе е ₁,=(1,0,…,0),…, е _n =(0,0,…,1) формулы (1.17) для определения координат разложения вектора b имеют наиболее простой вид:

, .

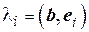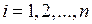Пусть a и b – два произвольных вектора пространства Rⁿ с ортонормированным базисом е ₁,=(1,0,…,0),…, е _n =(0,0,…,1). Обозначим координаты векторов a и b в базисе е ₁,…, е _n соответственно через a ₁,…, a _n и b ₁,…, b _n и найдем выражение скалярного произведения этих векторов через их координаты в данном базисе, т.е. предположим, что

, .

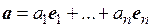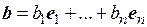Тогда

.

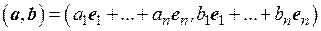Из последнего равенства в силу аксиом скалярного произведения и соотношений (1.18) получим

.

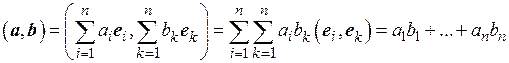Окончательно имеем

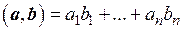. (1.19)

Таким образом, в ортонормированном базисе скалярное произведение двух любых векторов равно сумме произведений соответствующих координат этих векторов.

Рассмотрим теперь в n-мерном евклидовом пространстве Rⁿсовершенно произвольный (вообще говоря, не ортонормированный) базис 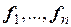и найдем выражение скалярного произведения двух произвольных векторов a и b через координаты этих векторов в указанном базисе.

Обозначим координаты векторов a и b в базисе 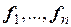соответственно через a ₁,…, a_n и b ₁,…, b_n, т.е. предположим, что , .

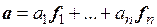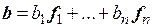Пользуясь аксиомами скалярного произведения, получим

=.

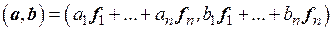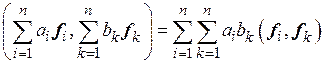Таким образом, в произвольном базисе 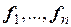скалярное произведение двух любых векторов 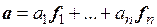, 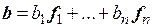определяется равенством

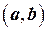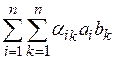=, (1.20)

где .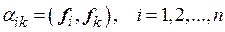

Последнее утверждение приводит к следующему результату: для того, чтобы в данном базисе f ₁,…, f _n евклидова пространства Rⁿскалярное произведение двух любых векторов было равно сумме произведений соответствующих координат этих векторов, необходимо и достаточно, чтобы базис f ₁,…, f _n был ортонормированным.

В самом деле, выражение (1.20) переходит в (1.19) тогда и только тогда, когда выполнены соотношения 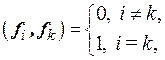устанавливающие ортонормированность базиса f ₁,…, f _n.