Теория линейных векторов и операторов квантовой механики

Дифференциальные выражения вида:

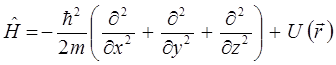
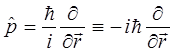
Представляют собой частный случай линейных операторов, а функции 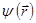- частный случай векторов, на которые действуют операторы.

Трёхмерный вектор 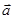однозначно задаётся тройкой компонент (проекций) вектора на три неэквивалентных направления в пространстве: 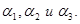Сумма двух векторов в пространстве 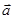и 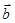- есть новый вектор, составленный из сумм одноимённых компонент 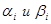, тогда соответственно:

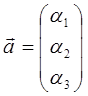
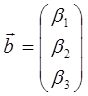
таким образом:

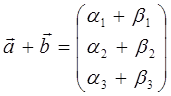
Умножение вектора 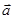на скаляр (число) 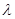, есть «растяжение» вектора 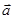в 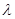раз и отвечает новому вектору вида:

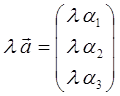
Для пары действительных векторов 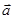и 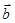вводится числовая характеристика – скалярное произведение. При скалярном перемножении двух векторов получают скаляр (число):

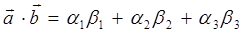
равное сумме произведений их проекций 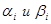. Модулем (длиной) вектора 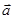называют выражение вида:

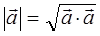
здесь:

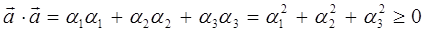
Во многих задачах неизбежен переход от вещественных (действительных) чисел к комплексным. Так некоторое число вида:

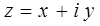
где 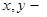любые действительные (вещественные) числа и 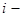мнимая единица.

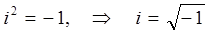
называется комплексным числом, где 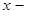действительная часть комплексного числ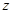а , а 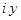- мнимая часть комплексного числа 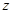. Если изобразить комплексное число в виде: 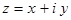, что отразится точкой на плоскости oxy, то абсциссой данной точки будет служить действительная, а ординатой – мнимая части комплексного числа 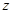. Поэтому ось абсцисс ox называется действительной осью, а ось ординат oy – мнимой осью; плоскость же называется комплексной плоскостью. Положение точки на комплексной плоскости задаётся радиус-вектором 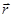, идущим из начала координат в указанную точку местонахождения рассматриваемого комплексного числа. Проекциями вектора 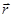на оси абсцисс и ординат являются соответственно действительная и мнимая части комплексного числа 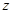, тогда очевидно: при y=0, комплексное число есть действительная величина, изображаемая точкой на действительной оси, т.е.

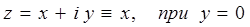
x=0, комплексное число есть мнимая величина, которой соответствует точка на мнимой оси, т.е.

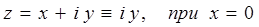
В теории комплексных чисел вводят понятие комплексного сопряжения, т.е. каждому комплексному числу 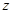, ставится в соответствие комплексно сопряжённая ему величина 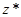, тогда, следовательно:

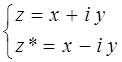
здесь:

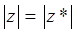
поскольку:

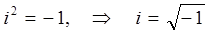
тогда будем иметь соответственно:

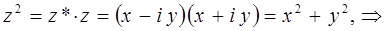
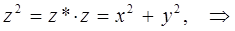
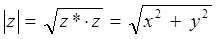
учитывая, что:

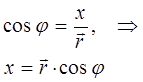
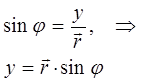
следовательно:

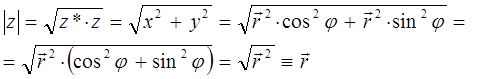
таким образом:

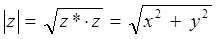
поскольку:

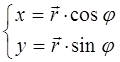
поэтому:

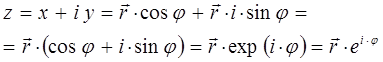
и аналогично:

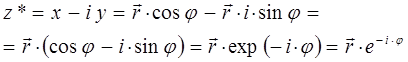
таким образом, в ходе проделанных выкладок приходим к выражениям вида:

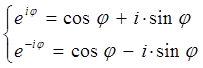
откуда следует, что:

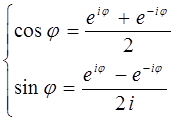
На основании приведенных выше выкладок, неотрицательность скалярного квадрата:

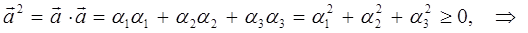
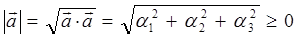
будет выполняться, очевидно, если приведенное выше выражение будет вычисляться по более общей формуле:

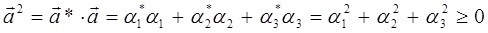
тогда:

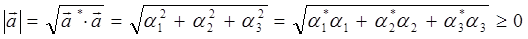
Подобным же образом уточняется скалярное произведение двух других

векторов 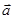и :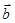

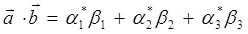
При работе с векторами в квантовой механике широко используются скобочные обозначения Дирака. Математически они компактны, удобны в обращении и легко запоминаются.

Векторы-столбцы (кет-векторы):

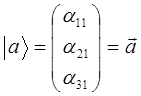
тогда:

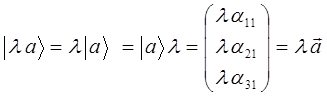
Векторы-строки (бра-векторы):

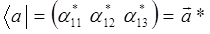
тогда:

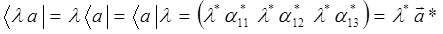
Смысл подобной символики становится понятным после записи скалярного произведения векторов 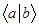. Пользуясь известным из теории матриц правилом умножения строки на столбец, согласно которому: «Операция умножения двух матриц имеет место только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы». Поскольку в нашем случае число столбцов бра-вектора 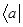равно числу столбцов кет-вектора , будем иметь соответственно:

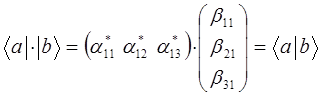
Для упрощения и большей наглядности, изменим обозначения матричных элементов (проекций векторов) соответствующих матриц, тогда будем иметь соответственно:

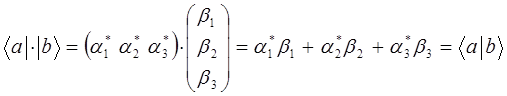
произведение, представленное полной скобкой Дирака «бракет», составленное из матричных элементов (проекций разложения соответствующих векторов) будет имеющее вид:

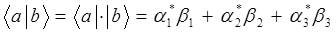
будет определяться, таким образом, как скалярное произведение бра-вектора 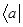на кет-вектор . В ряде случаев удобно разложить вектор характеризующий поле действительных (вещественных) чисел по базисному набору простейших (элементарных) векторов 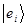, геометрическим образом которых являются декартовые единичные векторы – орты. Разложим кет-вектор по-базисному набору простейших (элементарных) векторов:

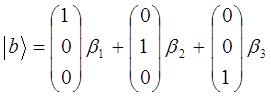
обозначив простейшие (базисные) вектора через 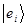, будем иметь соответственно:

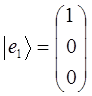
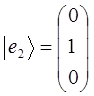
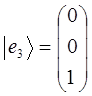
тогда, следовательно:

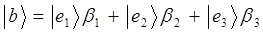
Полученное выше последнее выражение представляет собой разложение кет вектора по-базисному набору векторов: 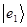, , 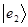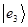. Каждый такой простейший (базисный) вектор 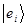нормирован и ортогонален или говоря об одновременной его нормированности и ортогональности, говорят, что он обладает свойством ортонормированности по-отношению ко всем другим векторам из рассматриваемого базисного набора, т.е.

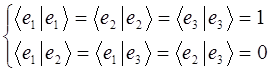
или, что то же самое:

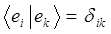
Достаточно очевидно, что:

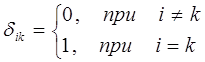
где 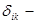символ Кронекера. Ортогональность векторов означает их линейную независимость, т.е. что векторы располагаются по-отношению друг ко другу под углом 90⁰ и ни один из векторов данного набора нельзя выразить через линейную комбинацию остальных 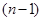векторов. Ортогональность волновых функций как линейных векторов – фундаментальное их свойство, следующее из более общего принципа суперпозиций. Линейная независимость векторов означает, что ни один из векторов рассматриваемого векторного пространства не сводится один к другому, и, следовательно, не является линейной комбинацией других векторов из данного базисного набора, не содержит в себе примеси любого другого из векторов. Учитывая, что норма вектора есть характеристика его длины (модуль вектора), а также что:

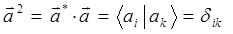
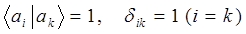
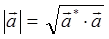
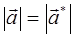
и кет-вектор соответствует волновой функци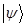и или 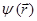, тогда свойство нормированности волновой функции 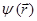можно интерпретировать как плотность вероятности микрочастицы, положение плотности, вероятности которой задаётся вектором 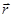, тогда соответственно будем иметь:

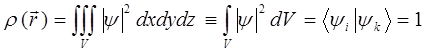
В различных задачах используют не трёхмерные, а многомерные (N-мерные) вектора. N-мерным кет-вектором называется упорядоченная совокупность N-комплексных чисел 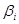(компонент вектора ), т.е.

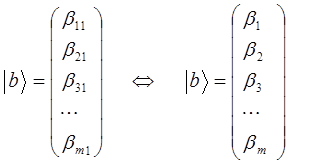
здесь m = 1, 2, 3, 4, … k. Множество таких многомерных векторов образую N-мерное векторное пространство 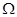. Для N-мерных векторов справедливы те же линейные операции, что и для уже рассмотренных выше трёхмерных векторов, тогда:

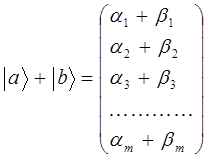
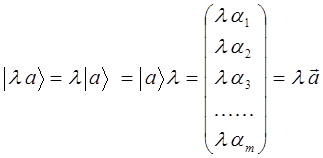
Пространство, образуемое многомерными векторами, называется также конечномерным. Наряду с пространством 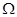кет-векторов , вводится комплексно сопряжённое ему пространство 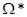образуемое полем N-мерных бра-векторов :

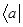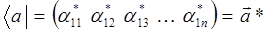
или меняя номера матричных элементов (из соображений удобства и наглядности), имеем соответственно:

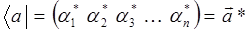
Как и в случае трёхмерных векторов, для многомерных бра-векторов имеем те же линейные операции:

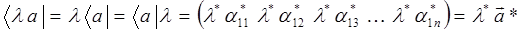
или после смены нумерации:

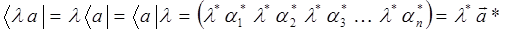
Тогда скалярное произведение многомерных векторов 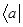и будет определяться соответственно выражением вида:

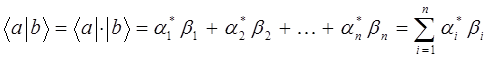
здесь: 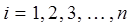. Таким образом, имеем соответственно:

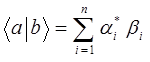
Используя приведенные выше рассуждения, можно сформулировать достаточно простые правила для скалярного произведения векторов 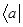и :

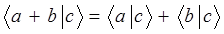
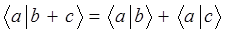
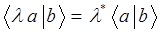
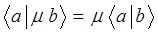
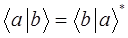
Многомерные векторы, как и трёхмерные, можно разложить по-базисному набору элементарных (простейших) векторов, т.е.

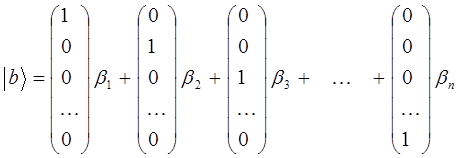
здесь:

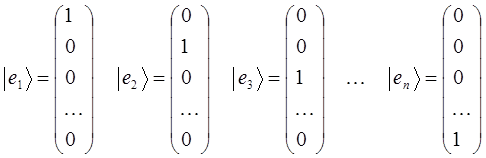
таким образом, имеем:

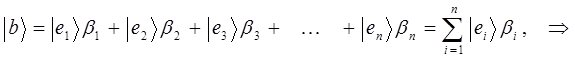
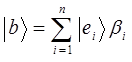
Последнее выражение представляет собой разложение кет-вектора по-базисному набору простейших (элементарных) векторов 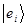. Базис представляет собой набор элементарных векторов, он обладает важным качеством – ортонормированностью. Это в свою очередь говорит о том, что он должен удовлетворять условиям вида:

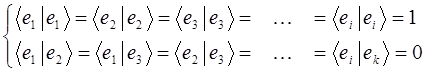
таким образом, имеем:

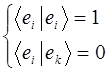
Данное утверждение удобней записывать, используя символ Кронекера :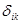

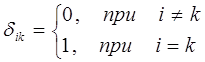
тогда соответственно:

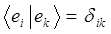
Всякий базис удовлетворяющий данным условиям, называется ортонормированным. В ортонормированном базисе, коэффициенты разложения 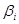вычисляются как скалярное произведение:

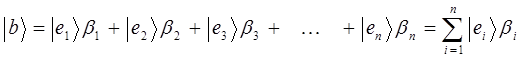
Таким образом, для случая многомерных векторов образующих конечномерное векторное пространство 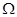, будем иметь:

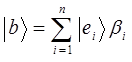
Умножая правую и левую части полученного выражения на базисный вектор вида 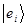и учитывая условия вида:

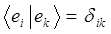
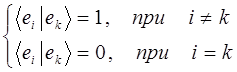
имеем соответственно:

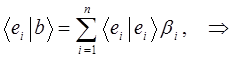
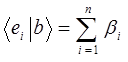
здесь:

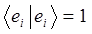
таким образом, для коэффициентов разложения (называемых также коэффициентами Фурье) 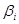приходим к выражению вида:

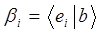
Выражая разложение по-базисному набору векторов через соответствующие коэффициенты Фурье 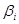, имеем соответственно:

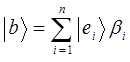
т.к. 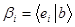, тогда, следовательно:

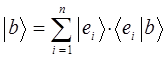
Отсюда следует, что если система векторов ортонормированна, то она служит базисом -векторного пространства. Покажем теперь, что множество функций можно воспринимать как векторное пространство бесконечного числа измерений. Такое пространство называется в квантовой механике функциональным, т.е. функциональное пространство – это тип векторного пространства, образованное множеством функций. Итак, пусть имеется множество функций одной переменной 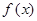на заданном интервале 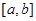. Разобьем интервал 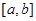на 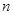частей длиной 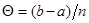, учтём также, что: .

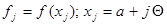Тогда всю совокупность действительных (вещественных) значений функции 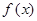можно представить кет-вектором:

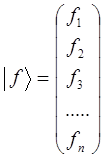
который при 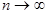даёт точное представление о функции 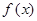и таким образом значение 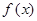в точке 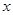оказывается одной из компонент функционального вектора 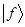. На основании представлений о функциональном пространстве и выражении функции 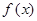как некоторого функционального кет-вектора 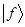, можно уточнить представления о скалярном произведении двух векторов. 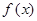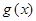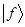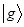Пусть у нас имеется две функции и , рассматривая их как некоторые многомерные функциональные вектора и , определим их скалярное произведение. Очевидно, что при 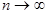, соответствующая сумма:

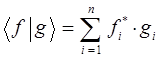
Может разойтись, т.е. при безграничном возрастании 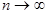, ряд 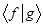перестаёт стремиться к какому-либо пределу. Для того чтобы данный ряд сходился, домножим правую часть данного выражения на величину 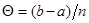- длину участка интервала разбиения 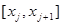, будем иметь соответственно:

Тогда в пределе при 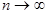полученная сумма перейдёт в интеграл, который и будет представлять собой скалярное произведение функци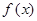й и 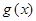, тогда:

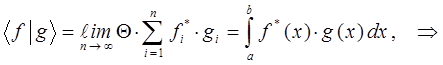
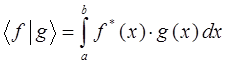
Очевидно при 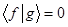- функци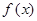и и 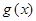будут ортогональны и соответственно при 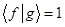- нормированы, т.е.

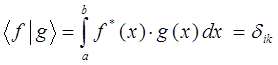
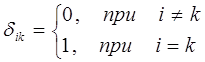
Бесконечномерность пространства функций позволяет записать аналог разложения вектора по-базису в виде некоторого бесконечного ряда:

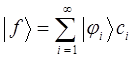
где всей бесконечной совокупности базисных векторов 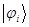отвечает бесконечный набор базисных функций вида: 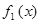, , 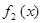, , 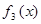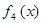…, 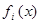. Это в свою очередь означает, что для самой функции можно записать:

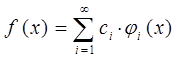
домножая правую и левую части выражения вида:

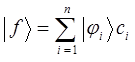
на соответствующий базисный вектор 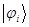, а также с учётом того что набор базисных векторов ортонормирован, т.е. для него справедливы условия вида:

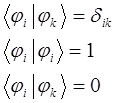
поскольку:

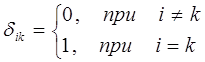
тогда соответственно:

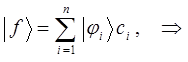
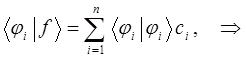
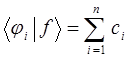
или в окончательном виде:

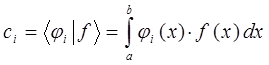
Необходимость преобразования векторов друг в друга приводит к общему понятию оператора, действующего в некотором векторном пространстве 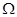. Оператором 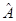называется линейное отображение (операция) вида:

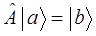
в ходе которого каждому многомерному вектору 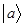из некоторого конечномерного векторного пространства 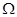, ставится в соответствие новый вектор из того же 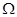- пространства. Это в свою очередь означает, что оператором является некоторое математическое действие (операция), позволяющее исходную функцию одного вида 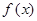- оригинал, «перевести» в функцию другого вида 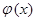- отображение.

Оператор считается заданным, если указано не только правило, с помощью которого он «преобразует» одну функцию (многомерный вектор) в другую, но и, то множество функций, на которые действует данный оператор. Множество функций, на которые может действовать оператор, называется областью определения этого оператора. Среди всех возможных операторов, известны следующие тривиальные операторы:

1. Нулевой оператор 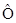переводит все вектора в нуль, т.е. .

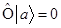2. Единичный оператор 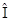(оператор идентичности) – умножает все вектора на единицу, не изменяя, таким образом, вектора .

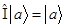3. Скалярный оператор 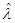- умножает все вектора на скаляр (число), растягивая все вектора в 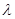раз, т.е. .

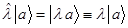4. Обратный оператор 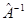- определён так, что из выражения 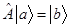можно найти 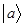, т.е. что .

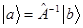Таким образом, если по-определению оператор 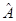переводит функцию (вектор) 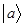в функцию (вектор) , то обратный оператор 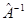осуществляет обратное действие – переводит вектор в 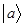; т.е. операторы 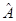и 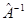есть взаимообратные операции, таковыми являются, например операции: дифференцирования и интегрирования, возведение в степень и извлечение корня, умножение на число и деление на то же самое число, логарифмирование и потенцирование и т.д. Не для каждого оператора существует обратный ему оператор. Так, оператор умножения на нуль 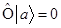- не имеет обратного оператора, поскольку из равенства вида: 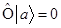, при 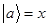следует что: 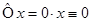, т.е. нельзя найти переменную 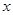. Достаточно очевидно, что обратный оператор 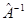удовлетворяет тождеству: 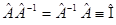. В квантовой механике используют операторы только лишь определённого класса: так называемые линейные самосопряжённые (эрмитовые) операторы. Оператор называется линейным, если выполняется условие вида:

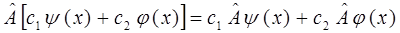
Рассматривая функци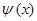и и 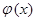как некоторые многомерные векторы некоторого конечномерного векторного пространства 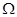, запишем свойство линейности оператора в терминах скобок Дирака:

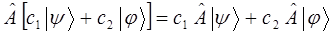
К линейным относят операторы интегрирования и дифференцирования, а также скалярный оператор. Нелинейными являются операторы возведения в степень и извлечение корня. Самосопряжённым (эрмитовым) называется оператор, если для двух интегрируемых функци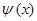й и 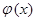или соответствующих им многомерных векторов 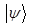и 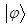, выполняется соотношение вида:

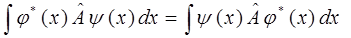
Действительно, так как:

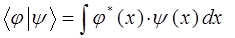
то очевидно выражение не изменится, если подействовать на вектор 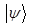единичным оператором (идентичности) 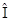, тогда соответственно будем иметь:

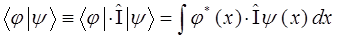
т.к.

очевидно, аналогичное выражение для комплексного сопряжения векторов 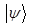и 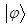будем иметь и в случае действия на одного из них единичного оператора :

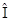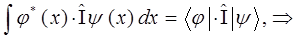
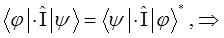
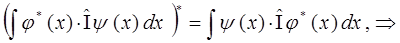
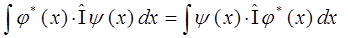
Достаточно очевидно, что выражение, полученное для единичного оператора (идентичности) может быть распространено на любой класс операторов обладающих свойством эрмитовости, поэтому:

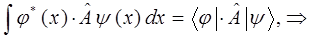
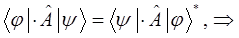
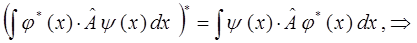
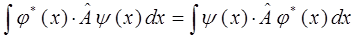
таким образом, находим, что:

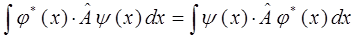
Примерами эрмитовых операторов, играющих важную роль в квантовой механике являются:

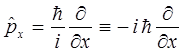
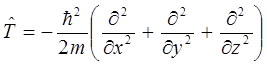
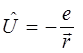
Сумма (разность) линейных операторов есть новый оператор 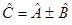, действующий на произвольный вектор 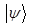, т.е.

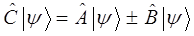
Сумма линейных эрмитовых операторов обладает свойствами коммутативности

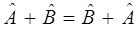
и ассоциативности:

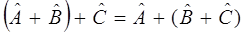
Произведением двух и большего числа операторов называется оператор вида:

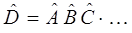
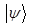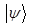
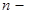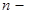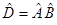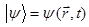действующий на произвольный вектор . Действие данного оператора сводится к последовательному выполнению над вектором операций, где число перемножаемых между собой операторов, т.е. если и , тогда:

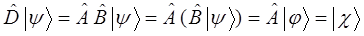
Очевидно, произведение двух и большего числа одинаковых операторов будет определяться выражением вида:

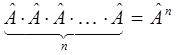
Произведение линейных самосопряжённых операторов обладает свойствами: ассоциативности, дистрибутивности и коммутативности:

1. Свойство ассоциативности:

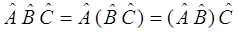
2. Свойство дистрибутивности:

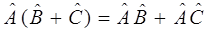
3. Свойство коммутативности: В общем случае действие оператора 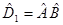не совпадает с действием оператора 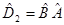, т.е. 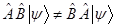, поэтому свойство коммутативности для произведения операторов 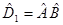и 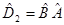не выполняется. Если же два оператора имеют одну и ту же область определения и одинаковым образом действуют на вектор 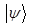, то это будет выражаться равенством вида:

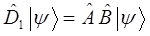
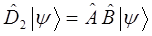
и

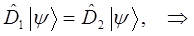
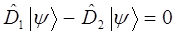
В противном случае операторы не равны между собой, имеют различные области определения и соответственно различным образом будут действовать на одну и ту же функцию (вектор) и свойством коммутативности таким образом обладать не будут. Если же имеет место равенства вида:

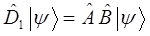
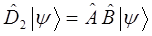
тогда соответственно:

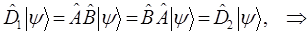
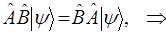
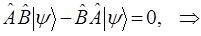
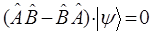
и соответствующие операторы будут коммутировать между собой. В противном случае, т.е. когда выполняется условие вида:

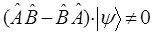
операторы 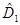и 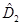коммутировать между собой не будут. Выражение, заключённое в скобках:

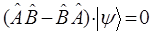
называется коммутатором двух операторов 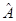и 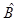. Используя понятие коммутатора 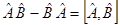, представим последнее выражение в виде:

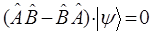
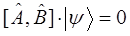
тогда условие коммутативности, выраженное через коммутатор двух операторов 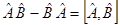, можно записать в виде:

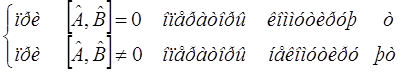
Сформулируем теперь свойства коммутаторов:

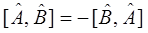
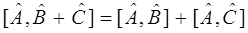
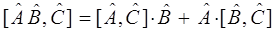
Основываясь на свойствах коммутаторов, решают задачу об одновременной измеримости двух динамических переменных (физических величин) в квантовой механике. Действительно, пусть у нас имеется две взаимосвязанные динамические переменные (физические величины), которым отвечают соответствующие им квантово-механические операторы 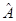и 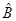. При этом каждому из операторов соответствует свой набор собственных значений физической величины, которой в квантовой механике ставится в соответствие линейный самосопряжённый оператор. В квантовой механике взаимосвязь между операторами и динамическими переменными (физическими величинами) – оригиналами и их отображениями, выражается соответствующими операторными уравнениями вида:

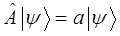
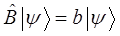
тогда соответственно:

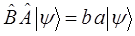
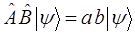
Для решения принципиального вопроса касающегося одновременной измеримости двух взаимосвязанных физических величин (динамических переменных), составим соответствующее этим операторам коммутационное соотношение. При этом если данные операторы будут коммутировать между собой, т.е. если 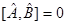, то имеется отличная от нуля возможность одновременного измерения соответствующих этим операторам динамических переменных. Отличие же коммутаторов от нуля, т.е. если 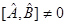, указывает на то, что совместное измерение двух динамических переменных (физических величин) в квантовой механике невозможно (операторы не коммутируют между собой), имеем соответственно:

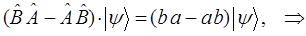
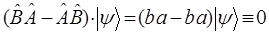
таким образом:

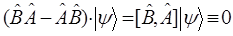
Это в свою очередь находится в полном соответствии с принципом неопределённости В. Гейзенберга, отрицающий возможность одновременного измерения двух динамических переменных (физических величин).

Тогда система уравнений вида:

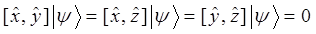
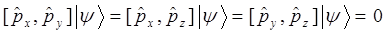
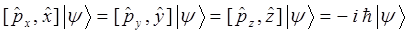
будет представлять собой математическое выражение принципа неопределённости В. Гейзенберга, сформулированного на языке операторов квантовой механики.

Задачей на собственные значения оператора, называют операторное уравнение вида:

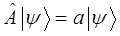
здесь 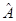- линейный самосопряжённый (эрмитовый) оператор; 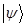- собственные функции оператора; 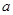- собственные значения оператора, которые представляют собой допустимые значения динамической переменной (физической величины), которой ставится в соответствие линейный самосопряжённый (эрмитовый) оператор. Поэтому указанное выше операторное уравнение может быть переписано соответственно в виде:

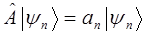
Решить задачу на собственные значения оператора, означает найти такой набор функций 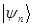, которые «растягиваются» в 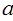- раз (умножаются в 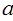- раз) под действием данного оператора 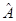. Неизвестными в данной задаче являются как собственные функции 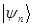, так и собственные значения (числа) 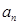. Если решение задачи на собственные значения оператора даёт 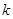- значений и эти собственные значения оператора оказываются одинаковыми, то говорят о вырождении, т.е.

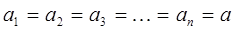
При этом собственные значения, а также соответствующие им собственные функции называют 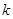- кратно вырожденными.

Приведём ряд важных теорем (опуская их доказательства, выходящие за рамки данной работы), в которых отражены свойства задачи на собственные значения.

Th.1: «Если оператор 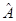эрмитов, то все его собственные значения являются действительными числами».

Th.2: «Если оператор 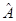эрмитов, а собственные значения этого оператора 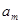и 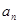различны, то соответствующие собственные функции (векторы) 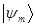и 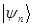взаимно ортогональны», т.е. имеем:

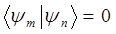
Th.3: «Система собственных функций (векторов) 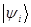эрмитова оператора полна, т.е. любую функцию 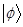, принадлежащую тому же пространству, что и набор собственных функций оператора можно представить в виде суммы:

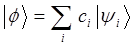
поскольку:

=

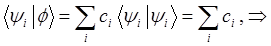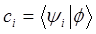
здесь 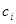- некоторые действительные (вещественные) числа, определяемые как коэффициенты Фурье».

Th.4: «Если несколько собственных функций (векторов) принадлежит одинаковым собственным значениям (случай вырождения), то любая их линейная комбинация является решением той же задачи на собственное значение с тем же собственным значением».

Th.5: «Если система собственных функций (векторов) оператора 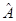является в то же время и системой собственных функций оператора 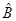, то оператора 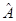и 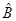коммутируют».

Th.6: «Если операторы 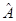и 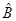коммутируют, то они имеют общую систему собственных функций».