1) Вычислить скалярное произведение векторов  и
и  , если известно:
, если известно:
а) |  |=2, |
|=2, |  |=3, (
|=3, (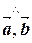 )=
)= 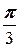 ;
;
б) |  |=3, |
|=3, |  |=1, (
|=1, (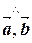 )=
)= 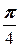 ;
;
в) |  |=4, |
|=4, |  |=2, (
|=2, (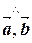 )=
)= 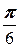 .
.
Решение. а) По определению скалярного произведения имеем
( ,
,  )=|
)=|  |×|
|×|  |×cos(
|×cos(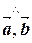 )=2×3×cos
)=2×3×cos 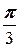 =6×
=6× 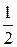 =3.
=3.
Ответ: а) ( ,
,  )=3.
)=3.
2) Найти скалярные произведения, если  и
и  для а), б), в) - соответствующие векторы из упр. 1):
для а), б), в) - соответствующие векторы из упр. 1):
а) (3  +4
+4  , -2
, -2  );
);
б) (2  , 3
, 3  -2
-2  );
);
в) (2  +4
+4  , -3
, -3  -2
-2  );
);
г) ( -4
-4  , 3
, 3  -5
-5  ),
),  и
и  ортогональны и |
ортогональны и |  |=|
|=|  |=1.
|=1.
Решение. а) По 3.1.3 имеем
(3  +4
+4  , -2
, -2  )=3×(-2)×(
)=3×(-2)×( ,
,  )+4×(-2)×(
)+4×(-2)×( ,
,  )
) 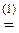 -6
-6 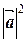 -8×3=(-6)×4-24=-48.
-8×3=(-6)×4-24=-48.
á(1) Воспользовались тем, что (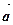 ,
, 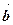 )=(
)=(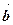 ,
, 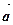 )=3 (см. решение упр.1.а)) и (
)=3 (см. решение упр.1.а)) и (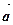 ,
, 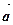 )=
)= 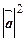 =22=4ñ.
=22=4ñ.
Ответ: а) (3  +4
+4  , -2
, -2  )=-48.
)=-48.
3) Векторы  и
и  ортогональны, вектор
ортогональны, вектор  образует с ними углы, равные
образует с ними углы, равные 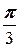 и
и 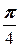 соответственно, |
соответственно, |  |=2, |
|=2, |  |=3, |
|=3, |  |=4. Найти:
|=4. Найти:
а) (3  -4
-4  , 2
, 2  -5
-5  );
);
б) (3  +4
+4  -2
-2  , -3
, -3  +2
+2  );
);
в) (3  -4
-4  +5
+5  )2;
)2;
г) (-3  -2
-2  +6
+6  )2.
)2.
Решение. а) Имеем
(3  -4
-4  , 2
, 2  -5
-5  )=3×2(
)=3×2( ,
,  )-4×2
)-4×2 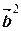 -3×5(
-3×5( ,
,  )+4×5(
)+4×5( ,
,  )=Ä
)=Ä
Так как  и
и  ортогональны, то (
ортогональны, то ( ,
,  )=0. Далее,
)=0. Далее, 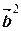 =
= 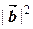 =32=9,
=32=9,
( ,
,  )=|
)=|  |×|
|×|  |×cos(
|×cos(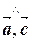 )=2×4×cos
)=2×4×cos 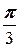 =8×
=8× 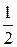 =4,
=4,
( ,
,  )=|
)=|  |×|
|×|  |×cos(
|×cos(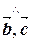 )=3×4×cos
)=3×4×cos 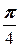 =12×
=12× 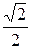 =6
=6 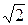 .
.
Поэтому равенство Ä продолжаем:
(-8)×9-15×4+20×6 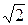 =-132+120
=-132+120 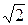 .
.
Таким образом (3  -4
-4  , 2
, 2  -5
-5  )=-132+120
)=-132+120 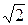 .
.
в) Указание. (3  -4
-4  +5
+5  )2=(3
)2=(3  -4
-4  +5
+5  , 3
, 3  -4
-4  +5
+5  ), и далее, как и выше.
), и далее, как и выше.
Ответ: а) (3  -4
-4  , 2
, 2  -5
-5  )=-132+120
)=-132+120 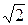 .
.
4) Векторы  и
и  заданы своими координатами. Найти скалярное произведение между этими векторами и угол между ними. В частности, проверить ортогональность векторов:
заданы своими координатами. Найти скалярное произведение между этими векторами и угол между ними. В частности, проверить ортогональность векторов:
а)  =(2; -1),
=(2; -1),  =(3; 2);
=(3; 2);
б)  =(2; -1),
=(2; -1),  =(1; 2);
=(1; 2);
в)  =(3; 1),
=(3; 1),  =(2; 2);
=(2; 2);
г)  =(3; 1),
=(3; 1),  =(1; -3);
=(1; -3);
д)  =(1; -2; 3),
=(1; -2; 3),  =(4; 2; -1);
=(4; 2; -1);
е)  =(1; -2; 3),
=(1; -2; 3),  =(1; 1; 2);
=(1; 1; 2);
ж)  =(1; 1; 2),
=(1; 1; 2),  =(-1; -1; 1).
=(-1; -1; 1).
Решение. б) Аналог формулы (3.2) скалярного произведения в координатах для векторов  =(ax, ay) и
=(ax, ay) и  =(bx, by) на плоскости принимает вид (
=(bx, by) на плоскости принимает вид ( ,
,  )= axbx + ayby. Поэтому (
)= axbx + ayby. Поэтому ( ,
,  )=2×1+(-1)×2=0, то есть (
)=2×1+(-1)×2=0, то есть ( ,
,  )=0 и векторы
)=0 и векторы  и
и  ортогональны.
ортогональны.
д) По формуле (3.2) имеем ( ,
,  )=1×4+(-2)×2+3×(-1)=-3, то есть (
)=1×4+(-2)×2+3×(-1)=-3, то есть ( ,
,  )=-3. По формуле (3.3) получаем
)=-3. По формуле (3.3) получаем
cos(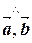 )=
)= 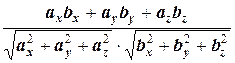 =-
=- 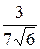 ,
,
так как
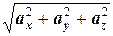 =
= 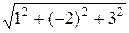 =
= 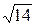 и
и 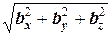 =
= 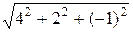 .
.
Тогда (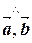 )=arccos
)=arccos 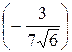 »1,75 (рад) (значения функции arccos можно вычислить на калькуляторе или с использованием компьютера (например, в системе Excel)). В частности, векторы не ортогональны.
»1,75 (рад) (значения функции arccos можно вычислить на калькуляторе или с использованием компьютера (например, в системе Excel)). В частности, векторы не ортогональны.
Ответ: б) ( ,
,  )=0, в частности, векторы
)=0, в частности, векторы  и
и  ортогональны;
ортогональны;
д) (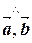 )»1,75 (рад), в частности, векторы не ортогональны.
)»1,75 (рад), в частности, векторы не ортогональны.
5) Известно, что вектор 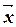 ортогонален векторам
ортогонален векторам  и
и  и удовлетворяет условию (
и удовлетворяет условию (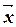 , 2
, 2  +3
+3  -2
-2  )= s. Найти
)= s. Найти 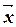 :
:
а)  =(3; 2; 1),
=(3; 2; 1),  =(2; -1; 3), s =2;
=(2; -1; 3), s =2;
б)  =(2; -3; 4),
=(2; -3; 4),  =(1; -2; 4), s =3.
=(1; -2; 4), s =3.
Решение. а) Требуется найти координаты вектора 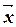 . Положим
. Положим 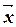 =(a, b, g). Тогда (
=(a, b, g). Тогда ( ,
, 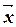 )=3 a +2 b + g и (
)=3 a +2 b + g и ( ,
, 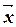 )=2 a - b +3 g. Так как (
)=2 a - b +3 g. Так как ( ,
, 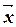 )=(
)=( ,
, 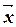 )= =0, то 3 a +2 b + g =0 и 2 a - b +3 g =0. Учитывая, что (
)= =0, то 3 a +2 b + g =0 и 2 a - b +3 g =0. Учитывая, что (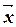 , 2
, 2  +3
+3  -2
-2  )=2, получаем ещё одно уравнение 2 a +3 b - g =2 и приходим к системе с неизвестными a, b, g:
)=2, получаем ещё одно уравнение 2 a +3 b - g =2 и приходим к системе с неизвестными a, b, g:
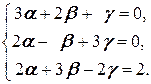
Её решение - (2; -2; -2), то есть 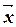 =(2; -2; -2).
=(2; -2; -2).
Ответ: а) 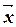 =(2; -2; -2).
=(2; -2; -2).
6) Найти внутренние углы треугольника ABC, если вершины треугольника заданы своими координатами:
а) A (3; 2), B (4; -1), С (2; 8);
б) A (1; 2), B (2; 1), С (2; 8);
в) A (3; 2; -1), B (4; -1; 8), С (2; 4, -1);
г) A (2; 1; 1), B (3; -2; 1), С (1; 2, 3).
Решение. а) Углы треугольника будем искать как углы между векторами, построенными на сторонах треугольника: 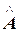 =(
=(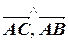 ),
), 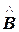 =(
=(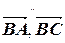 ),
), 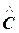 =(
=(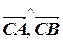 ). Найдём координаты соответствующих векторов:
). Найдём координаты соответствующих векторов:
 =(2-3; 8-2)=(-1; 6),
=(2-3; 8-2)=(-1; 6),  =(4-3; -1-2)=(1; -3),
=(4-3; -1-2)=(1; -3),
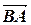 =-
=-  =(-1; 3),
=(-1; 3), 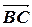 =(-2; 9),
=(-2; 9), 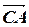 =-
=-  =(1; -6),
=(1; -6), 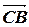 =(2; -9)
=(2; -9)
Далее действуем как в упражнении 4) (завершить решение примера!).
 2015-03-08
2015-03-08 1423
1423
