Определение. Декартова система координат (О, e 1, e 2, e 3) в пространстве называется прямоугольной, если e 1, e 2, e 3 – взаимно перпендикулярные единичные векторы.
Три прямые, проходящие через точку О и параллельные векторам e 1, e 2, e 3,называют осями координат и обозначают соответственно Ох (ось абсцисс), Оу (ось ординат), Оz (ось аппликат). Единичные векторы координатных осей Ох, Оу, Оz, равные базисным векторам e 1, e 2, e 3, обычно обозначают соответственно i, j, k. Декартову прямоугольную систему координат в пространстве будем обозначать Охуz.
Определение. Координатами точки М в декартовой прямоугольной системе координат Охуz называют координаты ее радиуса-вектора 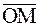 в этой системе.
в этой системе.
Иначе говоря, координаты точки М – это такие три числа x, y, z, что
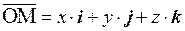 . Координаты х и у называют, соответственно, абсциссой и ординатой точки М, третью координату z называют аппликатой точки М.
. Координаты х и у называют, соответственно, абсциссой и ординатой точки М, третью координату z называют аппликатой точки М.
Определение. Координатами вектора a в пространстве в декартовой прямоугольной системе координат Охуz называют координаты этого вектора в базисе e 1, e 2, e 3.
Операции над векторами, заданными координатами в декартовой прямоугольной системе координат в пространстве, определяются аналогично тому, как это было сделано для плоскости: если даны точки А(х 1, у 1, z 1) и В(х 2, у 2, z 2) в декартовой прямоугольной системе координат Охуz, то 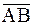 = (
= (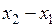 ,
,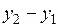 ,
,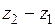 );
);
произведением вектора 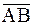 = (
= (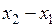 ,
,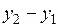 ,
,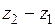 ) на число k будет вектор k
) на число k будет вектор k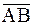 = (k(
= (k(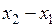 ), k(
), k(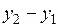 ), k(
), k(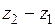 ));
));
скалярное произведение векторов a = (a 1, a 2, a 3) и b = (b 1, b 2, b 3) определим по формуле (1.19): 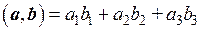 ;
;
длина вектора 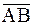 определяется по формуле
определяется по формуле
АВ = 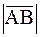 =
=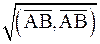 =
=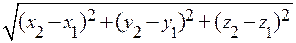 .
.
 2014-02-12
2014-02-12 663
663







