Линия на плоскости есть совокупность точек этой плоскости, обладающих определенными свойствами, при этом точки, не лежащие на данной линии, этими свойствами не обладают. Уравнение линии определяет аналитически выраженное соотношение между координатами точек, лежащих на этой линии. Пусть это соотношение задано уравнением
F(x,y)=0. (2.1)
Пара чисел, удовлетворяющая (2.1), – не произвольная: если х задано, то у не может быть каким угодно, значение у связано с х. При изменении х изменяется у, и точка с координатами (х,у) описывает данную линию. Если координаты точки М0(х 0, у 0) удовлетворяют уравнению (2.1), т.е. F(х 0, у 0)=0 – верное равенство, то точка М0 лежит на данной линии. Верно и обратное утверждение.
Определение. Уравнением линии на плоскости называется уравнение, которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты точек, не лежащих на этой линии.
Если известно уравнение некоторой линии, то исследование геометрических свойств этой линии можно свести к исследованию ее уравнения – в этом заключается одна из основных идей аналитической геометрии. Для исследования уравнений существуют хорошо разработанные методы математического анализа, которые упрощают изучение свойств линий.
При рассмотрении линий используется термин текущая точка линии – переменная точка М(х,у), перемещающаяся вдоль этой линии. Координаты х и у текущей точки называются текущими координатами точки линии.
Если из уравнения (2.1) можно явным образом выразить у
через х, т. е. записать уравнение (2.1) в виде 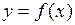 , то кривую, определяемую таким уравнением, называют графиком функции f(х).
, то кривую, определяемую таким уравнением, называют графиком функции f(х).
Примеры.
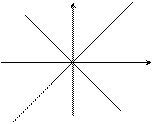
1. Дано уравнение: 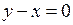 , или
, или 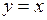 . Если х принимает произвольные значения, то у принимает значения, равные х. Следовательно, линия, определяемая этим уравнением, состоит из точек, равноотстоящих от координатных осей Ох и Оу – это биссектриса I–III координатных углов (прямая
. Если х принимает произвольные значения, то у принимает значения, равные х. Следовательно, линия, определяемая этим уравнением, состоит из точек, равноотстоящих от координатных осей Ох и Оу – это биссектриса I–III координатных углов (прямая  на рис. 2.1).
на рис. 2.1).
Уравнение 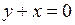 , или
, или 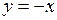 , определяет биссектрису II–IV координатных углов (прямая
, определяет биссектрису II–IV координатных углов (прямая  на рис. 2.1).
на рис. 2.1).
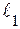 у
у  у
у  у
у
С 
0 х 0 х С 0 х
рис. 2.1 рис. 2.2 рис. 2.3
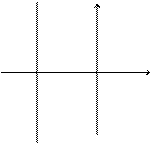
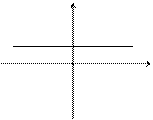
2. Дано уравнение: 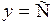 , где С – некоторая постоянная. Это уравнение можно записать иначе:
, где С – некоторая постоянная. Это уравнение можно записать иначе:  . Этому уравнению удовлетворяют те и только те точки, ординаты у которых равны С при любом значении абсциссы х. Эти точки лежат на прямой, параллельной оси Ох (рис. 2.2). Аналогично, уравнение
. Этому уравнению удовлетворяют те и только те точки, ординаты у которых равны С при любом значении абсциссы х. Эти точки лежат на прямой, параллельной оси Ох (рис. 2.2). Аналогично, уравнение 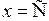 определяет прямую, параллельную оси Оу (рис. 2.3).
определяет прямую, параллельную оси Оу (рис. 2.3).
Не всякое уравнение вида F(x,y)=0 определяет линию на плоскости: уравнению 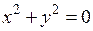 удовлетворяет единственная точка – О(0,0), а уравнению
удовлетворяет единственная точка – О(0,0), а уравнению 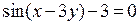 не удовлетворяет ни одна точка на плоскости.
не удовлетворяет ни одна точка на плоскости.
В приведенных примерах мы по заданному уравнению строили определяемую этим уравнением линию. Рассмотрим обратную задачу: составить по заданной линии ее уравнение.
3. Составить уравнение окружности с центром в точке Р(a,b) и
радиусом R.
○ Окружность с центром в точке Р и радиусом R есть совокупность точек, отстоящих от точки Р на расстоянии R. Это значит, что для любой точки М, лежащей на окружности, МР= R, если же точка М не лежит на окружности, то МР ≠ R.
Возьмем на окружности произвольную (текущую) точку М(х,у).
Тогда расстояние от М до Р, или длина вектора
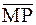 = –
= –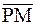 =(
=(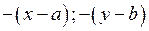 ), равно R, т.е.
), равно R, т.е.
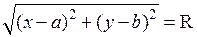 . (2.2)
. (2.2)
Это и есть уравнение окружности, так как:
1) если точка М(х,у) принадлежит окружности, то ее координаты х и у удовлетворяют уравнению (2.2), поскольку 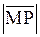 = R.
= R.
2) если точка N(x,y) не лежит на окружности, то ее координаты не удовлетворяют уравнению (2.2), поскольку в этом случае расстояние от N до Р не равно R.
Уравнение (2.2) можно упростить, возведя в квадрат правую и левую части: 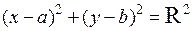 .
.
Если центр Р окружности совпадает с началом координат, то 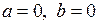 и уравнение принимает вид
и уравнение принимает вид 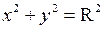 . ●
. ●
 2014-02-12
2014-02-12 4578
4578
