Квадратичные формы

Квадратичной формой L от n переменных 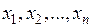называется сумма, каждый член которой является или квадратом одной из этих переменных, или произведением двух разных переменных.

Считая, что в квадратичной форме L уже сделано приведение подобных членов, введем следующие обозначения для коэффициентов этой формы: коэффициент при 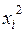обозначим через 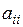, а коэффициент при произведении 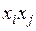для 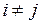– через 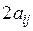. Так как 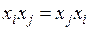, то коэффициент при этом произведении мог бы быть обозначен и через 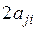, т.е. введенные нами обозначения предполагают справедливость равенства 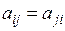. Член 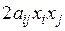можно записать теперь в виде

,

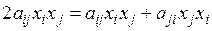а всю квадратичную форму L – в виде суммы всевозможных членов 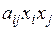, где i и j уже независимо друг от друга принимают значения
от 1 до n:

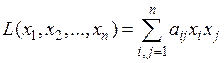(6.13)

Из коэффициентов 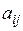можно составить квадратную матрицу 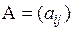порядка n; она называется матрицей квадратичной формы L, а ее ранг – рангом этой квадратичной формы. Если, в частности, 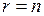, т.е. матрица – невырожденная, то и квадратичная форма L называется невырожденной. Так как 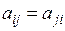, то элементы матрицы А, симметричные относительно главной диагонали, равны между собой, т.е. матрица А – симметричная. Обратно, для любой симметричной матрицы А n -го порядка можно указать вполне определенную квадратичную форму (6.13) от n переменных, имеющую элементы матрицы А своими коэффициентами.

Квадратичную форму (6.13) можно представить в матричном виде, используя введенное в п. 3.2 умножение матриц. Обозначим через Х столбец, составленный из переменных

.

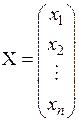Х является матрицей, имеющей n строк и один столбец. Транспонируя эту матрицу, получим матрицу 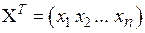, составленную из одной строки. Квадратичная форма (6.13) с матрицей 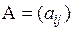может быть записана теперь в виде следующего произведения:

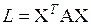(6.14)

В самом деле:

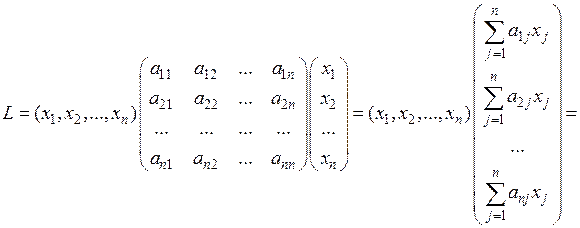
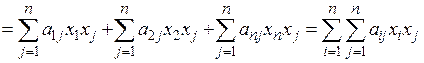
и эквивалентность формул (6.13) и (6.14) установлена.

Пример. Дана квадратичная форма

.

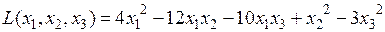Записать ее в матричном виде.

○ Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 4, 1, –3, а другие элементы – половинам соответствующих коэффициентов квадратичной формы. Поэтому

. ●

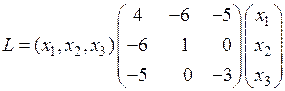Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.

Заметим, что если матрицы А и В таковы, что их произведение определено, то имеет место равенство:

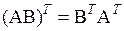(6.15)

Действительно, если произведение АВ определено, то будет определено и произведение 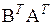: число столбцов матрицы 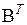равно числу строк матрицы 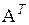. Элемент матрицы 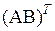, стоящий в ее i -й строке и j -м столбце, в матрице АВ расположен в j -й строке и i -м столбце. Он равен поэтому сумме произведений соответственных элементов j -ой строки матрицы А и i -го столбца матрицы В, т.е. равен сумме произведений соответственных элементов строке j -го столбца матрицы 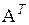и i -й строки матрицы 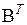. Этим равенство (6.15) доказано.

Пусть матрицы-столбцы переменных 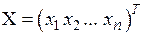и 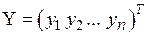связаны линейным соотношением Х = СY, где С = (c_ij) 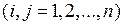есть некоторая невырожденная матрица n -го порядка. Тогда квадратичная форма

,

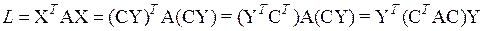или 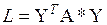, где .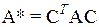

Матрица 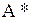будет симметричной, так как в виду равенства (6.15), справедливого, очевидно, для любого числа сомножителей, и равенства 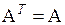, равносильного симметричности матрицы А, имеем:

.

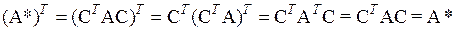Итак, при невырожденном линейном преобразовании Х=СY матрица квадратичной формы принимает вид

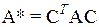. (6.16)

Замечание. Ранг квадратичной формы не меняется при выполнении невырожденного линейного преобразования.

Пример. Дана квадратичная форма

.

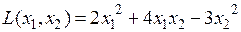Найти квадратичную форму 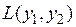, полученную из данной линейным преобразованием

, .

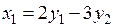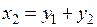○ Матрица данной квадратичной формы 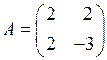, а матрица линейного преобразования 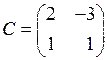. Следовательно, по (6.16) матрица искомой квадратичной формы

,

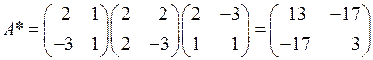а квадратичная форма имеет вид . ●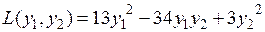

При некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.

Квадратичная форма 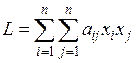называется канонической (или имеет канонический вид), если все ее коэффициенты 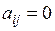при i ≠ j:

,

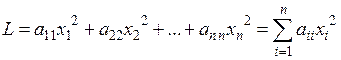а ее матрица является диагональной.

Справедлива следующая теорема.

Теорема 6.1. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.

Пример. Привести к каноническому виду квадратичную форму

.

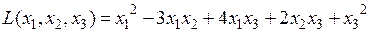○ Вначале выделим полный квадрат при переменной 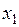, коэффициент при квадрате которой отличен от нуля:

.

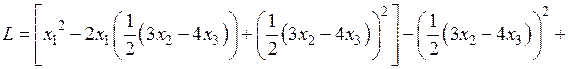
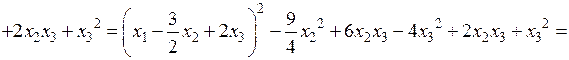
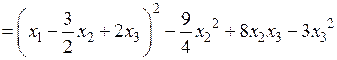Теперь выделим квадрат при переменной 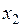, коэффициент при квадрате которой отличен от нуля:

.

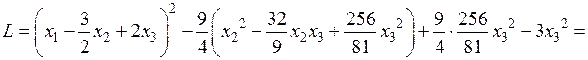
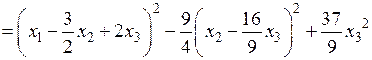Итак, невырожденное линейное преобразование

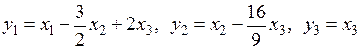
приводит данную квадратичную форму к каноническому виду

.●

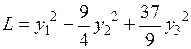Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.

Теорема 6.2. (закон инерции квадратичных форм).

Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.

Например, квадратичную форму

,

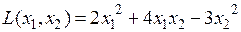которую в рассмотренном на стр. 131 примере мы привели к виду

,

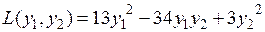можно было, применив невырожденное линейное преобразование

,

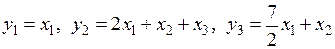привести к виду

.

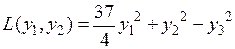Как видим, число положительных и отрицательных коэффициентов (соответственно, два и один) сохранилось.

Заметим, что ранг квадратичной формы равен числу отличных от нуля коэффициентов канонической формы.

Квадратичная форма 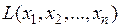называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,

().

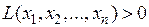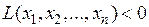Так, например, квадратичная форма 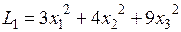является положительно определенной, а форма 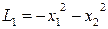– отрицательно определенной.

Положительно определенные и отрицательно определенные квадратичные формы объединены под названием знакоопределенных форм. Если квадратичная форма имеет как положительные, так и отрицательные значения, то она называется знакопеременной.

Теорема 6.3. Для того чтобы квадратичная форма 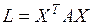была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 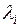матрицы А были положительны (отрицательны).

В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.

Будем рассматривать матрицу квадратичной формы

.

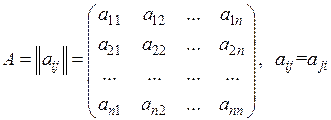Определители

, , , …,

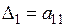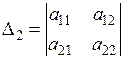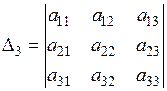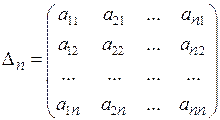
называются главными минорами матрицы А квадратичной формы.

Теорема 6.4. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. .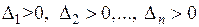

Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки главных миноров 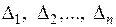чередовались, причем 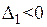, т.е. , .

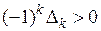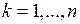Пример. Доказать, что квадратичная форма 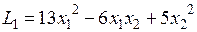является положительно определенной.

○ Первый способ. Матрица А квадратичной формы имеет вид

.

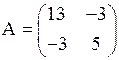Характеристическое уравнение матрицы А

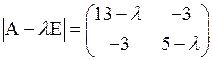
или .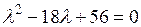

Решая уравнение, найдем 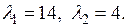Так как корни характеристического уравнение матрицы А положительны, то на основании теоремы 6.3 квадратичная форма L положительно определенная.

Второй способ. Так как главные миноры матрицы А

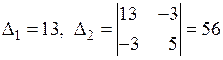
положительны, то по критерию Сильвестра (теорема 6.4) данная квадратичная форма положительно определенная. ●