Линейные преобразования
Функциональная зависимость – одно из основных понятий математики. Мы говорим, что скалярная величина у является функцией скалярного аргумента х, если каждому значению переменной х (взятому из некоторой совокупности значений) соответствует определенное значение переменной у. Закон соответствия обычно записывают в виде 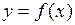 , где f – символическое обозначение функции.
, где f – символическое обозначение функции.
Понятие функциональной зависимости легко обобщается на векторные функции от скалярного аргумента. Мы говорим, что вектор у является вектор-функцией скалярной величины х, если каждому значению скалярной переменной х (взятому из некоторой совокупности значений) соответствует определенное значение переменного вектора у. Закон соответствия обычно записывают в виде 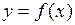 , где f – символическое обозначение функции.
, где f – символическое обозначение функции.
Распространим понятие функциональной зависимости на тот случай, когда не только функция, но и аргумент является вектором.
Если каждому вектору х n-мерного пространства (взятому из некоторой совокупности векторов) соответствует вектор у того же пространства, то такая векторная функция от векторного аргумента называется преобразованием (оператором).
Закон соответствия обычно записывают в виде 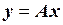 , где А – символическое обозначение преобразования. Вектор
, где А – символическое обозначение преобразования. Вектор 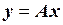 называют образом вектора х.
называют образом вектора х.
Самым простым (и в то же время очень важным) видом преобразования являются линейные преобразования.
Определение. Преобразование А называется линейным, если оно определено для всех векторов пространства, причем для любых векторов х 1 и х 2 и любого скаляра a справедливы равенства
1. 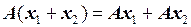 ,
,
2. 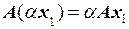 .
.
Из этого определения следует, что линейное преобразование линейного пространства переводит любую линейную комбинацию данных векторов х 1, х 2, …, х k в линейную комбинацию (с теми же коэффициентами) образов этих векторов,
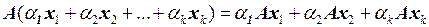 .
.
Среди линейных преобразований особую роль играют следующие простые преобразования:
тождественное преобразование Е, ставящее в соответствие каждому вектору этот же самый вектор, т.е.
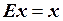 ,
,
нулевое преобразование О, ставящее в соответствие каждому
вектору х нулевой вектор:
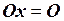 .
.
Примеры. 1. Рассмотрим трехмерное евклидово пространство R3 и в нем преобразование, состоящее в повороте R3 вокруг какой-либо оси, проходящей через нуль. Каждому вектору х ставится в соответствие вектор 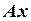 , полученный из него данным поворотом. Условия 1 и 2 легко проверяются. Проверим, например, первое условие:
, полученный из него данным поворотом. Условия 1 и 2 легко проверяются. Проверим, например, первое условие: 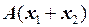 означает, что векторы х 1 и х 2 сначала складываются, а затем полученный вектор поворачивается.
означает, что векторы х 1 и х 2 сначала складываются, а затем полученный вектор поворачивается. 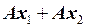 означает, что векторы х 1 и х 2 сперва поворачиваются, а затем складываются. Ясно, что в обоих случаях результат один и тот же.
означает, что векторы х 1 и х 2 сперва поворачиваются, а затем складываются. Ясно, что в обоих случаях результат один и тот же.
2. Пусть R¢ – некоторая плоскость в трехмерном пространстве R3, проходящая через нуль. Поставим в соответствие каждому вектору х его проекцию 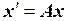 на эту плоскость. Условия 1 и 2 опять легко проверяются. Например, первое условие означает, что проекция суммы равна сумме проекций.
на эту плоскость. Условия 1 и 2 опять легко проверяются. Например, первое условие означает, что проекция суммы равна сумме проекций.
3. Показать, что преобразование 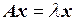 , где
, где 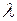 – действительное число, является линейным.
– действительное число, является линейным.
○ Пусть 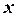 и
и 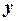 – произвольные векторы n-мерного пространства,
– произвольные векторы n-мерного пространства,
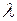 – произвольное действительное число. Найдем образы векторов:
– произвольное действительное число. Найдем образы векторов:
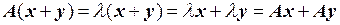 ,
, 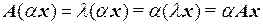 .
.
Оба условия, определяющие линейное преобразование, выполнены, значит, данное преобразование является линейным. Рассмотренное преобразование А называется преобразованием подобия. ●
4. Преобразование А в линейном пространстве R определено равенством 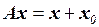 , где
, где 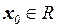 – фиксированный ненулевой вектор. Является ли преобразование А линейным?
– фиксированный ненулевой вектор. Является ли преобразование А линейным?
○ Найдем образы произвольных векторов 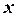 и
и 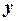 пространства R и их суммы:
пространства R и их суммы: 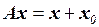 ,
, 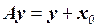 ,
, 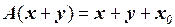 .
.
Так как 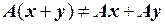 , то преобразование А не является линейным. ●
, то преобразование А не является линейным. ●
5. Выяснить, является ли преобразование 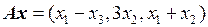 линейным, если вектор
линейным, если вектор 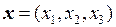 .
.
○ По условию вектор 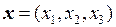 . Пусть вектор
. Пусть вектор 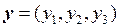 . Тогда по определению операций над векторами:
. Тогда по определению операций над векторами:
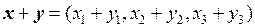 ,
, 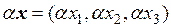 .
.
Найдем образы векторов:
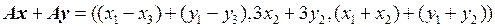 ,
,
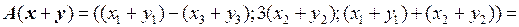
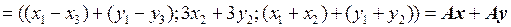 ,
,
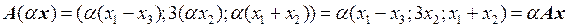 .
.
Так как выполнены оба условия, определяющие линейное преобразование, то преобразование А является линейным. ●
 2014-02-12
2014-02-12 6704
6704
