2014-02-12
484
Лекция 10
ЛИНЕЙНЫЕ ГЕОМЕТРИЧЕСКИЕ ОБЪЕКТЫ (II)
1.Прямая линия в пространстве.
2.Прямая линия на плоскости.
3.Взаимное расположение прямых и плоскостей
Прямая в пространстве определяется как линия пересечения двух пересекающихся плоскостей
где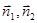 
нормальные векторы плоскосте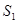й 
и ,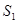 
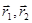- радиус-векторы любых фиксированных точек, принадлежащих этим плоскостям.
Переходя к координатной форме записи, находим
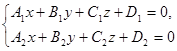- уравнения прямой
в координатной форме,
где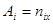
, 
, 
, 
.
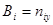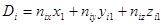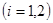Возможны другие формы записи уравнения прямой. Пусть в прямоугольной декартовой системе координат задана прямая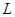 
. Введем в рассмотрение вектор 
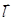, параллельный этой прямой, - направляющий вектор, вектор 
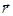- радиус-вектор произвольной точки данной прямой 
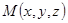и вектор 
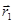- радиус-вектор фиксированной точки прямой 
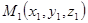. Тогда из условия коллинеарности векторов 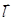и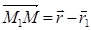 
следует, что 
(
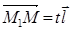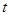- параметр). Т.е
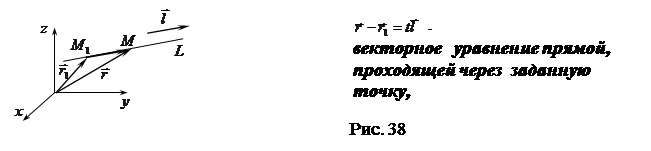
В координатной форме параметрические уравнения имеют вид
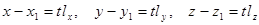
или
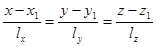- уравнения прямой в
