.
Возможны другие формы записи уравнения плоскости, связанные с различным представлением вектора нормали 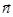 .
.
Если вектор задан своим модулем и направляющими косинусами,
 |
то подстановка этих соотношений в равенство (*) дает

или
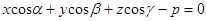 - нормальное уравнение плоскости,
- нормальное уравнение плоскости,
где 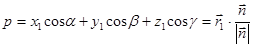 .
.
Параметр 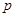 определяет проекцию вектора
определяет проекцию вектора  , проведённого из начала координат в любую точку плоскости на направление вектора нормали в этой точке,
, проведённого из начала координат в любую точку плоскости на направление вектора нормали в этой точке, 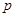 - расстояние от начала координат до плоскости.
- расстояние от начала координат до плоскости.
Пусть 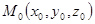 точка, не лежащая в плоскости
точка, не лежащая в плоскости 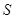 ; а
; а 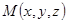 - произвольная точка, лежащая в этой плоскости. Радиус-векторы этих точек -
- произвольная точка, лежащая в этой плоскости. Радиус-векторы этих точек -  и
и  .
.
 |
Отклонение точки от плоскости есть разность проекций радиус- векторов  и
и  на направление нормали. Модуль отклонения равен расстоянию от точки
на направление нормали. Модуль отклонения равен расстоянию от точки 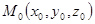 до плоскости
до плоскости 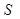 . Отклонение положительно, если точка
. Отклонение положительно, если точка 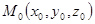 и начало координат лежат по разные стороны от плоскости; в противоположном случае отрицательно. В координатной форме, с учетом
и начало координат лежат по разные стороны от плоскости; в противоположном случае отрицательно. В координатной форме, с учетом 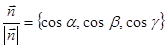 , отклонение от плоскости определяется равенством
, отклонение от плоскости определяется равенством
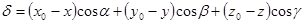 .
.
Для определения расстояния от плоскости до начала координат разделим левую часть уравнения плоскости на модуль вектора нормали
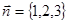 :
: 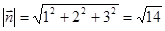 ,
,
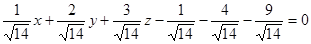 .
.
Искомое расстояние равно 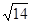 .
.
Подставляя координаты точки 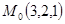 и точки
и точки 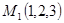 , лежащей в плоскости, в формулу вычисления отклонения, находим
, лежащей в плоскости, в формулу вычисления отклонения, находим
 .
.
Знак минус означает, точка 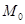 и начало координат лежат по одну сторону от плоскости.
и начало координат лежат по одну сторону от плоскости.
Расстояние между параллельными плоскостями – расстояние от точки, лежащей на одной до другой плоскости.
Пример 3. Записать уравнения плоскостей 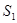 и
и 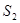 с нормальным вектором
с нормальным вектором 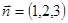 , отстоящих на расстоянии, равном двум от начала координат в направлении вектора
, отстоящих на расстоянии, равном двум от начала координат в направлении вектора 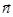 , и в противоположном направлении.
, и в противоположном направлении.
Определим, предварительно, направляющие косинусы вектора 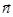

С учетом смысла параметра 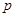 в нормальном уравнении плоскости искомые уравнения имеют вид
в нормальном уравнении плоскости искомые уравнения имеют вид

Пусть 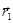 ,
, ,
,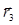 - радиус-векторы фиксированных точек:
- радиус-векторы фиксированных точек: 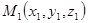 ,
, 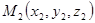 и
и 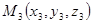 , лежащих в плоскости
, лежащих в плоскости 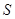 , а
, а  - радиус-вектор произвольной ее точки
- радиус-вектор произвольной ее точки 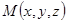 . Тогда, из условия компланарности векторов
. Тогда, из условия компланарности векторов 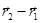 ,
, 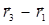 ,
,  , находим
, находим

или по правилу вычисления смешанного произведения векторов


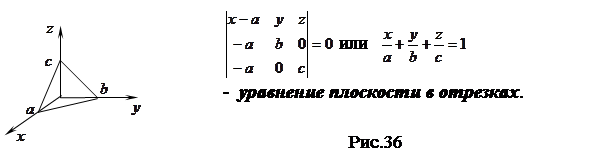 Если в качестве точек
Если в качестве точек 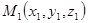 ,
,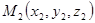 и
и 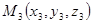 выбрать точки пересечения плоскости
выбрать точки пересечения плоскости 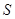 с осями координат(т.е. положить -
с осями координат(т.е. положить - 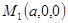 ,
,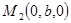 и
и 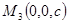 ), то
), то
Пример 4. Составить уравнение плоскости, проходящей через точки 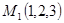 ,
, 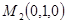 и
и 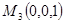 .
.
Воспользовавшись уравнением плоскости, проходящей через три точки, находим

или
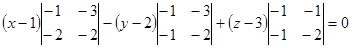 .
.
Окончательно: 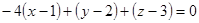 .
.
Пример 5. Составить уравнение плоскости, проходящей через точки 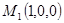 ,
, 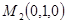 и
и 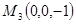 .
.
Поскольку точки 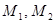 и
и 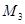 лежат на координатных осях при составлении уравнения плоскости удобно воспользоваться уравнением плоскости в отрезках. При этом
лежат на координатных осях при составлении уравнения плоскости удобно воспользоваться уравнением плоскости в отрезках. При этом 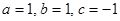 и уравнение имеет вид
и уравнение имеет вид
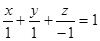 или
или 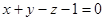 .
.
 2014-02-12
2014-02-12 3942
3942
