Плоскость. Пусть в прямоугольной декартовой системе координат задана плоскость

Пусть в прямоугольной декартовой системе координат задана плоскость 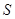. Введем в рассмотрение вектор 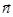, перпендикулярный этой

плоскости, - нормальный вектор, вектор 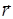- радиус-вектор произвольной точки 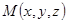данной плоскости и вектор 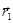- фиксированной точки 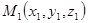плоскости. Тогда из условия перпендикулярности векторов 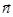и 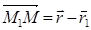их скалярное произведение равно нулю. Т.е.

______________________________

¹⁴Отчетливое и исчерпывающее изложение этого метода и основ аналитической геометрии было сделано Р. Декартом в его «Геометрии» (1637).

Записывая скалярное произведение через координаты перемножаемых векторов, находим уравнение плоскости в координатной форме

. (*)

или

- общее уравнение плоскости,

где

, , , .

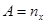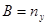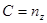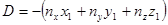Таким образом, любая плоскость может быть задана уравнением первой степени.

Плоскость делит геометрическое пространство на два полупространства 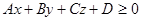и .

Пример 1. Записать уравнение плоскости, проходящей через точку 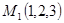, с нормальным вектором .

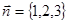В соответствии с уравнением (*) искомое уравнение имеет вид