Записать уравнение прямой 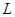 в канонической форме и изобразить ее на чертеже, если прямая задана как линия пересечения двух плоскостей
в канонической форме и изобразить ее на чертеже, если прямая задана как линия пересечения двух плоскостей 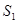 и
и 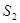 .
.
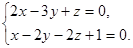
Для того, чтобы записать уравнение прямой в параметрической форме, необходимо знать направляющий вектор прямой и точку, лежащую на прямой.
Направляющий вектор 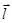 перпендикулярен нормальным векторам
перпендикулярен нормальным векторам 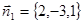 и
и 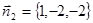 плоскостей
плоскостей  и
и 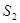 . Из определения векторного произведения.
. Из определения векторного произведения.
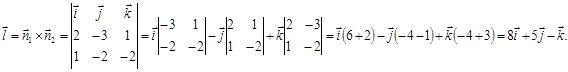
Для определения координат точки, лежащей на прямой, нужно найти частное решение системы уравнений:
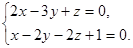
Полагая 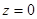 , находим
, находим 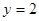 и
и 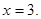
Итак,
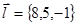 ,
, 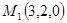 .
.
Уравнение прямой в канонической форме имеет вид:
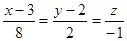 .
.
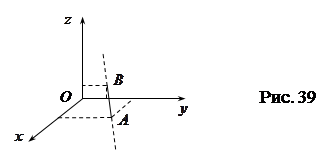 Координаты точки
Координаты точки 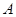 пересечения прямой с плоскостью
пересечения прямой с плоскостью 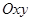 -
-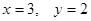 . Координаты точки
. Координаты точки 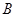 пересечения прямой с плоскостью
пересечения прямой с плоскостью 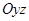 -
-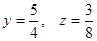 .
.
 2014-02-12
2014-02-12 558
558








