Составление дифференциальных уравнений, структурных схем и
САР скорости вращения гидротурбины (САР СВГТ) состоит из объекта регулирования и двух взаимосвязанных автоматических регуляторов (рис. 2).
· первый – регулирует положение поворотных лопаток направляющего устройства;
· второй – угол поворота лопастей рабочего колеса.
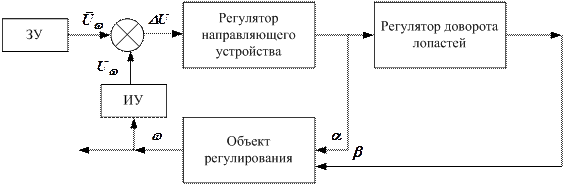
Рисунок 7.2 Упрощенная схема САР СВГТ
Поворот лопасти осуществляется от механического программника, связанного со штоком серводвигателя направляющего аппарата. Оба регулятора изменяют расход воды, протекающий через гидротурбину и ее к.п.д.
С целью упрощения математической выкладки полагаем: угол поворота лопастей рабочего колеса установлен на некоторую постоянную величину и при работе автоматического регулятора, управляющего положением лопаток направляющего аппарата, его величина остается неизменной.
САР СВГТ состоит из следующих основных агрегатов:
· турбина с главным генератором (в виде нагрузки);
· трубопровода;
· главного серводвигателя;
· направляющего аппарата;
· вспомогательного серводвигателя;
· вспомогательного генератора;
· синхронного электродвигателя, вращающего центробежный маятник;
· изодрома.
Составим дифференциальные уравнения, описывающие динамические процессы в агрегатах этой системы
Для простоты вначале пренебрегаем переходными процессами в трубопроводе, представляющего собой, систему с распределенными параметрами, описываемую уравнениями в частных производных.
Тогда: уравнение движения ротора гидротурбины представится в виде:
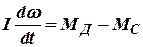 | (1) |
где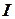 – момент инерции ротора гидротурбины и главного генератора;
– момент инерции ротора гидротурбины и главного генератора;
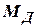 - вращаемый момент, развиваемый гидротурбиной;
- вращаемый момент, развиваемый гидротурбиной;
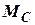 - момент сил сопротивления.
- момент сил сопротивления.
Момент движущих сил зависит от скорости течения воды 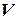 , величины открытия направляющего аппарата
, величины открытия направляющего аппарата 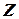 и угловой скорости вращения гидротурбины
и угловой скорости вращения гидротурбины 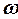
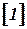 :
:
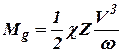 , , | (2) |
где 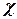 – коэффициент, зависящий от конструкции гидротурбины.
– коэффициент, зависящий от конструкции гидротурбины.
Проведём линеаризацию уравнения (2) с помощью разложения в ряд Тейлора по степеням 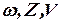 . Для этого примем что
. Для этого примем что
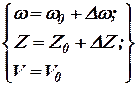 |
где 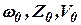 - соответственно, установившееся значение числа оборотов гидротурбины, величины открытия направляющего аппарата и скорости воды. Уравнение (2) при отбрасывании членов разложения второго и более высоких порядков малости примет вид:
- соответственно, установившееся значение числа оборотов гидротурбины, величины открытия направляющего аппарата и скорости воды. Уравнение (2) при отбрасывании членов разложения второго и более высоких порядков малости примет вид:
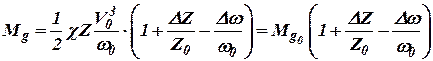 . . | (3) |
Откуда значение установившегося момента гидротурбины
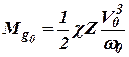 . . | (4) |
Подставив (4) в (3), получим
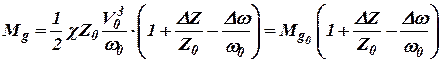 . . | (5) |
Момент сил сопротивления 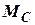 представляют в виде сумы двух величин:
представляют в виде сумы двух величин:
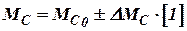 , , | (6) |
где 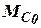 – установившееся значение момента сил сопротивления;
– установившееся значение момента сил сопротивления;
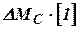 - мгновенное значение нагрузки на гидротурбине (от подключения или отключения потребителей электроэнергии,
- мгновенное значение нагрузки на гидротурбине (от подключения или отключения потребителей электроэнергии,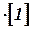 - единичная функция.
- единичная функция.
При подключении нагрузки к генератору выражение (6) берут знак плюс, а при отключении знак минус.
Предположим, что в системе регулирования внезапно отключили часть нагрузки, тогда выражение (1) с учётом (5) и (6) примет вид:
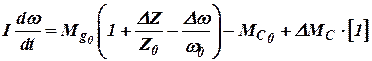 . . | (7.7) |
В установившемся состоянии имеет место равенство момента движущихся сил 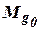 с моментом сил сопротивления
с моментом сил сопротивления 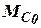 , то есть
, то есть
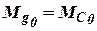 . . | (8) |
Тогда формулу (7) можно переписать так
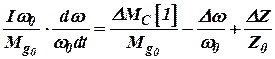 . . | (9) |
Что приводит к форме без размерных параметров. Введём обозначения:
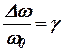 ;
; 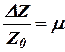 ;
; 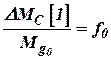 ;
; 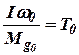 .
.
С учетом введенных обозначений уравнение движения гидротурбины в безразмерной форме запишется как
 , , 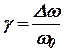 . . | (10) |
Применяя к этому уравнению преобразование Лапласа для случая нулевых начальных условий, имеем:
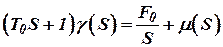 , , 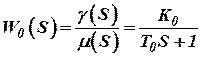 | (11) |
или
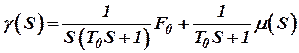 . . | (12) |
 2014-02-09
2014-02-09 1635
1635








