И структурные схемы
Дифференциальные уравнения движения основных звеньев
Лекция №10
Согласно теореме об изменении момента движения для неустановившегося режима:
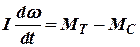 , , | (10.1) |
где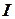 - момент инерции ротора;
- момент инерции ротора;
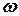 - угловая скорость вращения ротора.
- угловая скорость вращения ротора.
Если роторы турбины и генератора вращаются с различными скоростями 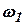 ,
, 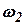 и их моменты инерции
и их моменты инерции 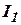 и
и 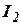 , то в (10.1) необходимо подставлять приведенный момент инерции
, то в (10.1) необходимо подставлять приведенный момент инерции
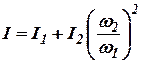 , , |
где 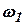 - скорость турбины;
- скорость турбины;
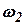 - скорость электрического генератора;
- скорость электрического генератора;
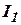 - момент инерции турбины;
- момент инерции турбины;
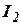 - момент электрического генератора.
- момент электрического генератора.
Для установившегося режима ротор вращается равномерно, что возможно в случае равенства момента движущих сил турбины 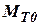 и момента сил сопротивления
и момента сил сопротивления 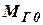
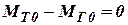 . . | (10.2) |
Вычтем в правых частях почленно уравнение (10.2) из (10.1) и введем обозначения:
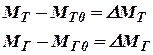 . . |
Тогда уравнение движения ротора примет вид:
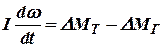 . . | (10.3) |
Момент действующих сил в турбине может быть выражен таким образом:
 , , | (10.4) |
где 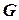 - Расход рабочего тепла турбиной в пч/с;
- Расход рабочего тепла турбиной в пч/с;
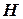 - удельная теоретическая работа в кг м/кг;
- удельная теоретическая работа в кг м/кг;
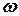 - угловая скорость в рад/с;
- угловая скорость в рад/с;
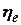 - эффективный КПД турбины.
- эффективный КПД турбины.
Если распределительные органы находятся так близко от турбины, что при их перемещении 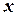 практически мгновенно изменяется расход
практически мгновенно изменяется расход 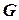 и удельная теоретическая работа
и удельная теоретическая работа 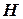 , тот можно считать движущий момент зависит в основном от координат
, тот можно считать движущий момент зависит в основном от координат 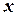 и
и 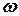 :
:
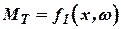 . . | (10.5) |
Момент сил сопротивления генератора для неизменного сопротивления электрической сети можно представить в виде функции:
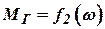 . . | (10.6) |
Уравнения движения ротора составим так, чтобы использовать, что в исследованиях устойчивости регулирования при изучении малых колебаний. Для этого разложим функции 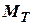 и
и 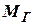 в ряд по степеням
в ряд по степеням 
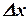 и
и 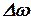 , ограничившись лишь степенями:
, ограничившись лишь степенями:
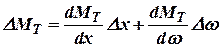 ; ; | 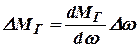 . . |
Подставив эти выражения в (10.3) и обозначив 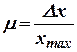 ;
; 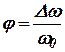 , получим
, получим
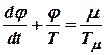 , , | (10.7) |
где
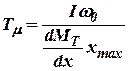 ; ; | (10.8) |
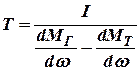 . . | (10.9) |
Динамические постоянные 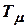 и
и 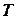 имеют размерность времени и являются постоянными турбогенератора.
имеют размерность времени и являются постоянными турбогенератора.
Выражение (7.7) можно привести к виду 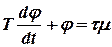 , или в операторной форме
, или в операторной форме
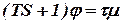 , , |
где 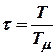 .
.
Данное уравнение содержит одну постоянную времени Т, а безразмерный коэффициент 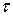 не содержит момента инерции ротора и характеризует статические свойства системы.
не содержит момента инерции ротора и характеризует статические свойства системы.
Динамические константы вычисляют по заданным характеристикам турбины и генератора. Некоторые характеристики могут быть выражены аналитически, но чаще их задают в виде графиков.
В качестве примера на рис.1 показаны графики изменения вращающегося момента турбины от координаты 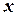 и от
и от 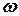 .
.
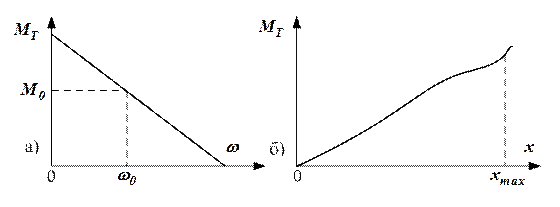
Рисунок 10.1
а) Изменение 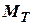 в зависимости от
в зависимости от 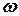 при неизменном расходе рабочего тела (
при неизменном расходе рабочего тела (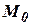 и
и 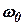 – расчетные величины);
– расчетные величины);
б) Изменение 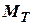 в зависимости от положения клапанов
в зависимости от положения клапанов 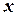 при
при 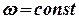 .
.
На рисунке представлен график 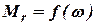 . Графики эти необходимы для вычисления постоянных
. Графики эти необходимы для вычисления постоянных 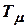 и
и 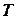 .
.
Так как  , а
, а 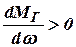 , то
, то 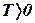 .
.
В некоторых системах составляющая 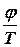 в уравнении (10.7) играет малую роль, тогда можно записать:
в уравнении (10.7) играет малую роль, тогда можно записать:
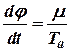 , , | (10.10) |
где
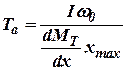 , , | (10.11) |
Если принять для всех режимов работы турбогенератора (ТГ) одно и тоже среднее значение 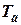 и если предположить, что произошел полный сброс нагрузки и что распределительные органы остаются в открытом положении
и если предположить, что произошел полный сброс нагрузки и что распределительные органы остаются в открытом положении 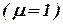 , то время
, то время 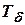 , в течении которого скорость вращения машины достигает ее значения при установившемся движении на холостом ходу, определится из уравнения (10.10):
, в течении которого скорость вращения машины достигает ее значения при установившемся движении на холостом ходу, определится из уравнения (10.10):
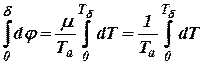 или или 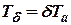 |
Постоянная 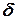 ,
, 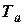 имеет смысл времени разбега ТГ в пределах полного статического изменения скорости вращения
имеет смысл времени разбега ТГ в пределах полного статического изменения скорости вращения 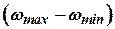 при максимальном и постоянном расходе рабочего тела и неизменных его параметрах.
при максимальном и постоянном расходе рабочего тела и неизменных его параметрах.
 2014-02-09
2014-02-09 3308
3308