Важным эксплуатационным качеством трактора и автомобиля является плавность хода. Недостаточная плавность хода проявляется в возникновении неприятных и вредных колебаний. Колебания вызываются возмущающими силами и зависят от системы подрессоривания, общей компоновки, конструктивных особенностей машины и др. факторов.
Подрессоренная часть автомобиля, как всякое свободное тело в пространстве, обладает шестью степенями свободы и может иметь следующие колебательные движения (рис. 15.1,а):
линейные:
вдоль оси z-z – подпрыгивание,
вдоль оси x-x – подергивание,
вдоль оси y-y – пошатывание;
угловые:
вдоль оси y-y – галопирование,
вдоль оси x-x – покачивание,
вдоль оси z-z – виляние (рыскание).
На рис 15.1,б подрессоренные элементы машины представлены массой m, сосредоточенной в их центре тяжести О. А неподрессоренные – двумя массами m1 и m2, из которых первая представляет собой массу передних колёс, а вторая – массу задних колёс.
Отношение подрессоренных масс к неподрессоренным называют коэффициентом μм подрессоренных масс:
μм = m/(m1+m2),
являющимся важной характеристикой колебательной системы. При снижении веса неподрессоренных масс уменьшается сила толчков, передаваемых подрессоренным массам, а при увеличении веса подрессоренных масс уменьшается их чувствительность к указанным толчкам. Для грузовых автомобилей μм = 4…5.
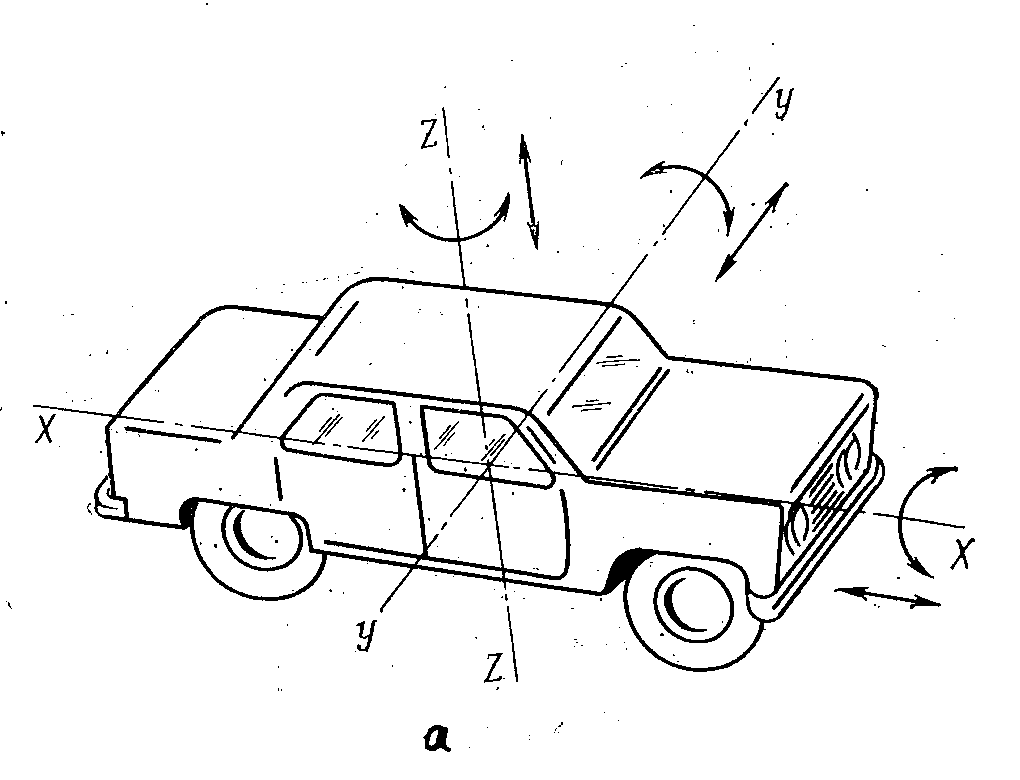
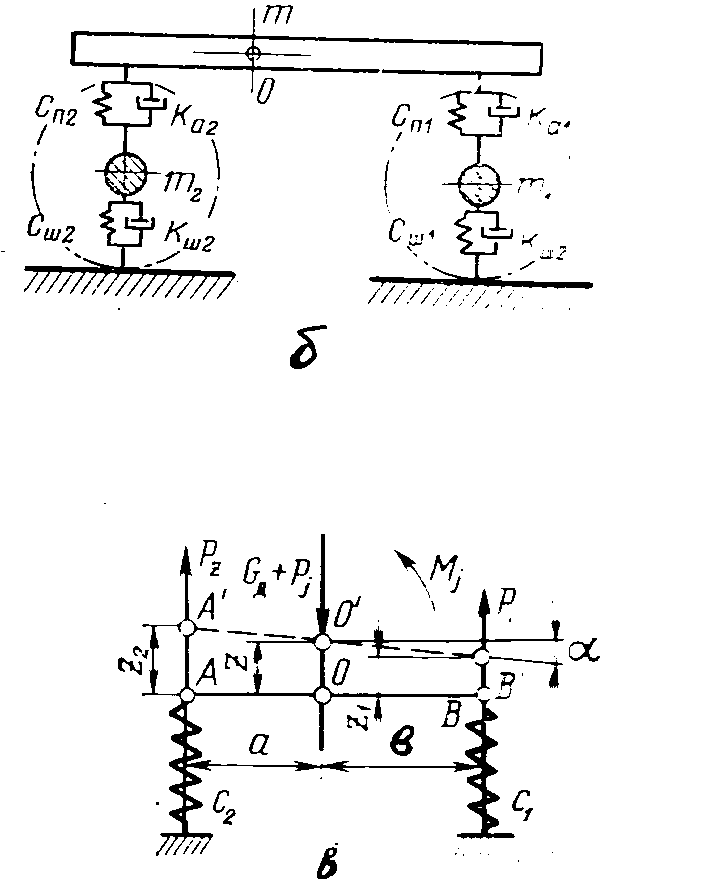
Рисунок 15.1 - Виды колебаний автомобиля (а), схема его колебательной системы (б), эквивалентная колебательная схема кузова (в).
Схема колебательной системы автомобиля, изображённая на рис.15.1,б, состоит из четырёх упругих элементов: передней и задней подвесок с приведенными коэффициентами жёсткости cп1 и cп2, передней и задней шин с коэффициентами жёсткости cш1 и cш2.
Общий коэффициент жёсткости, учитывающий совместные деформации подвески и шин, можно определить из условия, что под действием груза G их суммарный прогиб
f = fп + fш = G/cп + G/cш
где fп – прогиб подвески; fш – прогиб шин.
Отсюда находим общий коэффициент жёсткости
c = G/f = G/(G/cп + G/ cш) = cп cш/(cп + cш). (15.1)
Дифференциальное уравнение свободных вертикальных колебаний центра упругости подрессоренных масс автомобиля (при отсутствии сопротивлений в колебательной системе):
md2z/dt2 + (c1+c2)z = 0, (15.2)
где m – масса подрессоренной части автомобиля; d2z/dt2 – ускорение центра упругости; c1 + c2 – суммарный приведенный коэффициент жёсткости передней и задней подвесок; z – вертикальное перемещение.
Данное уравнение соблюдается при перемещении центра упругости по закону:
z = A·sin 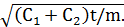
Свободные вертикальные колебания центра упругости совершаются с частотой
ω = 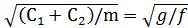
Так как (c1 + c2)/m = ω2, то уравнение (15.2) перепишем в виде:
d2z/dt2 + ω2z = 0 (15.3)
Рассмотрим случай, когда колебательная система автомобиля имеет две степени свободы и может совершать вертикальные и продольные угловые колебания (рис.15.1,б). Условия равновесия этой колебательной системы выражаются двумя уравнениями:
md2z/dt2 + c1z1 + c2z2 = 0
mρ2d2α/dt2 + c2z2a – c1z1в = 0 (15.4)
Проведя в системе уравнений (15.4) преобразования и допущения, введя коэффициенты связи К1= (ав - ρ2)/(а2 + ρ2) и К2= (ав - ρ2)/(в2+ ρ2), получим систему уравнений:
d2z1/dt2 + К1d2z2/dt2 + ω12·z1 = 0
d2z2/dt2 + К2d2z1/dt2 + ω22·z2 = 0 (15.5)
Решая эти уравнения, после некоторых преобразований получаем значения собственных частот Ω1 и Ω2 колебаний точек А и В. Частоты Ω1 и Ω2, называемые также частотами связи в общем случае отличаются от парциальных частот ω1 и ω2. Однако между ними существуют следущие зависимости:
Ω12 = [ 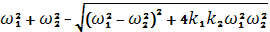 ];
];
Ω22 = [ 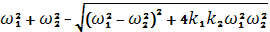 ].
].
На колебания автомобиля существенно влияет распределение его подрессоренных масс, характеризуемое коэффициентом распределения масс,
ε = ρ2/(ав).
Если ε = 1, т.е. когда ρ2 = ав, то коэффициенты связи к1= 0 и к2=0, а собственные частоты равны парциальным: Ω 1= ω1; Ω 2 = ω2.
При ε = 1
ω1= 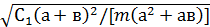 =
= 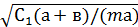 =
= 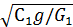 =
= 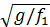 ; ω2=
; ω2= 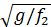
Таким образом, если коэффициент распределения масс ε=1, то колебания передней и задней осей автомобиля не зависимы друг от друга, а частоты этих колебаний равны соответствующим частотам свободных колебаний. Как показали исследования, это благоприятно отражается на колебаниях автомобиля.
Для современных легковых автомобилей ε = 0,9…1,0. Повышение коэффициента ε до указанных пределов достигнуто главным образом увеличением радиуса инерции подрессоренных масс.
Коэффициент распределения масс грузовых автомобилей может изменяться в широких пределах в зависимости от массы перевозимого груза и расположения его на платформе. Изменение нагрузки наиболее существенно отражается на задней подвеске, в то время как нагрузка на переднюю подвеску изменяется незначительно. Чтобы уменьшить разницу в прогибах обеих подвесок, необходимо регулировать упругую характеристику задней подвески. В большинстве случаев для этой цели в заднюю подвеску грузовых автомобилей вводят дополнительные упругие элементы (подрессорники), которые включаются при больших нагрузках.
Основная литература [6, с. 323…326]
Дополнительная литература [13, с. 316…324].
Контрольные вопросы:
1. В чём проявляется недостаточная плавность хода трактора и автомобиля?
2. Что называют коэффициентом подрессоренных масс?
3. Напишите дифференциальное уравнение свободных вертикальных колебаний центра упругости подрессоренных масс автомобиля.
Планы лабораторных занятий
Лабораторная работа №1. Моменты инерции и маховые моменты элементов машин.
Задание.
1.Замерить геометрические параметры маховика, барабана, блока, муфты на натурных образцах.
2. Определить моменты инерции и маховые моменты данных элементов машин.
Рекомендуемая литература:[6] с. 66…67
Контрольные вопросы
1. Чему равен момент инерции маховика?
2. Как определить момент инерции блока?
3. Назовите зависимость для определения махового момента муфты.
Лабораторная работа №2. Суммарные приведенные жесткости конструктивных элементов машин.
Задание
1. Привести эквивалентные схемы механизма подъема стрелы с приводом от гидроцилиндров.
2. Определить суммарную жесткость последовательно расположенных упругих элементов.
3. Определить суммарную жесткость параллельно расположенных упругих элементов.
4. Написать выражение для суммарной жесткости рабочего оборудования (стрелы с гидроприводом), приведенной к ее вершине.
Рекомендуемая литература: [6] с. 88…91.
Контрольные вопросы:
1. Чему равна суммарная приведенная жесткость трех последовательно расположенных упругих элементов?
2. Как определить суммарную приведенную жесткость трех параллельно расположенных упругих элементов?
3. Как определить суммарную приведенную жесткость рабочего оборудования погрузчика с гидроприводом?
4. Написать выражение суммарной приведенной жесткости последовательно и параллельно расположенных упругих элементов.
Лабораторная работа №3. Составление приведенной схемы механизма подъема грузоподъемной машины.
Задание.
1. Привести кинематическую схему и физическую модель механизма подъема.
2. Найти суммарное значение моментов инерции, приведенных к валу двигателя.
3. Найти суммарные значения моментов инерции приведенных к выходному валу редуктора, а затем – к барабану.
4. Написать выражение суммарной приведенной к грузу массы вращающихся частей привода и груза.
Рекомендуемая литература:[6], c. 91…92; [10], с.149…150
Контрольные вопросы:
1. Напишите выражения суммарных моментов инерции, приведенных к барабану.
2. Как определяется суммарная приведенная к грузу масса вращаю-щихся частей привода и груза?
3. Как определяется приведенная масса вращающихся и поступательно движущихся масс?
Лабораторная работа №4. Максимальные динамические нагрузки в элементах трансмиссии пневмоколесной машины при трогании с места.
Задание.
1. Привести динамическую схему вращающихся элементов трансмиссии пневмоколесной машины.
2. Определить суммарный (приведенный к валу двигателя) момент инерции движущихся элементов машины при разгоне.
3. Определить максимальное динамическое усилие на валу двигателя.
4. Написать выражение максимального динамического момента, нагружающего полуоси ведущих колес.
Рекомендуемая литература: [6], с.289.
Контрольные вопросы:
1. Как можно представить систему, состоящую из нескольких сосредоточенных масс?
2. Как определяется максимальное динамическое усилие на валу двигателя?
3. По какой зависимости определяется суммарный (приведенный к валу двигателя) момент инерции движущихся элементов машины при разгоне?
Лабораторная работа №5. Максимальные динамические нагрузки, воспринимаемые валом крановой тележки при разгоне.
Задание.
1. Привести кинематическую схему приводной крановой ходовой тележки.
2. Найти приведенную к ведущему колесу массу движущихся элементов тележки крана.
3. Определить максимальную динамическую нагрузку на ведущих колесах тележки.
4. Написать выражения для определения динамического момента на выходном валу редуктора и на промежуточном его валу.
Рекомендуемая литература: [6], с.288.
Контрольные вопросы:
1. Как определяют пусковой момент на валу двигателя крановой ходовой тележки?
2. Как найти избыточное усилие на ведущих колесах тележки?
3. Привести выражение для определения коэффициента динамичности нагружения ведущих колес
4. Как определяют динамический момент на выходном валу редуктора?
Лабораторная работа №6. Суммарная приведенная масса и момент инерции вращающихся частей привода двухосного колесного тягача.
Задание.
1. Привести эквивалентную динамическую схему двухосного колесного тягача.
2. Написать выражение для приведенной к ведущим колесам массы тягача.
3. Написать выражение для приведенного к ведущим колесам момента инерции движущихся элементов трансмиссии тягача.
4. Определить приведенные к валу двигателя массу и момент инерции вращающихся элементов привода.
Рекомендуемая литература: [6], с.72...76.
Контрольные вопросы:
1. Как найти суммарную приведенную к ведущим колесам массу вращающихся и поступательно движущихся элементов машины?
2. Как определить суммарный приведенный к ведущим колесам момент инерции элементов трансмиссии тягача?
3. Как определить приведенные к валу двигателя момент инерции и массу вращающихся частей привода?
Лабораторная работа №7. Жесткость упругого элемента, вводимого в металлоконструкцию бульдозера с целью предохранения его от перегрузок.
Задание
1. Определить нагрузки, возникающие при встрече бульдозера с абсолютно жестким препятствием.
2. Определить приведенную жесткость металлоконструкции бульдозера с упругим элементом.
3. Найти жесткость упругого элемента.
4. Определить наибольшую деформацию упругого элемента, вводимого в металлоконструкцию бульдозера.
Рекомендуемая литература: [2], с.153...154.
Контрольные вопросы:
1. Назовите элементы, которые могут вводиться в металлоконструкцию бульдозера для предохранения его от перегрузок.
2. Приведите формулу для определения жесткости упругого элемента.
3. Как найти общую деформацию системы «металлоконструкция – упругий элемент»?
4. Как можно определить жесткость металлоконструкции бульдозера?
5. По какой зависимости определяют наибольшую деформацию упругого элемента?
Лабораторная работа №8. Максимальная нагрузка на ходовую часть автосамосвала при падении груза на днище его кузова.
Задание.
1. Определить приведенную суммарную жесткость рессор и пневматических шин автосамосвала.
2. Найти скорость свободного падения груза.
3. Найти максимальную нагрузку на ходовую часть машины при падении груза в ее кузов.
4. Определить коэффициенты динамичности (перегрузки) для двух случаев: 1) при падении груза в кузов и 2) при плавном опускании груза в кузов.
Рекомендуемая литература: [6], с.115...116.
Контрольные вопросы:
1. Как найти скорость свободного падения груза?
2. Как определить приведенную суммарную жесткость рессор машины и ее пневматических шин?
3. По какой формуле можно определить максимальную нагрузку на рессоры машины при падении груза в кузов.
4. Как найти максимальную нагрузку на рессоры при плавном опускании груза?
Планы практических (семинарских) занятий.
Задание 1. Определение динамических параметров, приведенных к валам механизма подъема мостового крана.
Методические рекомендации. Для механизма подъема, состоящего из двигателя, двухступенчатого редуктора и барабана с грузоподъемным полиспастом определить суммарные значения моментов инерции, приведенных к валу двигателя, а также к валу барабана. Найти суммарную приведенную к грузу массу вращающихся частей привода.
Литература: [ 10 ], с. 149 …. 150.
Контрольные вопросы:
1. Каким образом в большинстве случаев учитывают малое влияние элементов привода, расположенных за двигателем?
2. Приведите правило приведения масс и моментов инерции от двигателя в сторону исполнительного органа механизма.
3. Приведите правило приведения масс и моментов инерции от исполнительного органа в сторону двигателя.
Задание 2. Определение динамических нагрузок на элементы механизма передвижения крановой тележки при пуске.
Методические рекомендации. Для механизма передвижения крановой тележки, состоящего из двигателя, муфты, редуктора и ходового колеса определить ускоряющую (избыточную) силу. Определить массу движущихся элементов, приведенную к ободу ходовых колес тележки и массу движущихся элементов механизма. Вычислить максимальное усилие, воспринимаемое механизмом при пуске, а также коэффициент перегрузки.
Литература: [4], с. 241…244
Контрольные вопросы:
1. Как определить максимальное пусковое усилие, приведенное к ободу ходовых колес?
2. По какой зависимости находят ускоряющую (избыточную) силу?
3. Напишите формулу для определения массы движущихся элементов, приведенную к ободу ходовых колес тележки.
4. По какой формуле вычисляют максимальное усилие, воспринимаемое механизмом передвижения при пуске?
5. По отношению каких усилий находят коэффициент перегрузки?
Задание 3. Определение динамических нагрузок на элементы механизма вращения и поворотную часть крана при разгоне и торможении.
Методические рекомендации. Определить суммарный приведенный (к оси вращения поворотной части) момент инерции вращающихся масс привода и поворотной части при разгоне. Найти избыточный момент на поворотной части. Рассчитать приведенные моменты инерции вращающихся масс крана и определить динамический момент, действующий на поворотную часть крана и вал двигателя. Определить приведенные выше параметры для случая торможения крана.
Литература: [6], с. 280…281
Контрольные вопросы:
1. Как находят избыточный момент на поворотной части крана?
2. По каким зависимостям рассчитывают моменты инерции вращающихся масс крана, приведенные к оси вращения его поворотной части.
3. По какой формуле определяют тормозящий момент на поворотной части крана?
4. Напишите формулу для определения динамического момента на валу двигателя при торможении.
Задание 4. Определение динамической нагрузки канатов грузоподъемной лебедки при подъеме груза «с веса» и «с подхватом».
Методические рекомендации. Для случая подъема груза «с веса» найти необходимые динамические параметры механизма подъема: приведенный к валу барабана момент инерции ротора двигателя и других элементов; массу груза, приведенную к периферии барабана и коэффициент динамичности. Для случая подъема груза «с подхватом» находят максимальную нагрузку упругого звена и коэффициент перегрузки.
Литература: [4], с. 259
Контрольные вопросы:
1. По какой формуле определяют массу груза, приведенную к периферии барабана?
2. Как найти для случая подъема груза «с веса» момент инерции ротора двигателя и других элементов, приведенный к валу барабана?
3. Напишите формулу для определения коэффициента перегрузки упругого звена для обоих случаев подъема груза.
Задание 5. Определение перегрузки канатов лифта при его пуске и торможении.
Методические рекомендации. Определить приведенные моменты инерции ротора и муфты, кабины с грузом и противовеса. Найти максимальную нагрузку грузовых канатов и канатов противовеса при пуске. Рассчитать макс.нагрузку грузовых канатов и канатов противовеса при торможении. Найти коэффициент перегрузки.
Литература: [4], с. 245…247.
Контрольные вопросы:
1. По какой формуле можно определить пусковой момент двигателя, приведенный к периферии канатоведущего шкива.
2. По каким зависимостям определяют приведенные моменты инерции противовеса и кабины с грузом?
3. Как найти максимальную нагрузку грузовых канатов при торможении?
4. Как определяют коэффициенты перегрузки для грузовых канатов противовеса лифта?
Задание 6. Расчет механизма подъема грузоподъемного крана с учетом упругости металлоконструкций.
Методические рекомендации. Составить динамическую схему подъемного механизма, размещенного на упругом основании. Составить уравнение Лагранжа для определения вынужденных колебаний системы кран-груз. Найти полное решение уравнения колебаний. Определить динамическую нагрузку на крюк и на кран. Оценить динамичность процесса подъема коэффициентами динамичности для крюка и для крана.
Литература: [1], с. 254…258
Контрольные вопросы:
1. Как определяются кинетическая и потенциальная энергии при составлении уравнения колебаний крана с грузом на крюке по уравнению Лагранжа?
2. Написать уравнение свободных гармонических колебаний данной системы в форме Лагранжа.
3. Дать оценку динамичности процесса подъема краном груза коэффициентами динамичности для крюка и крана.
Задание 7. Определение динамических параметров пластинчатого конвейера со сложной трассой.
Методические рекомендации. Выбрать тип настила и определить его ширину. Определить натяжения в характерных точках трассы. Определить расчетное натяжение тягового элемента с учетом динамического усилия. Найти расчетное натяжение тяговой цепи и выбрать ее по ГОСТу.
Литература: [5], с.168…171.
Контрольные вопросы:
1. Назовите факторы, учитываемые при выборе скорости движения полотна конвейера.
2. По какой формуле вычисляют динамическое усилие в тяговом элементе конвейера?
3. По какой зависимости определяют расчетное натяжение тяговой цепи?
4. Как определяется запас прочности тяговой цепи конвейера?
Задание 8. Определение динамических параметров скребков конвейера порционного волочения.
Методические рекомендации. Определить размеры желоба. Найти расчетные распределения масс и коэффициентов сопротивления движению ходовой части конвейера. Определить окружное тяговое усилие на приводной звездочке, расчетное натяжение тяговой цепи с учетом динамического усилия и выбрать ее по ГОСТу.
Литература: [5], с.187…190.
Контрольные вопросы:
1. На каком принципе основана работа скребковых конвейеров?
2. Приведите формулу определения динамического усилия в тяговом элементе конвейера.
3. По какой зависимости определяют коэффициент запаса прочности выбранной цепи.
Задание 9. Расчет параметров колебаний ковша драглайна на канате при внезапной его разгрузке.
Методические рекомендации. Составить уравнение движения ковша в момент его внезапной разгрузки, руководствуясь принципом Даламбера. Решить дифференциальное уравнение незатухающих колебаний порожнего ковша. Применив метод Лагранжа к случаю внезапной разгрузки ковша, найти уравнение колебаний порожнего ковша. Сравните уравнения движения ковша драглайна, полученные обоими методами.
Литература: [12], с.107…117
Контрольные вопросы:
1. В чем заключается принцип Даламбера применительно к находящейся в движении системе?
2. Приведите уравнение Лагранжа для колеблющейся системы.
3. Чему равна кинетическая энергия ковша с упряжью с учетом приведенной массы каната после внезапной его разгрузки?
Задание 10. Определение динамических нагрузок, действующих на прицепное устройство и рабочий орган скрепера Д-354 с трактором ДТ-54.
Методические рекомендации. Определить максимальную нагрузку на прицепное устройство и на рабочий орган скрепера при копании. Найти случайную нагрузку на прицепное устройство при встрече с абсолютно жестким препятствием. Определить жесткость предохранительного элемента, его упругую деформацию и сравнить ее с допустимой.
Литература: [2], с.146…149
Контрольные вопросы:
1. Приведите формулу для определения максимальной нагрузки на рабочий орган при копании в однородных грунтах.
2. Как определить случайную нагрузку на прицепное устройство при встрече с абсолютно жестким препятствием и с гранитной глыбой.
3. Как находится жесткость предохранительного элемента и его максимальная упругая деформация?
Задание 11. Определение динамических нагрузок, действующих на бульдозер Д-159 при встрече с абсолютно жестким препятствием.
Методические рекомендации. Определить максимальные случайные нагрузки при встрече отвала с абсолютно жестким препятствием: а) на рабочий орган и б) на раму трактора. Определить приведенную жесткость упругого элемента и металлоконструкции. Найти жесткость упругого элемента.
Литература: [2], с.149…152
Контрольные вопросы:
1. По каким формулам определяются максимальные нормальные нагрузки в однородных грунтах, действующие: а) на рабочий орган и б) на раму трактора?
2. Как определить коэффициенты динамичности при встрече с абсолютно жестким препятствием: а) в рабочем органе и б) в раме трактора?
3. Приведите формулу для определения приведенной жесткости упругого элемента и металлоконструкции бульдозера.
4. Как определяют необходимую жесткость упругого элемента?
Задание 12. Определение динамической устойчивости фронтального одноковшового погрузчика при движении под уклон с торможением.
Методические рекомендации. Найти нормальную реакцию на задних (по отношении к оси опрокидывания) колесах погрузчика, движущегося с торможением вниз по склону. Найти угол динамической устойчивости машины. Определить предельные значения вертикальных ускорений и перемещений погрузчика при действии на него динамических возмущений.
Литература: [6], с. 350…352
Контрольные вопросы:
1. Когда наступает граничное динамическое равновесие пневмоколесной машины?
2. Как определить нормальную реакцию на задних колесах погрузчика?
3. Как находят угол динамической устойчивости погрузчика?
4. По каким формулам определяют условия граничного динамического равновесия машины?
Задание 13. Определение максимальных динамических нагрузок трансмиссии автомобиля при трогании его с места.
Методические рекомендации. Для трансмиссии автомобиля, состоящей из двигателя, коробки передач, карданного вала, главной передачи, полуосей и ходовых колес, определить приведенный к карданному валу момент инерции автомобиля. Найти приведенные моменты внешнего сопротивления и жесткость. Определить максимальную нагрузку трансмиссии. Оценить перегрузку трансмиссии машины.
Литература: [4], с. 255…256
Контрольные вопросы:
1.По каким формулам определяют приведенные к карданному валу момент инерции и момент внешнего сопротивления автомобиля?
2.Как найти приведенную жесткость трансмиссии машины?
3.По какой формуле находят максимальную нагрузку трансмиссии?
4.Как определить коэффициент перегрузки трансмиссии?
Задание 14. Определение максимальной нагрузки рессор и баллонов грузовой автомашины при опускании груза на середину платформы.
Методические рекомендации. Определить массы груза, подрессорной и неподрессорной частей автомашины. Найти жесткости рессор и пневмабаллонов, максимальную нагрузку их. Определить максимальную нагрузку рессор. Оценить перегрузку по сравнению с постепенным нагружением того же груза.
Литература: [4], с. 265…266
Контрольные вопросы:
1. По каким зависимостям определяют массы подрессоренной и неподрессоренной частей автомашины?
2. Как определить жесткость баллонов и рессор?
3. По каким формулам находят максимальные нагрузки пневмобаллонов и рессор?
4. Как оценить перегрузку машины?
Планы занятий в рамках самостоятельной работы студентов под руководством преподавателя (СРСП)
 2015-05-06
2015-05-06 2491
2491








