Интерполяционный кубический сплайн

Рассмотрим наиболее известный и широко применяемый интерполяционный сплайн степени 3 дефекта 1. При этом будем исходить из предположения, что узлы сплайна

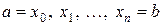(14.8)

одновременно служат узлами интерполяции, т.е. в них известны значения функции , .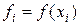

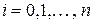Определение. Кубическим сплайном дефекта 1,интерполирующим на отрезке 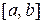данную функцию 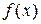, называется функция

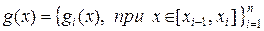, (14.9)

где

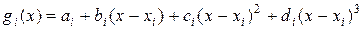, (14.10)

удовлетворяющая совокупности условий:

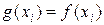– (14.11)

условие интерполяции в узлах сплайна,

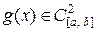– (14.12)

двойная непрерывная дифференцируемость,

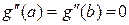– (14.13)

краевые (граничные) условия.

Заметим, что граничные условия вида (14.13) называются естественными граничными условиями.

Определенный таким образом сплайн называют еще есте­ственным или чертежным сплайном и связано это со сле­дующим обстоятельством. Желая провести плавную линию через заданные точки плоскости, чертежники фиксировали в этих точ­ках гибкую упругую рейку, тогда под влиянием упругих сил она принимала нужную форму, обеспечивающую минимум потенци­альной энергии.

Для построения по данной функции 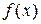интерполирующего ее сплайна (14.9) нужно найти 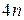его коэффициентов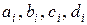

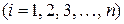
Имеем:

из условий интерполяции (14.10) для функции

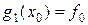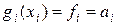, при (14.14)

из условий гладкой стыковки звеньев сплайна (14.12)

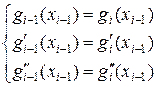, при 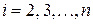(14.15)

из краевых условий (14.13)

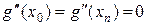(14.16)

Подставляя сюда выражения (14.9) для функций ,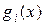

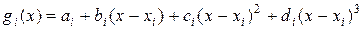
и их производных

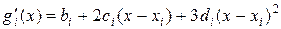(14.17)

и

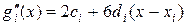(14.18)

через коэффициенты 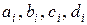при указанных значениях 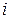и, полагая для краткости

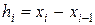, (14.19)

можно получить систему уравнений для определения неизвестных коэффициентов [ ].

Полученная система решается методом прогонки [ ].

Рассмотрим случай равноотстоящих узлов.

Тогда 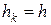и расчетные формулы для коэффициентов полинома [ ] принимают вид:

,

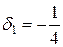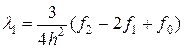
Для 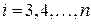вычисляем

,

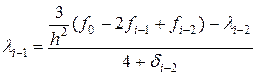
Полагаем 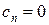и для 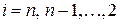вычисляем

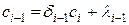
Полагаем 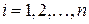и с учетом 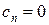получаем

,

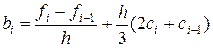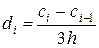
В результате при 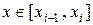значение 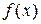можно заменить значением

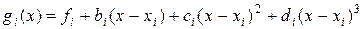
с найденными значениями коэффициентов .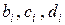

Достоинства кубической сплайн-интерполяции

· график построенной функции проходит через каждую точку мас­сива;

· конструируемая функция сравнительно легко описывается (число подлежащих определению коэффициентов равно );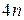

· заданным массивом построенная функция определена однозначно;

· степень многочленов не зависит от числа узлов сетки и, следова­тельно, не изменяется при его увеличении;

· построенная функция имеет непрерывные первые и вторые производные;

· построенная функция обладает хорошими аппроксимационными свойствами.

К недостаткам кубических сплайнов является то, что они склонны осциллировать в окрестностях точки, существенно отличающейся от своих соседей.