Пусть на 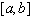 задана сетка
задана сетка 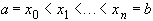 , в узлах которой известны значения функции
, в узлах которой известны значения функции  . Сплайн третьей степени
. Сплайн третьей степени 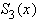 , интерполирующий заданную функцию
, интерполирующий заданную функцию 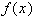 , определяется как функция, удовлетворяющая условиям:
, определяется как функция, удовлетворяющая условиям:
1) 
2) Для любого частичного промежутка 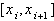
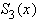 -многочлен третьей степени
-многочлен третьей степени
3) 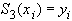
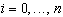
Для задания 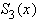 надо определить 4 коэффициента для каждого промежутка
надо определить 4 коэффициента для каждого промежутка 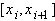 , т.е.
, т.е. 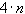 параметров.
параметров.
Условия 1) требуют чтобы во внутренних узлах сплайн и его производные до 2-го порядка были непрерывны.
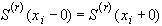
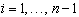
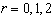
Это дает 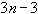 условия для определения параметров, еще
условия для определения параметров, еще 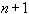 условие содержится в 3).
условие содержится в 3).
Итого имеем 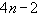 условия. Еще 2 условия, необходимые для однозначного определения сплайна, обычно задаются в виде граничных условий, т.е. условий в точках
условия. Еще 2 условия, необходимые для однозначного определения сплайна, обычно задаются в виде граничных условий, т.е. условий в точках 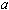 и
и 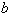 .
.
Возьмем в качестве граничных условия
4) 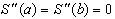
Для построения кубического интерполяционного сплайна могут быть использованы различные подходы. Проведем построение сплайна, исходя из условий 1) - 4). Из 1) и 2) следует, что??? непрерывная функция, линейная на каждом 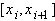 т.е.??? - линейный сплайн.
т.е.??? - линейный сплайн.
Обозначив 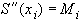 , получаем
, получаем
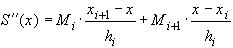 (33)
(33)
для 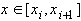 .
.
Интегрируя (5), получаем
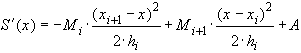 (34)
(34)
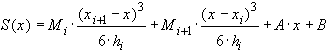 (35)
(35)
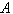 и
и 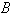 - постоянные интегрирования.
- постоянные интегрирования.
Условия 3) дают:
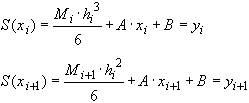 (36)
(36)
Из (36) получаем:
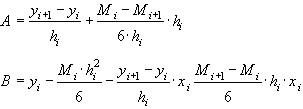
Подставляя 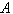 и
и 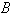 в (7), получаем:
в (7), получаем:

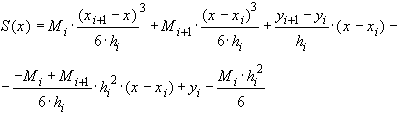 (37)
(37)
После преобразования 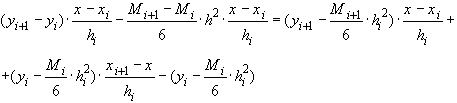
из (37) получаем
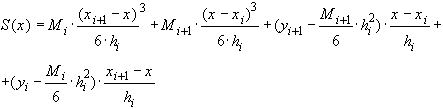 (38)
(38)
Из (34) получаем
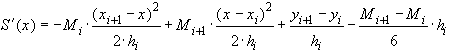 (39)
(39)
Из (39) находим односторонние пределы производной для узла 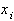 ,
, 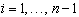
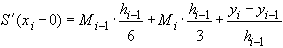 (40)
(40)
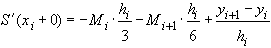 (41)
(41)
Подставляя (40) и (41) в условие непрерывности 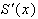 в узле
в узле 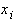 получаем:
получаем:
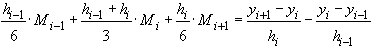 (42)
(42)
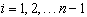
Дополняя (42) равенствами из условия 4): 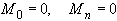 , получаем систему уравнений относительно
, получаем систему уравнений относительно 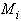 вида:
вида:
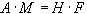 (43)
(43)
с квадратной матрицей 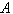 .
.
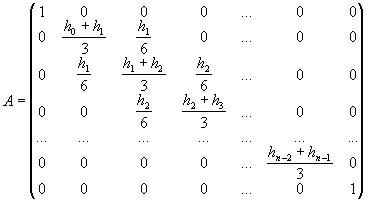
и квадратной матрицей 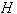
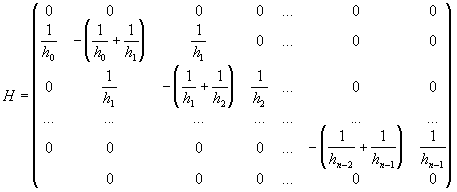
Координатами вектора 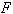 являются значения
являются значения 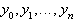 .
.
Для матрицы 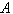 ненулевые элементы расположены на главной диагонали и двух соседних с ней. Такие матрицы называются трехдиагональными. Для
ненулевые элементы расположены на главной диагонали и двух соседних с ней. Такие матрицы называются трехдиагональными. Для 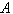 выполнено условие диагонального преобладания
выполнено условие диагонального преобладания 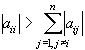 .
.
Матрица с диагональным преобладанием невырождена. Следовательно, система (42) однозначно разрешима, т.е. существует единственный кубический интерполяционный сплайн. Кроме условий 4) - условий "свободного провисания" интерполяционной кривой в точках 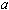 и
и 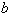 , могут быть известны наклоны интерполяционной кривой в граничных точках. Тогда условия на границах имеют вид:
, могут быть известны наклоны интерполяционной кривой в граничных точках. Тогда условия на границах имеют вид:
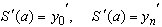 (44)
(44)
Могут быть использованы и другие варианты.
Вид граничных условий меняет некоторые элементы матрицы 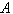 , но в любом случае она остается матрицей с диагональным преобладанием.
, но в любом случае она остается матрицей с диагональным преобладанием.
Решение системы (43) с трехдиагональной матрицей 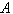 может быть найдено посредством специального варианта метода последовательного исключения неизвестных, который называется методом прогонки.
может быть найдено посредством специального варианта метода последовательного исключения неизвестных, который называется методом прогонки.
Относительно оценки погрешности и сходимости интерполяций кубическими сплайнами имеют место следующие результаты:
если 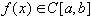 , то
, то 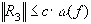 , где
, где 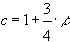 ,
, 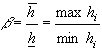 ,
,
если 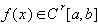 ,
, 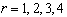 , то оценка имеет вид для
, то оценка имеет вид для 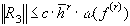 .
.
Из этих оценок следует сходимость интерполяционного процесса на последовательности сеток 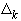 .
.
 2015-01-30
2015-01-30 538
538








