2015-04-20
1243
Пусть отрезок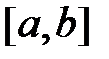 
разбит на 
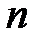частей точками 
:
.
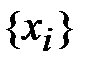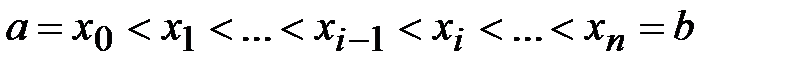Сплайном k-й степени называется функция, представляющая собой многочлен не выше k -й степени на каждом из последовательно примыкающих друг к другу интервалов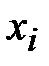 
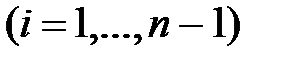. Функция непрерывна вместе со своими производными до порядка не выше k.
Например, непрерывная кусочно-линейная функция (ломаная) является сплайном первой степени с производной, терпящей разрыв в точках излома.
Пусть на отрезке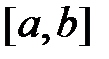 
определена функция 
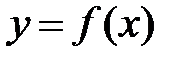, значения которой в точках 
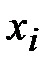равны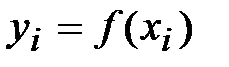 
.
Задача интерполяции функции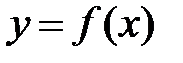 
на отрезке 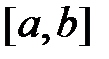кубическим сплайном (сплайном третьей степени) состоит в нахождении функции 
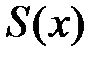, равной многочлену третьей степени 
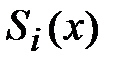на каждом отрезке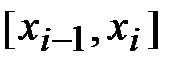 
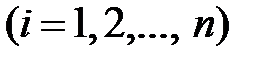, т. е.
, 
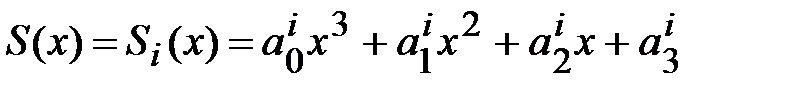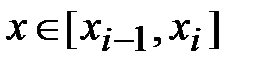, (4.3)
причем значения сплайна в узлах интерполяции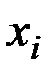 
равны соответствующим значениям заданной функции 
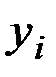и сплайн-функция непрерывна в узлах интерполяции вместе с производными первого и второго порядков:
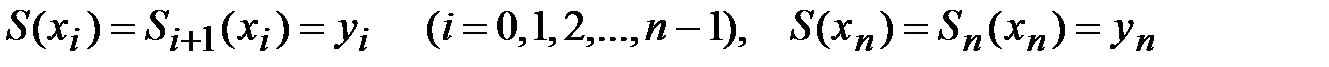, (4.4)
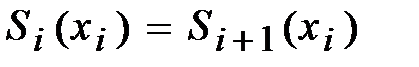, (4.5)
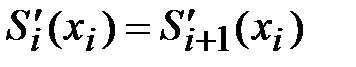, (4.6)
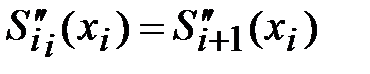. (4.7)
Условия (4.4) - (4.7) дают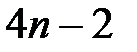 
линейных алгебраических уравнений для определения 
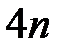неизвестных коэффициентов 
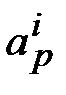(p=0, 1, 2, 3; i=1, 2,..., n) при соответствующих степенях 
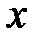в многочленах .
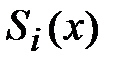Интерполяционный кубический сплайн для функции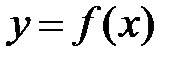 
существует и является единственным, если вместе с этими уравнениями выполняется какая-либо пара дополнительных (краевых) условий:
1. 
;
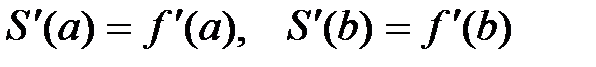2. 
;
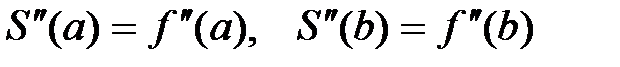3. 
.
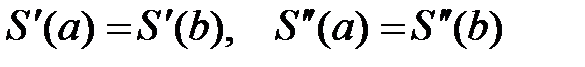Рассмотрим случай разбиения отрезка 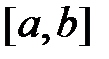на n равных частей с шагом h, для которого 
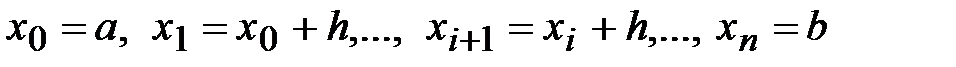и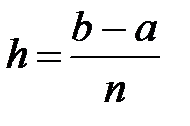 
с использованием краевых условий 1-го типа.
Введем величины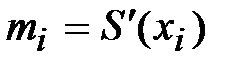 
(наклоны сплайна в точках 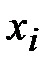(i=0, 1,..., n)).
Интерполяционный кубический сплайн вида
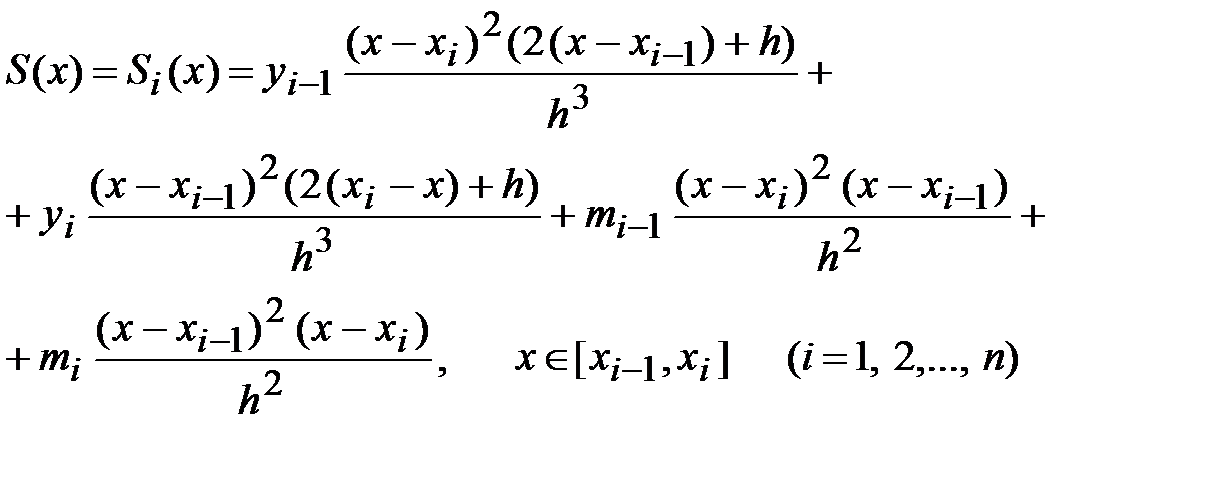(4.8) 
удовлетворяет условиям (4.4) ‑ (4.6) для любых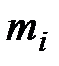 
. Из условия (4.7) и краевых условий 1-го типа можно определить n+1 параметр 
:
.
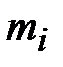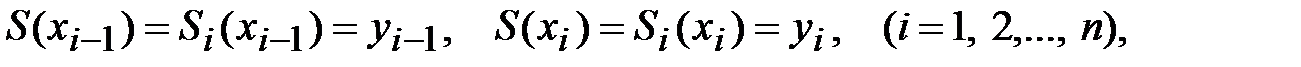
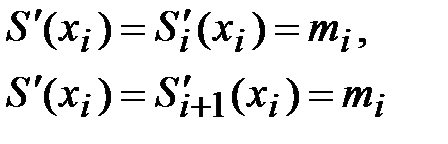
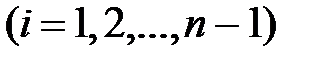Учитывая, что
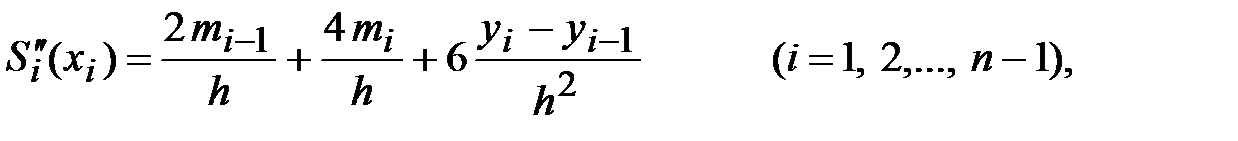
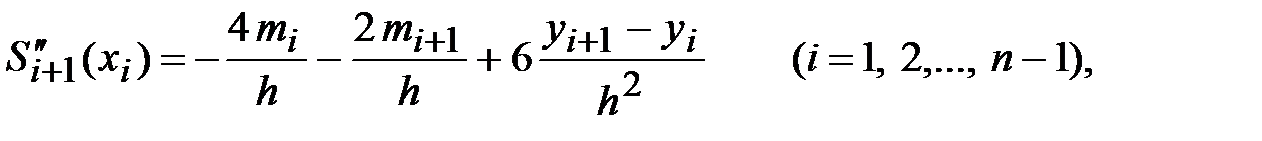
а также краевые условия 1-го типа и условия (4.7), то получим систему из n+1 линейных уравнений относительно неизвестных :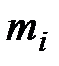
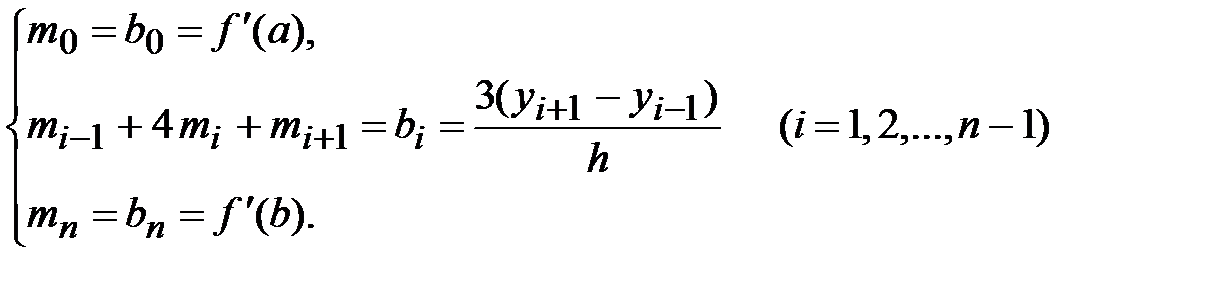(4.9)
Решение этой системы позволяет найти значения неизвестных 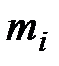и определить интерполяционный сплайн в виде соотношений (4.8). Система (4.9) может быть решена методом Гаусса или одной из его модификаций.
