Геометрические сплайны

Во многих задачах требование того, чтобы конструируемая кривая однозначно проектировалась соответственно на прямую, является слишком жестким. Расширяя допустимые классы кривых, естественно обратиться и к более общему способу описания их частичных фрагментов. В качестве нового способа задания кривых удобно использовать парамет­рический способ.

Формулировка задачи: по заданному множеству вершин

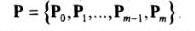
с учетом их нумерации построить гладкую кривую, которая, плавно изменяясь, последовательно проходила бы вблизи этих вершин и удовлетворяла некоторым дополнительным условиям. Эти условий могут иметь различный характер. Например, можно потребовать, что­бы искомая кривая проходила через все заданные вершины или, про­ходя через заданные вершины, касалась заданных направлений, явля­лась замкнутой или имела заданную регулярность и т. п.

При отыскании подходящего решения задачи приближения важ­ную роль играет ломаная, звенья ко­торой соединяют соседние вершины заданного набора. Эту ломаную на­зывают контрольной или опорной, а ее вершины - контрольными или опорными.

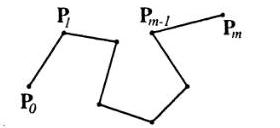
Рис. 14.2

Во многих случаях она довольно точно показывает, как будет проходить искомая кривая, что особенно полезно при решении задачи сглаживания. Каж­дая вершина заданного массива является либо внутренней либо гранич­ной (концевой). В массиве Р вершины Р₁ …, P_m-1 внутренние, а вершины Р₀ и Р_m - граничные (концевые).

Никаких ограничений на множество вершин не накладывается - они могут быть заданы как на плоскости, так и в пространстве, их взаимное расположение может быть совершенно произвольным, некоторые из вершин могут совпадать и т. д. Поэтому описание нуж­ной кривой ищут в следующем виде:

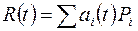(14.20)

где 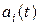- некоторые функциональные коэффициенты, подлежащие определению.

Если количество вершин в заданном множестве Р достаточно ве­лико, то найти универсальные функциональные коэффициенты, как правило, довольно затруднительно. Если универсальные коэффициенты 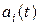все же найдены, то часто оказывается, что они наряду с нужными свойствами обладают и такими, которые не всегда удовлет­ворительно согласуются с ожидаемым поведением соответствующей кривой (например, кривая, описываемая уравнением (14.20) с этими коэффициентами, может осциллировать или заметно отклоняться от заданного множества).

Для успешного решения поставленной задачи приближения, весьма удобно привлечь кривые, составленные из элементарных фраг­ментов. В случае, когда эти элементарные фрагменты строятся по еди­ной сравнительно простой схеме, такие составные кривые принято называть сплайновыми кривыми.

Параметрические уравнения каждого элементарного фрагмента ищутся в виде (14.20) с той лишь разницей, что всякий раз привлекается только часть заданных вершин множества Р, Дтя описания элементарных кривых и вычисления их геометри­ческих характеристик (информация о которых необходима при состы­ковке) в качестве функциональных коэффициентов обычно исполь­зуются многочлены невысоких степеней. 2-й или 3-й, в первую очередь потому, что они сравнительно просто вычисляются. Наибольшее распространение получили методы конструирования составных кривых, в которых используются кубические многочлены.